| Pages:
1
..
6
7
8
9
10
..
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Bugger.
If i could do the previous bit, this bit looks a lot easier.
Perhaps a break from pure maths and back to synthesising stuff for a while ?
Over a kilo of sodium acetate is itching to become GAA thence Zinc acetate, so it can become nice clean white crystals (same as the 150g advance party
is after recrystallisation from ethanol) thence to acetic anhydride via vac distillation.
There's also this bottle o'vodka itching to become TCA, which would come in handy for catalysing some of this bottle of Turps into Turpineol ...
[Edited on 9-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Bugger.
If i could do the previous bit, this bit looks a lot easier.
Perhaps a break from pure maths and back to synthesising stuff for a while ?
|
The next few episodes are probably easier to grasp than much of what went before.
But if I build in a break now, chances are we'll never resume again... 
So let's bite the bullet!
Tomorrow: definite integrals by integrating between two boundaries. 
[Edited on 9-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Being Chain-Rule-Disabled is a bit Hampering, and we all know what happens to Hampers.
Perhaps i should just get a Maths Disabled badge and carry on regardless ?
(Free parking sounds good - i can certainly calculate that one !)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Perhaps i should just get a Maths Disabled badge and carry on regardless ?
(Free parking sounds good - i can certainly calculate that one !) |
We'll address the u-gremlins again later, then we'll see what badge fits.
The purpose of this mini-tour of calculus is mainly to understand its place in science, less to churn out integration-proficient under-graduates.
Trust me, you haven't done so bad so far. 
And u-gremlins will soon be destroyed by means of computer assisted integration, coming to you soon, HERE!
[Edited on 10-4-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
2. Eliminating C with two boundary conditions:
If F(x) + C is the integral y:
y=∫f(x)dx=F(x)+C
Now suppose we want to calculate:
Δy=y(b)−y(a)
Of course:
y(b)=F(b)+C
and:
y(a)=F(a)+C
Then:
Δy=y(b)−y(a)=F(b)+C−F(a)−C
C drops out, so:
Δy=y(b)−y(a)=F(b)−F(a)
Notation:
Δy=∫baf(x)dx=[F(x)]ba=F(b)−F(a)
We say that the function f(x) is being integrated between the boundaries x=a and x=b.
Applied example:
An object moves along a straight line with the following speed - time function:
v(t)=6t+2
Problem: What distance Δx does the object travel between t = 2 and t = 5?
We know that:
v(t)=dxdt
So:
dx=v(t)dt
dx=(6t+2)dt
Δx=∫52(6t+2)dt
The indeterminate integral of (6t+2)dt is:
∫(6t+2)dx=6×12t2+2t+C=3t2+2t+C
So:
Δx=[3t2+2t]52
\Delta x=3 \times 5^2+2 \times 5 – [3 \times 2^2 + 2 \times 2]
\Delta x= 69
Incidentally: we’ve just solved a differential equation (albeit a really simple one)!
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by aga  | Bugger.
If i could do the previous bit, this bit looks a lot easier.
Perhaps a break from pure maths and back to synthesising stuff for a while? |
If you ever want to go back to learning organic chemistry, I'm down for picking up where we left off in blog's QM/QC thread.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Darkstar  |
If you ever want to go back to learning organic chemistry, I'm down for picking up where we left off in blog's QM/QC thread. |
Me too. I've got a follow-up post ready on organo-metallics applied to Grignard reactions. But I've held back to avoid 'information overflow'... 
[Edited on 10-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Yay ! Lab time ! Woohoo !
Never stopped Sir, was just in Detention for quite a long time ...
[Edited on 10-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Any problems/questions/comments on definite integrals so far?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
(to self: Shit ! might get into Detention again ! Quick ! Think !)
No Sir.
They look fantastically clear and amazing.
I will do my homework on indefinite integrals, master that, then apply them to the Definite integrals with no difficulties at all.
(to self: add in some Sweetener or he'll Test you and you might miss the practical)
With all of the information you have kindly provided, plus all the Extra information you graciously added due to my innate dim-ness, it should all
become clear in a few days with some hard work and diligence.
(to self: he's hesistating. Get out Now !)
I must go to the bathroom Sir.
Thank you again for your patient efforts and i cannot express my gratitude enough.
(self: Exeunt stage left, running)
[Edited on 10-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Ok.
Tomorrow: two-boundary definite integrals as surface areas.
Then I'm going to bring software assisted integration forward. I was going to keep that till the end but it seems a little silly to hold back on a
method nearly everybody uses nowadays.
And then we can finally talk about differential equations proper.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Surface area under a function's curve:
It can be shown that the expression:
\int_a^b f(x)dx=\Big[F(x)\Big]_a^b
... mathematically corresponds to the green hatched area in the figure below:
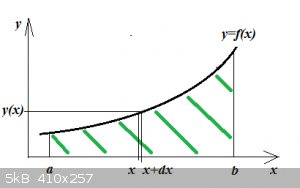
So that calculation yields the surface area contained between the curve of f(x), the x-axis and the boundaries x=a and x=b.
This can be understood somewhat intuitively as follows. Imagine a very thin slice of surface area with width dx and height y(x). Its surface area is:
dA=f(x)dx
The sum total of all these slices between a and b would the actual hatched surface area A. This is where the integration symbol:
\int
... comes from: integration between boundaries is an extended summation and the integration symbol an elongated ‘S’.
Worked example:
Determine the hatched area A for:
y=\sin x
Between:
x=0, x=\pi
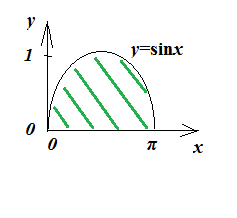
A=\int_0^{\pi} \sin x dx
A=\Big[-\cos x\Big]_0^{\pi}
A=[- \cos \pi -(-\cos 0)]=(-(-1)-0)=1
Worked physics example: Isothermal compression of an Ideal Gas, work needed.
If a volume V0 of ideal gas at pressure p0 is kept at constant temperature then according to Boyle’s Law for any other
pressure p and volume V the following relationship holds:
p_0V_0=pV
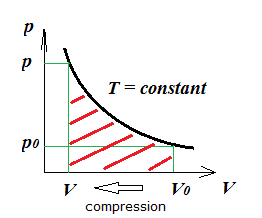
We can also write accordingly:
p(V)=p_0\frac{V_0}{V}
Thermodynamics tells us that to carry out an infinitesimally small compression dV, an infinitesimal amount of mechanical work dW has to be expended,
according to:
dW=-p(V)dV
(The negative sign is needed because dV < 0 but dW > 0)
It can be shown that for a compression from V0 to V (at constant temperature) the total amount W corresponds to the red hatched area in the
graph above, so:
W=\int_{V_0}^V (-p(V))dV
W=\int_{V_0}^V (-p_0\frac{V_0}{V})dV
W=-p_0V_0\int_{V_0}^V \frac{1}{V}dV
W=-p_0V_0\big[\ln V\big]_{V_0}^V
W=-p_0V_0(\ln V-\ln V_0)
W=-p_0V_0\ln \frac{V}{V_0}
Finally:
W=p_0V_0\ln \frac{V_0}{V}
<hr>
Simple Exercise:
Determine the value of the blue hatched area:
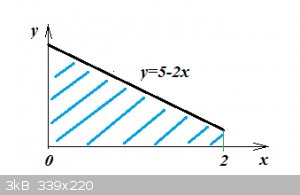
Where:
y=5-2x
with boundaries:
x=0, x=2
[Edited on 11-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
If expulsion does get discussed again, may i remind the teaching staff of the modulus of those negatives i still have in safe keeping from the 1992
school cultural visit to Paris.
You know, the ones of yourselves with 'Monsieur Fouetter la Derriere' at madame Fifi's place on the Rue de La Huchette ...
Speaking of that Blue Hatched Area clearly visible in the photos :-
y=5-2x
x=0, x=2
BHA = \int_0^2 (5-2x)dx
sum/diff rule
BHA = \Big[\int 5dx - \int 2xdx \Big]_0^2
BHA = \Big[(5x + C) - (\frac {2x^2}{2} + C) \Big]_0^2
C cancels out, 2's cancel out
BHA = \Big[5x - x^2 \Big]_0^2
BHA = (5(2) - 2^2) - (5(0) - 0^2)
BHA = (10 - 4) - (0 - 0)
BHA = 6
... although the total area in the photos seems much larger 
[Edited on 12-4-2016 by aga]
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Looking good Blogfast! Fun to see you teaching stuff I've just been learning this past year. Looking forward to seeing you go over Rotational volumes
in a week or so 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Hmm. i forgot. you're not in the 'Fifi Affair' photos.
Erm, how about the Epcot Centre 2012 photos ?
Yes. I have those too.
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Quote: Originally posted by aga  | Hmm. i forgot. you're not in the 'Fifi Affair' photos.
Erm, how about the Epcot Centre 2012 photos ?
Yes. I have those too. |
Uh, drunk...? I don't get it...
Your answers, upon quick review, are correct, but I didn't check your basic math skills at the end 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
y=5-2x
x=0, x=2
BHA = \int_0^2 (5-2x)dx
sum/diff rule
BHA = \Big[\int 5dx - \int 2xdx \Big]_0^2
BHA = \Big[(5x + C) - (\frac {2x^2}{2} + C) \Big]_0^2
C cancels out, 2's cancel out
BHA = \Big[5x - x^2 \Big]_0^2
BHA = (5(2) - 2^2) - (5(0) - 0^2)
BHA = (10 - 4) - (0 - 0)
BHA = 6
|
... is 100 % correct.  
You can also verify it by geometrical means. The area is the sum of a rectangle and a right angled triangle, both with width = 2.
The height of the rectangle is 1 (because y=5 - 2 . 2 = 1), so its area is 2 . 1 = 2.
The height of the triangle is 5 - 1 = 4, so its area is (4 . 2)/2 = 4.
The sum is 2 + 4 = 6.
[Edited on 12-4-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by The Volatile Chemist  | Looking good Blogfast! Fun to see you teaching stuff I've just been learning this past year. Looking forward to seeing you go over Rotational volumes
in a week or so  |
I wasn't going to do Rotational volumes but I'll gladly do it by special request. It's a good example of how to set up a
differential equation. 
|
|
|
The Volatile Chemist
International Hazard
    
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Haha, I'll leave it to aga/others to request it, as I've already been taught it and have three calculus textbooks at my house right now, two of which
I own. I just particularly like them because they're a nice simple example of the practical use of the integral.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Excellent result from an Excellent lecture.
(to sneaky self: attempts to insert the word Excellent into teacher's brain for writing in results)
So, where next ?
(from self: simple diversion at the point of indecision)
Oh ! It's QM/OC time.
(from self: give direction)
I do believe that's the bell.
(all: the bell rang)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
So, where next ?
(from self: simple diversion at the point of indecision)
Oh ! It's QM/OC time.
(from self: give direction)
|
The next bit you'll really like: how to compute integrals using software, on the tinkerwebs, no downloads. Hands free! 
OC/QM to resume very shortly...
[Edited on 13-4-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Integration with Wolfram Alpha’s DSolve:
The ‘computational knowledge engine’ Wolfram Alpha (WA) offers a large number of free, online mathematical tools, one of which is called DSolve.
As the name implies, DSolve is a tool for solving differential equations (DEs). Since as the simplest of DE takes on the general shape:
y’(x)=f(x)
Because:
\frac{dy(x)}{dx}=f(x)
Thus:
y(x)=\int dy(x)=\int f(x)dx
This type of DE is known as a ‘DE with separation of variables’ because all terms containing y are on one side of the equation and all
terms containing x on the other side of the equation. So we can use DSolve’s capability of solving that type of DE to compute integrals.
1. Indefinite integrals:
To have DSolve compute an indefinite integral go to WA and type the following command in the box:
DSolve[y’(x)==f(x)]
Where f(x) is a mathematical expression that is interpretable by WA. WA does not require (nor accept) LaTex but is generally very good at correctly
interpreting simply formatted mathematical expressions. Let’s try:
x\cos(3x^2-1)
Input:
DSolve[y’(x)== xcos(3x^2-1)]
This generates the following page
First and foremost, check if WA has interpreted your input correctly by checking the ‘input’ section. If the interpretation was incorrect you’ll
have to make the expression clearer (more explicit), often by adding brackets or other forms of mathematical ‘punctuation’. Note that DSolve will
also handle expressions that contain constants like a or b.
Once input is correct, scroll down for the computed integral. DSolve uses ‘c<sub>1</sub>’ as the symbol for the integration constant.
2. Definite integrals:
If the problem is a stated as:
y’(x)=f(x), f(a)=b
Where f(a)=b is the boundary (or initial) condition.
The required WA input is:
DSolve[y’(x)==f(x),y(a)==b]
Example:
y’=x\sqrt{x+1}, y(0)=0
WA input:
DSolve[y’(x)== xsqrt(x+1),y(0)==0]
Result page
Note that WA now puts the input between {} brackets because it’s a set of two equations.
In either case of definite or indefinite integrals the computed integral may superficially differ from a manual solution. That’s due to the fact
that most algebraic expressions can be written differently while returning the same function values.
Can DSolve compute any integral? Not by a long shot! As woelen pointed out, many, the majority even, of integrals do not have an
analytical solution. In plain English that means a solution cannot be obtained by means of a finite number of steps.
This problem was recognised from early on in calculus’ long history and algorithms that offer numerical solutions have been developed ever since
(the earliest recorded method is probably Euler’s Method.
WA offers its own suite for numerical integration called NDSolve and depending on interest I might spend some time on it.
[Edited on 13-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Erm, i like the Human method best.
The computers only know what we tell 'em (mostly) so MUCH better for humans to be able to do the maths instead of relying on mechanical devices.
Also, the Human programmer can make mistakes, causing the computer to give the Wrong answers (which always look Right in nicely formatted
text/graphics).
One could cite millions of pre-release tests in defence, but then so could Microsoft.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Erm, i like the Human method best.
The computers only know what we tell 'em (mostly) so MUCH better for humans to be able to do the maths instead of relying on mechanical devices.
Also, the Human programmer can make mistakes, causing the computer to give the Wrong answers (which always look Right in nicely formatted
text/graphics).
|
That's a bit of an idealistic position, aga. This is an extremely basic course.
Now imagine Big Calculus: problems that involve systems of simultaneous DEs, non-separable, perhaps second order (or higher) and non-linear.
You'd need all the help you could get, trust me!
Of course it's to be preferred to solve 'by hand' what you can (can I take this as your commitment to battle your own u-gremlins?  ) but that's not always possible. ) but that's not always possible.
Re. MS, we all like to bitch about them but would you really want to do without Excel (or similar)?
[Edited on 13-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I have no problem with Computer-Assisted.
Big problem with Computer-Enabled.
As a programmer, i have seen what happens.
(they blame the programmer as they had no way to check the computer's result)
Edit:
u-gremlin source is still being tracked.
It Will be found and assimilated.
Resistance is Futile.
Excel was not the first, but still probably the best.
[Edited on 13-4-2016 by aga]
|
|
|
| Pages:
1
..
6
7
8
9
10
..
19 |