| Pages:
1
2
3
..
19 |
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Calculus! For beginners, with a ‘no theorems’ approach!
So what really is calculus?
My preferred (but imperfect) definition:
Calculus is the study of how things change.
In this basic course we’ll concentrate on:
• Derivatives
• Differentiation
• Integrals
• Basic differential equations.
So let’s get stuck in!
The two most important functions you already knew:
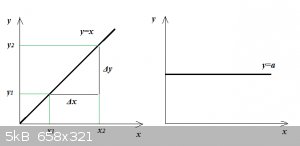
Start with the left side:
$$y=x$$
Too stupid for words really, isn’t it? For every value of x it returns that value as y.
Now notice something interesting. If I say:
$$\Delta x=x_2-x_1$$
and:
$$\Delta y=y_2-y_1$$
Then always:
$$\Delta y= \Delta x$$
Always! So that:
$$\frac{\Delta y}{ \Delta x}=1$$
Always! So what is this ratio that is always 1 for y=x? This ratio is the slope of the line. In most textbooks the term
gradient is now used instead of slope, so I’ll use it here too.
Now, it can be shown that in this particular case this gradient is the first derivative of y to x. Mathematically, if we write:
$$y=f(x)$$
Where f(x) means function of x, then:
$$[f(x)]’=y’=x’=\frac{\Delta y}{ \Delta x}=1$$
The notation:
$$[f(x)]’$$
... means the derivative of the function f(x) to x.
Another notation but meaning exactly the same is:
$$f’(x)=y’=x’=1$$
It’s an enormous step forward, even though it doesn’t look like much:
The derivative of x to x equals 1.
Now look at the function on the right hand side:
$$f(x)=y=a$$
Where a is any number. So this one’s even dumber: no matter the value of x, it always returns a!
Again there’s something interesting about it: no matter the value of Δx, always is Δy=0.
And that means our gradient:
$$\frac{\Delta y}{ \Delta x}=0$$
And by extension:
$$[f(x)]’=f’(x)=y’=a’=\frac{\Delta y}{ \Delta x}=0$$
The derivative of any number to x equals 0.
It’s important to note that obtaining the gradient of a function (and thus the derivative of f(x) to x) can only be obtained as done above
for these simple functions. For other, more complicated functions another way has to be used and we’ll soon get to that. For now I want to run with
our two main conclusions:
$$x’=1, a’=0$$
|
|
|
Metacelsus
International Hazard
Posts: 2539
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
No theorems? But theorems are so much fun! (Actually though, they are pretty interesting.)
One of my favorites: https://en.wikipedia.org/wiki/Mean_value_theorem
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
They are fun, Metacelsus but let's just say that this thread is for the theorem-averse, of which there are many. 
|
|
|
Volanschemia
Hazard to Others
Posts: 340
Registered: 16-1-2015
Location: Victoria, Australia
Member Is Offline
Mood: Pretty much all of them!
|
|
Kudos for undertaking this blogfast, I'm studying Mathematical Methods at school at the moment and what you wrote is making sense so far so I must be
doing something right!
I'm sure a lot of people will benefit from this, and I may be able to contribute if I get some spare time.
"The chemists are a strange class of mortals, impelled by an almost insane impulse to seek their pleasures amid smoke and
vapor, soot and flame, poisons and poverty; yet among all these evils I seem to live so sweetly that may I die if I were to change places with the
Persian king" - Johann Joachim Becher, 1635 to 1682.
|
|
|
JJay
International Hazard
Posts: 3440
Registered: 15-10-2015
Member Is Offline
|
|
I need to brush up on/learn differential equations, complex analysis, Fourier transforms, etc. if you get around to them.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Volanschemia  | Kudos for undertaking this blogfast, I'm studying Mathematical Methods at school at the moment and what you wrote is making sense so far so I must be
doing something right!
|
My approach will be less 'school-like' and more heuristic. One can learn in different ways.
@JJay: Thanks!
|
|
|
Maker
Harmless
Posts: 46
Registered: 1-11-2015
Member Is Offline
Mood: No Mood
|
|
Do you plan on teaching beyond what is taught in AS level maths?
Great idea for a thread, and well explained.
Just one thing to add, many (Most?) people use "d" in place of "Δ", so the derivative of x is written as dy/dx.
|
|
|
Metacelsus
International Hazard
Posts: 2539
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
Δ and d are not the same: the derivative (dy/dx) is defined (in simple terms) to be the limit as Δx approaches zero of Δy/Δx.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by Maker | 1. Do you plan on teaching beyond what is taught in AS level maths?
2. Great idea for a thread, and well explained.
3. Just one thing to add, many (Most?) people use "d" in place of "Δ", so the derivative of x is written as dy/dx. |
1. That depends on the level of interest. And whether other math lovers want to help out a bit or not.
2. Thanks!
3. You've kind of missed the point a bit. y=x and y=a are linear functions. For these:
$$\frac{\Delta y}{\Delta x}=\frac{dy}{dx}$$
That allows me to introduce the concept of the gradient without having to introduce differentials (dy and dx) just yet.
Differentials are a harder concept than intervals (Δx and Δy), at least for beginners.
Differentials will pop up in instalment 3.
As Metacelsus pointed out. Ta, MC!
[Edited on 8-3-2016 by blogfast25]
|
|
|
Maker
Harmless
Posts: 46
Registered: 1-11-2015
Member Is Offline
Mood: No Mood
|
|
1. In a later instalment, I'd be very interested to learn how to integrate or differentiate combined functions, like f(g(x)).
3. Ah yes, I see what you mean, just me trying to rush ahead  .
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by Maker | 1. In a later instalment, I'd be very interested to learn how to integrate or differentiate combined functions, like f(g(x)).
3. Ah yes, I see what you mean, just me trying to rush ahead .
|
No worries. 
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Superb stuff bloggers !
Keep this up and you'll definitely get a Sainthood.
For those of us who either didn't get more than a basic education, or went to uni and simply didn't try hard at the time, this is of enormous help.
[Edited on 8-3-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | Superb stuff bloggers !
Keep this up and you'll definitely get a Sainthood.
For those of us who either didn't get more than a basic education, or went to uni and simply didn't try hard at the time, this is of enormous help.
[Edited on 8-3-2016 by aga] |
Thanks. Sainthood? Nah. Put me out with the rest of the garbage, when I'm done...
Next instalment in about 30 mins.
Stay tuned!
[Edited on 8-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Derivation of polynomial functions:
And now for some amazing and helpful properties of derivatives.
Firstly, the product rule which relates to the derivation of the product of two function, f(x) and g(x). It states:
$$[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)$$
Let's apply it to a function:
$$u(x)=ax$$
Where a is any number.
Say:
$$f(x)=a, g(x)=x, u(x)=ax$$
Then:
$$u'(x)=a' \times x + a \times x'=0 \times x+ a \times 1= a$$
So:
$$(ax)'=a$$
How cool is that?!?!
Let's try another one:
$$u(x)=x^2= x \times x=f(x)g(x)$$
Apply the product rule:
$$u'(x)=(x^2)'=(x \times x)’=x' \times x + x \times x'=1 \times x + x \times 1=2x$$
You can apply the same method to:
$$x^3, x^4, ..., x^n$$
And you'll find:
$$(x^n)'=nx^{n-1}$$
Cool, yeah?
How about this one:
$$f(x)=ax^n$$
Then:
$$f'(x)=(ax^n)'=anx^{n-1}$$
Example:
$$f(x)=5x^3$$
$$f'(x)=15x^2$$
Secondly the sum rule, which relates to the derivation of the sum (or difference) of two function, f(x) and g(x). It states:
$$[f(x)+g(x)]'=f'(x)+g'(x)\: \text{and}\:\ [f(x)-g(x)]'=f'(x)-g'(x)$$
Nor is it limited to the sum or difference of two functions either. Take this example:
$$f(x)=2+4x-5x^4$$
With what we've learned above:
$$f'(x)=0+4-5 \times 4x^3=4-20x^3$$
Congrats! You've just learned how to calculate the derivative of a polynomial function!
A general polynomial can be defined as:
$$f(x)=a_0+a_1x+a_2x^2+ ... +a_{n-1}x^{n-1}+a_nx^n$$
Where:
$$a_0, a_1, a_2, \:\text{etc}$$
... are the polynomial's coefficients, which can be positive, negative or even zero.
The general derivative of a polynomial is, by applying what we learned above is:
$$f'(x)=a_1+2a_2x+ ... +(n-1)a_{n-1}x^{n-2}+na_nx^{n-1}$$
Now all we need is a bit of practice! I’ll let this sink in and then formulate some... exercises!
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Whoah there hoss !
$$[f(x)g(x)]'$$
In the lingo, does that mean the first derivative of a function of x multiplied by another function of x ?
Edit:
$$f(x)=a, g(x)=x, u(x)=ax$$
What does the comma operator do ?
[Edited on 8-3-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | Whoah there hoss !
$$[f(x)g(x)]'$$
In the lingo, does that mean the first derivative of a function of x multiplied by another function of x ?
Edit:
$$f(x)=a, g(x)=x, u(x)=ax$$
What does the comma operator do ?
[Edited on 8-3-2016 by aga] |
$$[f(x)g(x)]'= [f(x) \times g(x)]'$$
$$f(x)=a\:\text{and}\:\ g(x)=x,\text{then}\:\ u(x)=ax$$
Is that better for you? The comma is just a comma here (punctuation mark).
In algebra we rarely use the X sign for multiplication anymore, instead (e.g.):
$$a \times x=ax$$
Also sometimes:
$$a \times x=a.x=ax$$
The 'dot' as a symbol of a product.
[Edited on 8-3-2016 by blogfast25]
|
|
|
woelen
Super Administrator
Posts: 8012
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
An interesting addition may be:
(a*x^n)' = n*a*x^(n-1) which is valid for ANY constant power n. Also for non-integer powers and negative powers. E.g. 1/x can be written as x^(-1).
The derivative of this is (-1) * x^(-2) = -1/(x*x).
E.g. √x can be written as x^½. The derivative of this is ½*x^(½ - 1) = ½*x^(-½)=1/(2√x)
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by woelen | An interesting addition may be:
(a*x^n)' = n*a*x^(n-1) which is valid for ANY constant power n. Also for non-integer powers and negative powers. E.g. 1/x can be written as x^(-1).
The derivative of this is (-1) * x^(-2) = -1/(x*x).
E.g. √x can be written as x^½. The derivative of this is ½*x^(½ - 1) = ½*x^(-½)=1/(2√x) |
Correct. I left it implicit that n can be any number.
[Edited on 8-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Exercises: derivatives of polynomials
1.
$$-5x^4$$
2.
$$y=2-3x^4+x^6$$
3.
$$u=2+5x^{-8}$$
4.
$$v=x-2$$
5.
$$z=2-x+ax^{\pi-b}$$
... where a and b are constants.
LaTex rendering: right click on any formula. Choose ‘Show Math as > Tex commands’: a window opens that shows the code. Cut
and paste it, modify it acc. your needs and put it between double $ signs. It will now render as LaTex on SM pages (click ‘Preview Post’).
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Return to the slope, I mean: gradient!
Consider a general, smooth and continuous function f(x):
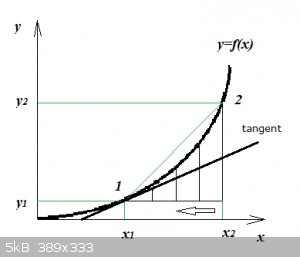
If we define intervals between points 1 and 2 as:
$$\Delta x=x_2-x_1\:\text{and}\:\Delta y=y_2-y_1$$
Then, as in the case of y=x, is:
$$\frac{\Delta y}{\Delta x}$$
... the gradient of f(x)? No. Actually, it's the gradient of the cord between point 1 and 2. It's kind of an approximate,
average gradient of f(x) between the points 1 and 2 but nowhere near accurate enough for our purpose.
Now if we move the point 2 along the curve of f(x), towards point 1, then the intervals:
$$\Delta x\:\text{and}\:\Delta y$$
... both decrease and the cord between 1 and 2 starts to resemble the line marked tangent. The tangent line is the
line that is parallel to the curve f(x) in the point 1.
The gradient of the tangent line in the point 1 is in fact the gradient of the curve of f(x) in the point 1 and by extension of what we saw in the
first instalment, that gradient is also the derivative of f(x) in point 1:
$$f'(x_1)$$
I promised as little theory as possible but a minimum is hard to avoid.
It can be shown (but I won’t do that here) that:
$$f'(x_1)=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$$
What does this mean? It means that we evaluate the expression for ever and ever smaller values of Δx, so Δx actually tends to
zero. “lim” stands for in the limit for Δx going to zero.
More explicitly written:
$$f'(x_1)=\lim_{\Delta x \to 0} \frac{f(x_1+\Delta x)-f(x_1)}{\Delta x}$$
And for the general case of x:
$$f'(x)=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}$$
It’s also written as:
$$\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\frac{dy}{dx}=y'(x)$$
Where dy and dx are so-called differentials.
Let's just try it with a simple Example: let:
$$f(x)=x^2$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{(x+\Delta x)^2-x^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{x^2+2x\Delta x+(\Delta x)^2-x^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{2x\Delta x+(\Delta x)^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{\Delta x(2x+\Delta x)}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}(2x+\Delta x)$$
$$y'(x)=2x$$
Which is what we already knew!
Going back to the differentials, we can write:
$$f'(x)=(x^2)'=\frac{dy}{dx}=2x$$
or:
$$dy=2xdx$$
The latter is in fact the first differential equation of this thread but we won’t dwell on that just yet.
Obtaining the derivatives of other functions:
In principle that same little limit ‘trick’ I performed on y=x<sup>2</sup> can be used to obtain the derivative of
any function, including non-polynomial ones. But the good news is that we don’t have to do it because other brain boxes have
already done it for us!
Plenty, plenty tables list the derivative of most functions on the Tinkerwebs. I quite like this one but by all means choose your own:
http://www.ambrsoft.com/Equations/Derivation/Derivation.htm
Note that it uses a notation we haven’t used here yet but it’s very simple. For example, what’s the derivative of cos x?
In that notation:
$$y=\cos x$$
$$y'=\frac{dy}{dx}=\frac{d}{dx}\cos x= -\sin x$$
[Edited on 10-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Derivatives, differentials and differentiation:
Good news: you already know this one! Well, basically...
We saw that the derivative of a function y can be written as:
$$y'=\frac{dy}{dx}$$
The trick now is simply to understand that:
$$dx\:\text{and}\:dy$$
... are simply variables, like x and y, and can be manipulated like them (within reason). A simple example is:
$$dy=y'dx$$
Where we've simply brought the denominator in the first equation to the left of the equation and then reversed the identity.
Remember also that we obtained the derivative y' by:
$$y'=\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\frac{dy}{dx}$$
Due to this limit taking,
$$dy\:\text{and}\:dx$$
are both infinitesimally small (but NOT actually zero). We call them also infinitesimals. That property will be very useful later, when we
start setting up differential equations for Real World problems (much later on).
For now, just look at it like this: to differentiate a function f(x), take the derivative and multiply it with dx, to obtain the differential
df(x).
Example:
$$u=3x^4+ \cos x$$
Then:
$$du=(12x^3-\sin x)dx$$
Divide both sides by dx and you've got your derivative back:
$$u'=\frac{du}{dx}=12x^3-sinx$$
Easy peasy!
|
|
|
The Volatile Chemist
International Hazard
Posts: 1981
Registered: 22-3-2014
Location: 'Stil' in the lab...
Member Is Offline
Mood: Copious
|
|
Nice to see you doing this Blogfast! I'm in Calculus 1 right now. but no theorems... I think there's a book in the library on advanced math for chemists and physicists, I had taken a peek at it a little while ago, quite
cool.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks, TVC!
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
More Rules for derivatives (and differentials):
Higher up, we saw two important rules of derivation/differentiation, the product rule and the sum/difference rule. There are two more important such
rules to master.
Firstly, the quotient rule:
If:
$$u(x)=\frac{f(x)}{g(x)}$$
Then:
$$u'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{[g(x)]^2}$$
Example:
$$u(x)=\frac{x-1}{x+1}$$
$$u'(x)=\frac{(x-1)'(x+1)-(x-1)(x+1)'}{(x+1)^2}$$
$$u'(x)=\frac{1.(x+1)-(x-1).1}{(x+1)^2}$$
$$u'(x)=\frac{x+1-x+1}{(x+1)^2}$$
$$u'(x)=\frac{2}{(x+1)^2}$$
Finally and most importantly, the Chain Rule.
Very often functions are in fact functions of other functions. A few examples should make clear what I mean:
$$\sqrt{3x^2-5}$$
$$(7+3x-x^2+2x^5)^3$$
$$\sin (2\pi x-3)$$
$$(4x^3-7x+\sqrt{x})^5$$
$$\ln \Big(\frac{3x}{x^2+5} \Big)$$
$$\large{e^{5x-\frac1x}}$$
We can write the generic form as:
$$u(x)=f[g(x)]$$
Worded: u(x) is a function f of g(x).
The Chain rule says simply:
$$u'(x)=f'[g(x)] \times g'(x)$$
This may look a little frightening but it is easier than you think. Let's try a few simple examples:
First:
$$u(x)=(3x)^5$$
$$u(x)=5(3x)^4 . (3x)'=5(3x)^4 . 3= 15(3x)^4$$
Second:
$$u(x)=\sin (2\pi x-3)$$
$$u'(x)=\cos (2\pi x-3) \times (2\pi x-3)'=2\pi \cos (2\pi x-3)$$
Third:
$$u(x)=\ln \Big(\frac{3x}{x^2+5} \Big)$$
This one's a little harder so we'll take it one step at a time. Rewrite as:
$$u(x)=\ln[f(x)]$$
Where:
$$f(x)=\frac{3x}{x^2+5}$$
So:
$$u'(x)=\frac{1}{f(x)} \times f'(x)$$
Now calculate f'(x):
$$f'(x)=\Big(\frac{3x}{x^2+5} \Big)'=\frac{(3x)'(x^2+5)-(3x)(x^2+5)'}{(x^2+5)^2}$$
$$f'(x)=\frac{3(x^2+5)-3x(2x)}{(x^2+5)^2}=\frac{3x^2+15-6x^2}{(x^2+5)^2}$$
Also:
$$\frac{1}{f(x)}=\frac{x^2+5}{3x}$$
Putting Humpty Dumpty back together again, we have:
$$u'(x)=\frac{-3x^2+15}{3x(x^2+5)}$$
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Combining the Rules and carrying out Substitutions:
In some cases several of the derivation/differentiation rules need to be applied to 'crack' a derivative.
First example:
$$y(x)=(x+1)\sqrt{\frac{x^2-3}{x^3}}$$
So what is y'(x)?
Fistly, apply the product rule:
$$\frac{d}{dx}y(x)=(x+1)'\sqrt{\frac{x^2-3}{x^3}}+(x+1)\Big[\sqrt{\frac{x^2-3}{x^3}}\Big]'$$
$$\frac{d}{dx}y(x)=\sqrt{\frac{x^2-3}{x^3}}+(x+1)\Big[\sqrt{\frac{x^2-3}{x^3}}\Big]'$$
Now we concentrate on that latter part:
$$\Big[\sqrt{\frac{x^2-3}{x^3}}\Big]'$$
Make a substitution, by calling u:
$$u=\frac{x^2-3}{x^3}$$
So we have, with the chain rule:
$$(\sqrt{u})'=\frac12 u^{-1/2}u'$$
$$u'=\frac{(x^2-3)'x^3-(x^2-3)(x^3)'}{(x^3)^2}$$
$$u'=\frac{2xx^3-(x^2-3)3x^2}{x^6}$$
$$u'=\frac{2x^2-3(x^2-3)}{x^4}$$
$$u'=\frac{9-x^2}{x^4}$$
Substituting back:
$$\Big[\sqrt{\frac{x^2-3}{x^3}}\Big]'=\frac12 \Big(\frac{x^2-3}{x^3}\Big)^{-1/2}\Big(\frac{9-x^2}{x^4}\Big)$$
Finally, substitute this back into the second equation (I'll leave that to you!)
Second example, this one a bit harder - look at this baby:
$$f(x)=[\cos (\sqrt{1+2x})]^3$$
"Take the square root of (1 + 2x), take the cosine of that value and raise the newly obtained value to the power 3".
If you're not sure how to tackle its derivative, I suggest to use the substitution method (we'll also frequently use it when we get
integrating).
Let:
$$u=\sqrt{1+2x}$$
Then:
$$f(u)=[\cos u]^3$$
Let:$$v=\cos u$$
Then:$$f(v)=v^3$$
Differentiate to v:$$d[f(v)]=3v^2dv$$
And:$$dv=(\cos u)'du$$
$$dv=-\sin u du$$
So, substituting back:
$$d[f(u)]=3[\cos u]^2(-\sin u)du=-3\sin u [\cos u]^2du$$
Now calculate du, using the chain rule:
$$du=(\sqrt{1+2x})'dx=\big((1+2x)^{1/2}\big)'dx$$
$$du=\frac12(1+2x)^{-1/2}(1+2x)'dx$$
$$du=(1+2x)^{-1/2}dx$$
Phew! Nearly there, we only need to substitute back:
$$d[f(x)]=-3\sin (\sqrt{1+2x}) [\cos (\sqrt{1+2x})]^2(1+2x)^{-1/2}dx$$
Rearrange slightly and divide both sides by dx:
$$f'(x)=-\frac{3}{\sqrt{1+2x}}\sin (\sqrt{1+2x}) [\cos (\sqrt{1+2x})]^2$$
[Edited on 19-3-2016 by blogfast25]
|
|
|
| Pages:
1
2
3
..
19 |
![[*]](images/xpblue/default_icon.gif){kind=icon}
