| Pages:
1
..
4
5
6
7
8
..
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by woelen  | | Aga, here you make a mistake. What is the derivative of xn? It is not n, but nxn-1. The integeral of n equals nx + C and not
xn + C |
Doh ! Obvious error now you point it out.
Wise words which i shall follow.
Cheers woelen
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Ok. Have a close read of my last post and see if all is clear.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Sorry, did not see that.
Must have cross posted O Praetor.
OK. Read it. Looks like some seriously heavy stuff.
(usually means that temporary interloper(s) will duck out seeing as there's heavy lifting to be done ...)
Er, the +/- thing is presumably because x^2 could be with x=-2, or +2, so the derived 4 could be from +2 or -2.
I like the 'set the hard part = one letter' bit, then substitute back later.
the 'dx' thing is confusing, mostly because i have not properly studied your earlier explanation of the various notations.
3rd example looses me when you set u = 7x and suddenly the sin() function evaporates.
Apart from that, all ready to spectacularly fail the next question !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Er, the +/- thing is presumably because x^2 could be with x=-2, or +2, so the derived 4 could be from +2 or -2.
the 'dx' thing is confusing, mostly because i have not properly studied your earlier explanation of the various notations.
3rd example looses me when you set u = 7x and suddenly the sin() function evaporates.
|
+/-:
$$\int[f(x) + g(x)]dx=\int f(x)dx + \int g(x)dx$$
or:
$$\int[f(x) - g(x)]dx=\int f(x)dx - \int g(x)dx$$
Does that clarify it?
Not really sure what you mean by the 'dx' thingy. Say you make a substitution, e.g.:
$$u=x^2-9$$
Then:
$$u'=\frac{du}{dx}=2x$$
So:
$$du=2xdx$$
And:
$$xdx=\frac12 du$$
Not sure about the sin thing:
$$\frac17 \int \sin u du=-\frac17 \cos u$$
... because the integration turns the sine into a minus cosine (as per the rules: see the table I provided).
[Edited on 29-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The +/- thing is clear now. Thankyou.
The 'meaning of d' i will probably understand better having used it a bit more.
Likely that will be the source of several errors, and soon.
sin() evaporation was just reading without brain engaged - obvious now, re-reading your text (i read it as if it were the full equation, and it
wasn't).
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Ok, I'll just post these now, just to keep you awake at night! 
Exercises:
1.
$$y=\int (3x^5-2\sqrt{x})dx$$
2.
$$y=\int 5\cos dx$$
3. (b is a constant)
$$y=\int (bx^2-4\sin x)dx$$
4. (alpha is a constant)
$$y=\int(2x-\alpha)^3dx$$
Hint: chain rule: set:
$$u=2x-\alpha$$
5.
$$y=\int x \cos(x^2-3)dx$$
Hint: chain rule: set:
$$u=x^2-3$$
6.
$$y=\int e^{2x-7}dx$$
Hint: chain rule.
7.
$$y=\int x^6\ln |x^7|dx$$
Hints:
Set:
$$u=x^7$$
and:
$$\int \ln|u|=u \ln u -u$$
8.
$$y=\int \cos(3x)[\sin(3x)]^2dx$$
Hint: set:
$$u=\sin(3x)$$
9.
$$y=\int x\sqrt{x+1}dx$$
Hint: set:
$$x=u-1$$
[Edited on 29-3-2016 by blogfast25]
[Edited on 29-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Oh bugger.
Erm, pretty please do the easiest one as an example ?
(clever trick: just 8 to do then)
Edit:
Hey ! WTF does this mean ?
$$\ln|u|$$
Parallel lines (pipe character) are new, to me, at least in maths.
Please be explainings the meanings.
[Edited on 29-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Sorry:
$$\ln|u|$$
$$|u|$$
... means the modulus of u. A modulus always returns a positive number, e.g.:
$$|3|=3$$
and:
$$|-3|=3$$
The modulus is used here because the ln of a negative number is not allowed in mathematics.
[Edited on 29-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. Cheers.
Kinda got it.
|n| = abs(n) as in the absolute value with no sign of a sign ...
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | OK. Cheers.
Kinda got it.
|n| = abs(n) as in the absolute value with no sign of a sign ... |
Yep. 'Absolute value' is another term for 'modulus'.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. Hands up.
My legs have fallen off at the first hurdle.
With 'Example 1' here http://www.sciencemadness.org/talk/viewthread.php?tid=65532&...
i don't follow how you go from
$$y=\int \sqrt{x-5}dx$$
to
$$du=(x-5)'dx=(1-0)dx=dx$$
by setting u = x - 5 .
Specifically the du = (u)'dx part.
Edit:
I mean, obviously you're processing the du thing in the second step, just that i can't see how that works later with the
$$\sqrt udu$$
part
[Edited on 30-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
$$y=\int \sqrt{x-5}dx$$
If instead the problem was:
$$y=\int \sqrt{x}dx$$
... then we could integrate it directly. But we can't because of that x - 5 bit. So we'll try and 'get rid of it' by a substitution.
Call:
$$u=x-5$$
Then:
$$u'=(x-5)'=1$$
and with:
$$u'=\frac{du}{dx} \implies du=dx$$
Now, in:
$$y=\int \sqrt{x-5}dx$$
Insert:
$$x-5=u$$
$$dx=du$$
So we get:
$$y=\int \sqrt{u}du$$
This can be integrated by power rule:
$$y=\frac23 u^{\frac32}$$
So:
$$y=\frac23 (x-5)^{\frac32}+C$$
I don't really see how much clearer to make it. Maybe more examples?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Appologies for not getting it immediately.
Definitely i need to backtrack and go over this some more, particularly the 'd' notation.
It's not your explanations at fault, just my understanding thereof, which will take some time to resolve (probably more questions too).
Basically i 'must try harder', and will do.
Edit:
so dx = (x)' ?
[Edited on 30-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Appologies for not getting it immediately.
Definitely i need to backtrack and go over this some more, particularly the 'd' notation.
It's not your explanations at fault, just my understanding thereof, which will take some time to resolve (probably more questions too).
Basically i 'must try harder', and will do. |
This isn't easy stuff. The whole thread is probably worth several months of A/GCSE level math.
So spend a little time on it (and off it) and get back when things have cleared up a bit? 
[Edited on 30-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
GCSE ?
I recall integration, trigonometry and quadratic equations from my 'O' level course aged 16.
Sadly didn't progress further than that - money was a more immediate need than qualifications at the time.
Sadder still is that i can't remember all that i learned then !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
I don’t know if this will help a lot with aga’s “d woes” but here’s an attempt to enlighten.
Look at the following figure: a smooth and continuous function y=f(x) is shown with the tangent line (red) in the point (x,y):
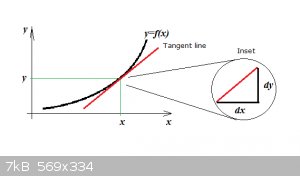
The inset shows the situation in (x,y) hugely magnified. Because of the limit taking:
$$\Delta x \to 0$$
... dx and dy are infinitesimals, very small and about as close to zero as can be imagined. But they are real numbers and we showed above that:
$$\frac{dy}{dx}=y'$$
So:
$$dy=y’dx$$
But also for example:
$$dx=\frac{dy}{y'}$$
So, dy and dx, although infinitesimally small, are ‘mathematical objects’ that can be manipulated like any other. And that is essentially what we
do when we use the substitution method.
Another example of substitution:
$$y=\int \frac{x^2}{(x^3+3)^4}dx$$
Call:
$$u=x^3+3$$
So:
$$u'=\frac{du}{dx}=3x^2$$
So:
$$du=3x^2dx$$
Also:
$$x^2dx=\frac13 du$$
Now substitute these expressions into y:
$$y=\int \Big(\frac13\Big) \frac{du}{u^4}$$
Apply the Constant Rule and rework a bit:
$$y=\frac13 \int u^{-4}du=-\frac19 u^{-4+1}=-\frac19 u^{-3}$$
So:
$$y=-\frac19 (x^3+3)^{-3}+C$$
[Edited on 31-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Amazingly that little inset of the dx / dy actually is mega helpful !
It is the difference in x and the differnce in y when those differences are almost not there.
A (brief) explanation of that there Limit Theory could be helpful here.
Specifically the notation of x -> 0 i vaguely remember meaning something like 'tending towards zero'.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Amazingly that little inset of the dx / dy actually is mega helpful !
It is the difference in x and the differnce in y when those differences are almost not there.
A (brief) explanation of that there Limit Theory could be helpful here.
Specifically the notation of x -> 0 i vaguely remember meaning something like 'tending towards zero'. |
Ok, upwards and onwards.
So I'm trying to show what:
$$y'(x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}= \lim_{\Delta x \to 0}\frac{y(x+\Delta x)-y(x)}{\Delta x}=\frac{dy}{dx}$$
... really means. Look at the picture:
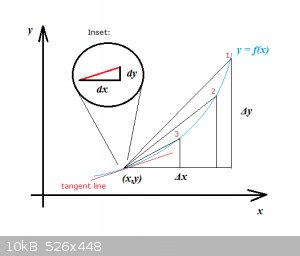
The ACTUAL gradient ( = 1st derivative) of f(x) is the gradient of the red tangent line in (x,y). y = f(x) is the blue line.
Now say we draw a chord between (x,y) and point 1. We would then calculate Δy and Δx and the ratio Δy/Δx would give us a crude
approximation of the gradient.
Now if we draw another chord between (x,y) and point 2 then notice that Δy and Δx would both decrease and the ratio Δy/Δx would be slightly better
approximation of the actual gradient.
Even smaller become Δy and Δx for a chord between (x,y) and point 3 and the ratio Δy/Δx would be yet closer to the true gradient.
It follows that if we keep reducing the size of the interval Δx, the estimate of the real gradient becomes more and more accurate and that
is the meaning of:
$$\Delta x \to 0$$
Remember that for a simple function like y = x2:
$$y'(x)=\lim_{\Delta x \to 0}\frac{y(x+\Delta x)-y(x)}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{(x+\Delta x)^2-x^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{x^2+2x\Delta x+(\Delta x)^2-x^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{2x\Delta x+(\Delta x)^2}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0}\frac{\Delta x(2x +\Delta x)}{\Delta x}$$
$$y'(x)=\lim_{\Delta x \to 0} (2x +\Delta x)$$
$$y'(x)=2x$$
Finally, the required incantation: 'gremlins, gremlins, go away, don't come back another day' 
[Edited on 2-4-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Integration by parts:
In addition to the rules above there’s another popular integration technique that bears mentioning, called integration by parts.
A slightly different way of writing the derivation product rule, with u and v both functions of x is:
$$d(uv)=udv+vdu$$
Integrating both sides we get:
$$\int d(uv)=uv=\int udv+\int vdu$$
Or:
$$\int udv=uv-\int vdu$$
This format is useful to integrate certain types of integrals. A classic example is:
$$\int xe^xdx$$
Set:
$$dv=e^xdx$$
Integrate to get v (ignore the integration constant for now):
$$\int dv=v=\int e^xdx=e^x$$
Then set:
$$u=x$$
So:
$$du=dx$$
Now plug it all in:
$$\int xe^xdx=xe^x-\int e^xdx=xe^x-e^x+C=(x-1)e^x+C$$
Another example:
$$\int x \cos(ax)dx$$
Set:
$$dv=\cos(ax)dx$$
Integrate:
$$v=\frac1a \sin(ax)$$
Then:
$$u=x$$
$$du=dx$$
$$\int x\cos(ax)dx=\frac{x}{a} \sin(ax)-\int \frac1a \sin(ax)dx=\frac{x}{a} \sin(ax)-\frac1a \int \frac1a \sin(ax)dx$$
$$\int x\cos(ax)dx=\frac{x}{a} \sin(ax)+\frac{1}{a^2}\cos(ax)+C$$
And with C just a constant, we can rework slightly to:
$$\int x\cos(ax)dx= x\sin(ax)+\frac{1}{a}\cos(ax)+C_1$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So, if it's just 'applying the rules', with immense trepidation, the Exercises ...
1. (cribbed from teach)
$$y=\int (3x^5-2\sqrt{x})dx$$
Sum/difference rule
$$y=\int 3x^5dx - \int 2 \sqrt{x}dx$$
Constants rule
$$y=3 \int x^5dx - 2 \int \sqrt{x}dx$$
Power rule, left hand side
$$y=3 \frac {x^6}{6}+C - 2 \int x^{\frac 12}dx+C$$
Roll the constants into one, Power rule Right hand side
$$y=\frac {3x^6}{6} - 2 \big ( \frac {x^{\frac 32}}{\frac 32} \big)+C$$
Simplify fraction left hand side, flip fractional divisor right hand side
$$y=\frac {x^6}{2} - \frac 43 x^{\frac 32}+C$$
2.
$$y=\int 5\cos dx$$
$$y=5 \int \cos dx$$
$$y=5 \sin x + C$$
3.
$$y=\int (bx^2-4\sin x)dx$$
Sum/difference rule
$$y=\int bx^2dx - \int 4 \sin(x)dx$$
Constants jobbie
$$y=b \int x^2dx - 4 \int \sin(x)dx$$
Power rule, roll constants together
$$y=b \frac{x^3}{3} + 4 \cos(x) + C$$
Simplify
$$y=\frac{bx^3}{3} + 4 \cos(x) + C$$
4.
$$y=\int(2x-\alpha)^3dx$$
set $$u = 2x-\alpha$$
$$y=\int u^3dx$$
Power rule
$$y= \frac {u^4}{4}+C$$
Return to the 'real meaning of u'
$$y= \frac {(2x -\alpha)^4}{4}+C$$
5.
$$y=\int x \cos(x^2-3)dx$$
set $$u = 2x +3$$
$$y=\int x \cos(u)dx$$
$$y=x\int \cos(u)dx$$
$$y=-x \sin(u)$$
$$y=-x \sin(x^2-3)$$
Here, and in exercise 6, the chain rule is simply not understood yet. so i got to go back and see how that all works again.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
1, 2 and 3 are correct. The problems start with the substitutions.
Let's see if the following can make you see the problem.
Another, more intuitive way of understanding integration by substitution:
Let’s take a simple example:
$$y=\int \cos x dx$$
The part:
$$\cos x$$
... is called the integrand ("cosine of x"), the part:
$$dx$$
... is called the differential ("the differential of x"). Note that in both cases we have "... of x". In that case we can simply
integrate directly:
$$y=\sin x +C$$
Now what happens if we change the integrand to:
$$\cos (5x)$$
So:
$$y=\int \cos (5x)dx$$
Now the integrand is "cosine of 5x" and the differential "the differential of x". Note: "... of 5x" and "... of x".
They don't 'match': this cannot be integrated directly. To try and resolve this problem, we carry out a substitution:
$$u=5x$$
So:
$$du=(5x)'dx=5dx$$
So:
$$dx=\frac15 du$$
Substitute all this into the integral:
$$y=\int \cos(u) \frac15 du=\int \frac15 \cos (u) du=\frac15 \int \cos (u) du$$
Now the integrand is "cosine of u" and the differential "differential of u", so now we can integrate directly:
$$y=\frac15 \sin (u)$$
Substitute back and add integration constant:
$$y=\frac15 \sin (5x)+C$$
Second example:
$$y=\int (4x+5)^{\frac13}dx$$
Again, the integrand ("cubic root of 3x+5") does not 'match' the differential ("differential of x").
Substitute:
$$u=4x+5$$
$$du=(4x+5)'dx=(4+0)dx=4dx$$
$$dx=\frac14 du$$
So:
$$y=\int u^{\frac13} \frac14 du=\frac14 \int u^{\frac13}du$$
Now the integrand and differential 'match' and the integral can be integrated directly:
$$y=\frac14 \times \frac34 u^{\frac43}$$
$$y=\frac{3}{16}(4x+5)^{\frac43}+C$$
[Edited on 4-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
erm, so the bits before the dx have to be 'simple' as in no operators like +,-/sin,tan etc or you got to substitute those bits before integrating ?
To be honest, it's all rather more difficult with Integration than it was with derivatives.
The concepts are still not 100% clear, although the way to perform the computations are.
The dx/dy are still hanging about causing mischief gremlin-wise.
Perhaps i'm at the limit of my brain capacity.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Look at it like this.
We saw that:
$$\int \cos(5x)=\frac15 \sin(5x)+C$$
Integration is the anti-operator of derivation, so the derivative of:
$$\frac15 \sin(5x)+C$$
... should give us the starting function cos(5x). So:
$$(\frac15 \sin(5x)+C)'=\frac15 (\sin(5x))'+0$$
$$=\frac15 \cos(5x)(5x)'=\frac15 \times 5 \cos(5x)$$
$$=\cos(5x)$$
... which proves the integration was correct.
But had we not put the factor:
$$\frac15$$
... upfront, the result would not have been correct. W/o the substitution we would have missed that factor.
Same for:
$$y=\frac{3}{16}(4x+5)^{\frac43}+C$$
Derive:
$$y'=\frac{3}{16}\big[(4x+5)^{\frac43}\big]+0$$
$$=\frac{3}{16} \times \frac43 (4x+5)^{\frac13}(4x+5)'$$
$$=\frac14 (4x+5)^{\frac13} (4+0)$$
$$y'=(4x+5)^{\frac13}$$
[Edited on 4-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The bit that i'm still failing to understand is the dx/dy thing, so a step backwards is required.
e.g.
$$y=\int (x-1)dx$$
... is still gobeldygook. Does it mean that
$$\frac {dy}{dx} = (x-1)$$
therefore
$$dy = (x-1)dx$$
and if
$$\int dy = y$$
meaning that if
$$\int dy = \int (x-1)dx$$
and if int(dy) actually does equal y ...
$$y=\int (x-1)dx$$
?
Applogies again : this must be like pulling teeth from a titanium robo-donkey.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
All that is correct.
And yes:
$$\int dy=y, \int dx=x, \int du=u, \int dv =v,\:\text{etc, etc}$$
Because integration is the opposite of differentiation, it 'cancels' the differentiation.
Another segment to follow tonite...
[Edited on 5-4-2016 by blogfast25]
|
|
|
| Pages:
1
..
4
5
6
7
8
..
19 |