| Pages:
1
2
3
4
..
19 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by chemrox  | Calculus courses are all about the notation. I never cared for the limit notation or the Δ forms. I like the Liebenetz dy/dx format. Of course you
have to explain what they mean..and calculus is the only way to learn trig
dy/dx ≠ Δy/Δx
|
I have to disagree somewhat here. Notation is mainly conventional. Some prefer Leibniz, others Newton ("dot y"):
$$\dot{y}=\frac{dy}{dx}$$
Using calculus professionally, one has little choice but to familiarise oneself with the various notations and variations. It's a bit like musical
notation: it may differ slightly from one composer to another but most will be able to read another's scribblings w/o problems.
As regards limit notation, do you have an alternative?
As regards "dy/dx ≠ Δy/Δx", that case has been firmly made higher up.
|
|
|
j_sum1
Administrator
       
Posts: 6354
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
There are reasons why both leibniz' dy/dx notation and Newton's f'(x) notation have both survived.
Newton's notation simplifies and manipulates nicely. f'(x) simplifies to f'. f''(x) simplifies to f''. This easily enables f to be manipulated as
an algebraic object.
Newton's notation also enables substitution into the function to be shown easily. f(2), f(x), f(t), f(n+3), f(g(x)) and so forth.
Leibniz emphasises the concept of a rate better. It allows for separation of the two differentials which is useful for integration and solving
differential equations. (In Leibniz notation, integration is more than just antidifferentiation -- it is a sum to find an area. Conceptually, this
is different and it shows in the notation.)
Leibniz is also useful in that it shows the variable that one is differentiating with respect to. dy/dx and dy/dz and so forth. To my knowledge,
Newton's applications were differentiating with respect to time only. Leibniz easily allows multi-variable functions and partial differentials.
∂2y/∂x∂z for example.
There are advantages to both notations and a good understanding of calculus is aided by having facility with both.
|
|
|
chemrox
International Hazard
    
Posts: 2961
Registered: 18-1-2007
Location: UTM
Member Is Offline
Mood: LaGrangian
|
|
I'm not seeing a lot of the material you drew. I'm looking at in firefox. Any idea what might be the issue? What format were you putting the math in?
"When you let the dumbasses vote you end up with populism followed by autocracy and getting back is a bitch." Plato (sort of)
|
|
|
j_sum1
Administrator
       
Posts: 6354
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
I didn't draw anything. My post is all text.
Bloggers is using latex -- as described here.
|
|
|
chemrox
International Hazard
    
Posts: 2961
Registered: 18-1-2007
Location: UTM
Member Is Offline
Mood: LaGrangian
|
|
Quote: Originally posted by blogfast25  | Quote: Originally posted by chemrox  | Calculus courses are all about the notation. I never cared for the limit notation or the Δ forms. I like the Liebenetz dy/dx format. Of course you
have to explain what they mean..and calculus is the only way to learn trig
dy/dx ≠ Δy/Δx
|
I have to disagree somewhat here. Notation is mainly conventional. Some prefer Leibniz, others Newton ("dot y"):
$$\dot{y}=\frac{dy}{dx}$$
Using calculus professionally, one has little choice but to familiarize oneself with the various notations and variations. It's a bit like musical
notation: it may differ slightly from one composer to another but most will be able to read another's scribblings w/o problems.
As regards limit notation, do you have an alternative?
As regards "dy/dx ≠ Δy/Δx", that case has been firmly made higher up.
|
I see what you mean. The problem I'm having is I'm not seeing it all so please disregard earlier comments. Except for one thing: I would not bother
with any theory. You can take analysis if you want to really learn it. If you want to use calculus, professionally or otherwise, jump to the Liebniz
(thanks for the spelling) notation. I would however name the rules. For example I think you started out with the product rule. I think naming the
rules is a good memory crutch. As far as notations go maybe its a good idea to cover them all right away. I went to a big school where every math
prof. liked a different text. It drove me nuts until I found one I liked in the library to carry me through. Linear algebra was the same way. When I
took it I found the text was the barrier and I found a 67 page one that covered the course. That course was about making good guesses about series
more than anything.
"When you let the dumbasses vote you end up with populism followed by autocracy and getting back is a bitch." Plato (sort of)
|
|
|
chemrox
International Hazard
    
Posts: 2961
Registered: 18-1-2007
Location: UTM
Member Is Offline
Mood: LaGrangian
|
|
I had to reload my browser. Now about 2/3 of the pages are gone WTF? Did all the latex disappear?
"When you let the dumbasses vote you end up with populism followed by autocracy and getting back is a bitch." Plato (sort of)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
No, I can see all of it. Looks like a browser problem at your end.
[Edited on 19-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
When a derivative becomes zero...
Consider the following smooth and continuous generic function y=f(x):
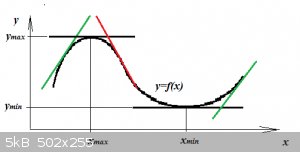
I’ve also drawn the tangent lines in various points, in green where the tangent has a positive gradient, in red where the tangent has a
negative gradient.
As we move from left to right the positive gradient first becomes smaller and smaller, to reach zero at the top of the ‘hill’ (black tangent is
horizontal).
Moving beyond that point the gradient of the tangent line becomes negative, then less and less negative to reach zero at the bottom of the
‘valley’ (black tangent is horizontal). It then becomes positive again.
The points where the tangent line’s gradient becomes zero are called optima (minimum and/or maximum) and are the points are those
for which:
$$y’(x_{max})=0\:\text{and}\:y’(x_{min})=0$$
So optima occur where:
$$y’=\frac{dy}{dx}=0$$
Parabola:
An interesting case in point is the quadratic polynomial:
$$y=ax^2+bx+c$$
Graphically it shows as a parabola:
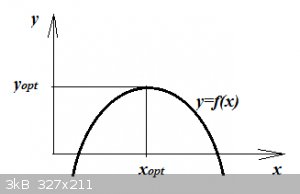
Since as:
$$y’=2ax+b$$
There always is an optimum for:
$$2ax+b=0$$
$$x_{opt}=-\frac{b}{2a}$$
The value of y<sub>opt</sub> can be calculated from plugging into y.
Note that here the optimum is a maximum but parabolas that exhibit a minimum also exist of course (just flip the graph over 180
degrees).
This property of derivatives becoming zero where optima of the function f(x) exist is used in optimisation problems (next up).
[Edited on 19-3-2016 by blogfast25]
|
|
|
woelen
Super Administrator
        
Posts: 8051
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
Yet another notation used for d/dx is simply D. The operator D is a linear functional with the property Df = f'
Powers of D are used to represent repeated differentiation, e.g. D²f = DDf = D(f') = f''.
Integration can be written as 1/D or D-1, e.g. D-1f stands for the integral of f(ξ)dξ from ξ=0 to ξ=x.
Using this notation, one can even use fractional powers, e.g. D½x = 2√x/√π
And of course repeating D½ two times yields D½D½ = D, which simply is taking the first derivative.
The operator D can also be used as argument of (analytic) functions, e.g. eD (here e is the base of the natural logarithm, the number
2.7182818....) and this thing can be applied as operator to functions, e.g.
[eaD]f(x) = f(x+a) for any function f and any constant a.
Here eaD is not a function, but a functional.
[Edited on 19-3-16 by woelen]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
And related to the operator Del, is the nabla:
$$\nabla=\Big(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\Big)$$
and:
$$\nabla^2$$
But I think we're starting to 'show off', as this thread is mainly intended for the education of the calculus-impaired. 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Oh dear.
Late for class again. What is going on ?
Latex, derivatives and nablas !
Might have to copy someone's homework. Anybody ? Please ?
Maybe i can get away with trying out some Latex ...
$$aga_{sober}=-\frac{bloggers_{drunk}}{0}$$
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
$$=-\infty$$
You tryin' to tell me somethang, mistah? 
So, what can we do by way of... ermm... remedial classes?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Erm, reading the thread, it all looks a bit over my head.
The Rules thing kinda suggests that despite the 'orrible algebraic complexity, some Genii have worked out some easy-to-apply rules that basically make
it a lot simpler if you just follow those rules.
Is that right, or did i just imagine an easy way ?
[Edited on 20-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Yes, that's definitely what they're there for: make derivations easier.
Do you have problems with these:
http://www.sciencemadness.org/talk/viewthread.php?tid=65532#...
Send answers by U2U, if you prefer. 
[Edited on 20-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
No, because i'm amazing and am so incredibly awesome that i can eat peanuts ... and my mom has a car ! etc etc.
Honest answer : Yes.
I have not got a Clue how you would even attempt those questions, despite reading, printing, then re-reading your erstwhile explanations.
Add-ups, take-aways, times-bys, share-bys, basic algebra, and possibly some trigOhNometry : they are all OK, as in i understand most of those, i.e.
had a basic education.
|
|
|
yobbo I
Harmless

Posts: 8
Registered: 20-3-2016
Member Is Offline
Mood: No Mood
|
|
Keep your socks pulled up there blogfast. There is some serious competition out there!
https://www.coursera.org/learn/calculus1?siteID=.GqSdLGGurk-...
Thanks for the bit about the infitesmals, never knew that or unstood when they were moved about.
[Edited on 20-3-2016 by yobbo I]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Add-ups, take-aways, times-bys, share-bys, basic algebra, and possibly some trigOhNometry : they are all OK, as in i understand most of those, i.e.
had a basic education. |
Ok. If you want to carry on with this 'course', you'll have to 'help me, help you'. I don't understand well enough what causes you to struggle with:
$$y=ax^n$$
Ergo:
$$y'=(ax^n)'=a(x^n)'=a \times nx^{n-1}=anx^{n-1}$$
Maybe try and explain better what you're struggling with? Here or by U2U?
Thanks.
[Edited on 21-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I;m still staring at these http://www.sciencemadness.org/talk/viewthread.php?tid=65532#... and wonding what to do.
If you could work through example 1, that would be enormously helpful.
|
|
|
j_sum1
Administrator
       
Posts: 6354
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
Ok. These are easy. You ca manage them aga.
Drop the power by one.
The new coefficient is the old coefficient multiplied by the old power.
Repeat for each term in the polynomial.
So, if
$$y= 3x^5 + 2x^3 - 9x^2 + 6x +11$$
$$y'=15x^4 + 6x^2 -18x +6$$
The x is infact x^1. It degenerates to x^0 on differentiating. x^0 is of course 1 and so you are left with the coefficient only.
The constant term is a term in x^0. This degenerates to zero on differentiating. There are multiple ways of thinking that through. It is worth
pausing to think that one through carefully and convince yourself as to why.
As so often happens, it is the so-called easy ones that are tricky because something simplifies out of sight and the notation starts to alter.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
OK.
Ex. 1:
Derive:
$$(-5x^4)'$$
As -5 is a constant we put it upfront (proof: product rule):
$$(-5x^4)'=-5(x^4)'$$
To derive x4, put the exponent 4 upfront, then reduce the exponent by 1:
$$(x^4)'=4x^3$$
Put it all back together:
$$(-5x^4)'=-5(x^4)'=-5(4x^3)=-20x^3$$
Ex. 3:
$$u=2+5x^{-8}$$
This is a sum, so the derivative is the sum of the derivatives that make up the sum:
$$u'=(2)'+(5x^{-8})'$$
$$(2)'=0$$
$$(5x^{-8})'=5(x^{-8})'=5(-8x^{-9})=-40x^{-9}$$
$$u'=0-40x^{-9}=-40x^{-9}$$
Ex. 5: (the hardest one)
$$z=2-x+ax^{\pi-b}$$
This is a sum (and a difference) of three terms. Derive each term individually, then add them up again:
$$(2)'=0$$
$$(x)'=1$$
$$(ax^{\pi-b})'=a(x^{\pi-b})'=a[(\pi-b)x^{\pi-b-1}]=a(\pi-b)x^{\pi-b-1}$$
Adding up:
$$z'=-1+a(\pi-b)x^{\pi-b-1}$$
<hr>
Recapping:
1. The derivative of a constant (a) equals zero:
$$(a)'=0$$
2. The derivative of x equals 1:
$$(x)'=1$$
3. Constant rule:
$$(af(x))'=af'(x)$$
4. Power rule:
$$(x^n)'=nx^{n-1}$$
5. Sum rule:
$$[f(x)+g(x)]'=f'(x)+g'(x)$$
6. Product rule:
$$[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x)$$
(we'll recap the quotient rule and the chain rule again, later)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thank you, j_sum1.
|
|
|
woelen
Super Administrator
        
Posts: 8051
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
Another thing which may help making it more easy to remember is to combine the product rule and chain rule in order to derive the quotient rule. No
need to memorize the quotient rule.
[f(x)/g(x)]' can be written as [f(x)u(x)]', where u(x) = 1/g(x).
Now apply the product rule:
[f(x)u(x)]' = f'(x)u(x) + f(x)u'(x)
Next, apply the chain rule for deriving the derivative of u(x) = 1/g(x). Here, 1/g(x) can be written as h(g(x)), with h(x) = 1/x.
[h(g(x))]' = h'(g(x))g'(x).
h'(x) = -1/x2, hence h'(g(x)) = -1/[g(x)]2, hence u'(x) = -g'(x)/[g(x)]2
Now we have all in place to express [f(x)/g(x)]' in terms of f(x), g(x), f'(x) and g'(x):
f'(x)u(x) + f(x)u'(x) = f'(x)/g(x) - f(x)g'(x)/[g(x)]2
Taking everything under the same denominator we get
[f(x)/g(x)]' = [f'(x)g(x) - f(x)g'(x)]/[g(x)]2
-----------------------------------------------------
The only way to make it really is easy is doing/exercising it. Just take derivatives of many different functions and soon you'll see that you
naturally apply the product rule and chain rule correctly. I never felt the need to memorize the quotient rule.
Practice, practice and practice!
[Edited on 21-3-16 by woelen]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Many thanks for taking the trouble to show the workings.
i think i got it !
If i did understand it , then Excercise 2 should go like this ...
$$y=2-3x^4+x^6$$
$$y'=0-3(4x^3)+6x^5$$
$$y'=6x^5-12x^3$$
Semantics difficulties : How do you actually say these two, and what is the difference ?
$$f'(x)$$
$$f(x)'$$
First derivative of function f ?
Edit:
Exercise 4 should go like :-
$$v=x-2$$
$$v'=1-0=1$$
[Edited on 21-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Yup, history in the making: first successful derivations (2) by aga on SM! Lift off but we probably need a bit more 'lift' to come.
$$f'(x)=f(x)'=(f(x))'=[f(x)]'$$
... Are all synonymous and can all be used. I prefer f'(x): "the (first) derivative of the function f of x".
Woelen is right on all counts and as with all things, practice makes perfect! So I'll bring on some more specifically chosen examples tonight.
As you've guessed we're now all ganging up on you and further resistance is futile. You're in a corner: either hoist the white flag or fight your way
out of it! We WILL teach you some calculus, whether you like it or not, hombre!
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Um, it looked a lot harder : a LOT harder.
Sorry for the prevarication.
Edit:
Is a Green flag OK ?
Just the hanky got used and it's a bit icky now.
[Edited on 21-3-2016 by aga]
|
|
|
| Pages:
1
2
3
4
..
19 |