| Pages:
1
..
14
15
16
17
18
19 |
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Flow of a fluid between parallel plates:
This is an interesting problem because of how the differential equation is set up.
We have two very large parallel plates, both stationary. Between them a Newtonian fluid flows in one direction. From prior art we can expect the
velocity profile u(y) to look like this:
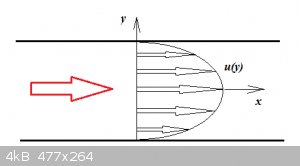
Now we consider a slice of fluid with thickness Δy:
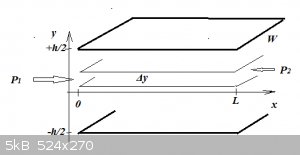
To derive u(y) we first note that there is no acceleration, only uniform motion:
$$\frac{\partial u}{\partial t}=0$$
This means acc. Newton's second law that the balance of forces acting on a slice of moving fluid of thickness Δy must be zero::
$$\Sigma F_x=0$$
The forces acting on the slice are:
1. P<sub>1</sub>ΔyW and P<sub>2</sub>ΔyW. This pressure difference is of course the driving force for the flow.
2. Two shear forces (top and bottom): LWσ(y) and LWσ(y+Δy).
The balance of forces is:
$$P_1\Delta y W-P_2\Delta y W+LW[\sigma(y+\Delta y)-\sigma(y)]=0$$
Rearranged slightly:
$$\frac{\Delta P}{L}=-\frac{\sigma(y+\Delta y)-\sigma(y)}{\Delta y}$$
Take the limit to get a derivative:
$$\frac{\Delta P}{L}=-\lim_{\Delta y \to 0}\frac{\sigma(y+\Delta y)-\sigma(y)}{\Delta y}$$
$$\frac{\Delta P}{L}=-\frac{d\sigma}{dy}$$
The shear stress for a Newtonian fluid is:
$$\sigma=\mu\frac{du}{dy}$$
Plugged in we get:
$$\frac{\Delta P}{L}=-\mu\frac{d^2u}{dy^2}$$
This is a simple second order differential equation which on integration gives:
$$u=-\frac{\Delta P}{2\mu L}y^2+c_1y+c_2$$
c<sub>1</sub> and c<sub>2</sub> are integration constants, the values of which are obtained by applying the following boundary
conditions:
$$y=-\frac{h}{2} \implies u=0, y=+\frac{h}{2} \implies u=0$$
Plugging in the values for c<sub>1</sub> and c<sub>2</sub> we get:
$$u=\frac{\Delta Ph^2}{2L\mu}\Big[\frac14-\Big(\frac{y}{h}\Big)^2\Big]$$
For y = 0, we get:
$$u_{max}=\frac{\Delta Ph^2}{8L\mu}$$
For a infinitely long plates we can optionally write:
$$\frac{\Delta P}{L}=\frac{\partial P}{\partial x}$$
Now we need to find the average velocity
$$\bar{u}$$
from:
$$\bar{u}=\frac{1}{h}\int_{-h/2}^{+h/2}u(y)dy$$
This yields:
$$\bar{u}=\frac{\Delta Ph^2}{12L\mu}$$
And so with a substitution:
$$\large{u(y)=6\bar{u}\Big[\frac14-\Big(\frac{y}{h}\Big)^2\Big]}$$
[Edited on 15-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thread table of content:
Introduction to gradients
Derivation of polynomials
Defining the gradient more accurately
Derivatives, differentials and differentiation
More rules for derivation (and differentiation)
Combining the rules and carrying out substitutions
When a derivative becomes zero (optima)
Optimisation problems
Integration (“anti-derivation”)
Basic rules of integration (indefinite integrals)
Integration by parts
The definite integral
Integration between two boundaries
Surface are under a function’s curve
Integration with Wolfram Alpha’s DSolve function
Simple differential equations
Train stopping problem
Hot Coffee: no need to blow on it!
Syphon: tank emptying time
Hydrogen generator (student problem)
Projectile velocity problem
Partial derivatives
Multi-variate optima
Famous second order DEs
Simple Harmonic Oscillator
The Schrödinger Equation
The Heat Equation
Cooling fin: steady state
Experimental determination of heat conductivity k
Flow between two parallel plates
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
WiFi woes?
The field strength of a WiFi signal in a house is governed by the Helmholtz Equation (here in two dimensions):
$$\nabla^2E+\frac{k^2}{n^2}E=f(x,y)$$
Where E is the signal strength, k the wave number of the used radiation and n the refractive index of the (x,y)
space to that radiation. f(x,y) is the source function of the radiation.
$$\nabla^2E=\frac{\partial^2E}{\partial x^2}+\frac{\partial^2E}{\partial y^2}$$
If the (x,y) space is sub-divided into:
$$N\times M$$
... grid points, then the signal strengths can be calculated from a giant system of equations of the form:
$$\frac{E(i+1,j)+E(i-1,j)-2E(i,j)}{\Delta x^2}+\frac{E(i,j+1)+E(i,j-1)-2E(i,j)}{\Delta y^2}+\frac{k^2}{n(i,j)^2}E(i,j)=f(i,j)$$
i and j are the index numbers of the grid points.
Here's a fellow who did just that (and more!)
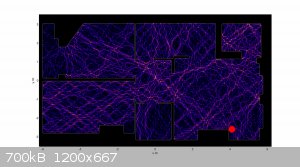
Look at the complicated room plan, the position of the (red point) WiFi source and the tendrils of 'internet goodness' as they snake through the
available space!
The link also points to a related Android app by the same author.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The plot looks nice.
A overlaid plot of the signal in the reverse direction would be interesting.
(internet, as with all meaningful communications, is a two-way thing).
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
I wouldn't know about that: I'm IT averse.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Second order DEs (continued):
We've seen a few examples of 2nd order DEs, now let's have a slightly more systematic glimpse into simple equations of the form:
$$ay''+by'+cy=0 \:\text{where}\:y=f(x)$$
These are known as 2nd order linear homogeneous DEs (with constant coefficients).
We're obviously looking for a solution function that doesn't really change form even after two derivations.
We propose something like (where the suffix p stands for 'particular'):
$$y_p=e^{\lambda x}$$
Derive:
$$y_p'=\lambda e^{\lambda x}=\lambda y_p$$
and again:
$$y_p''=\lambda^2 e^{\lambda x}=\lambda^2y_p$$
Plug these into the original DV:
$$a\lambda^2y_p+b\lambda y_p+cy_p=0$$
The yp drop out and we're left with:
$$a\lambda^2+b\lambda +c=0$$
This is known as the Characteristic Equation. As a quadratic equation it suggests there are two λ meeting that condition:
Example:
$$y''-y'-6y=0\:\text{where}\:y=f(x)$$
With boundary conditions:
$$y(0)=0,y'(0)=5$$
Characteristic equation:
$$\lambda^2-\lambda-6=0$$
which has two Real roots:
$$\lambda=+2, \lambda=-3$$
A theorem (which will remain untreated here) now tells that the Good solution of the DE is a linear combination, as follows:
$$y=c_1e^{2x}+c_2e^{-3x}$$
To prove this works, let's find the integration constants c1 and c2 from the boundary conditions:
$$y(0)=c_1+c_2=0$$
and:
$$y'=2c_1e^{2x}-3c_2e^{-3x}$$
$$y'(0)=2c_1-3c_2=5$$
Together these equations now yield:
$$c_1=+1,c_2=-1$$
So the full solution of the original DE is:
$$y=e^{2x}-e^{-3x}$$
You can now prove the validity of this solution by plugging it into the original DV.
<hr>
That was all kind of easy because the roots of the Characteristic Equation were both Real.
Next time we'll see what happens when that's not the case.
[Edited on 19-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Speak for yourself !
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Which part did you find hard?
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
$$y_p=e^{\lambda x}$$
$$y_p'=\lambda e^{\lambda x}=\lambda y_p$$
The e^x bit basically.
Natural logs in general.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | $$y_p=e^{\lambda x}$$
$$y_p'=\lambda e^{\lambda x}=\lambda y_p$$
The e^x bit basically.
Natural logs in general.
|
$$e=2.71828...$$
Example:
$$e^3=(2.71828)^3=20.0855$$
In general:
$$e^x, e^{ax}, e^{\lambda x}$$
... are all simple exponential functions (a and λ are Real numbers).
Derivation rule (chain rule applies here):
$$(e^{\lambda x})'=e^{\lambda x}\times (\lambda x)'=\lambda e^{\lambda x}$$
So, if:
$$y_p=e^{\lambda x}$$
$$y_p'=\lambda e^{\lambda x}=\lambda y_p$$
$$y_p''=\lambda^2 e^{\lambda x}=\lambda^2y_p$$
Natural logarithm: the anti-function of ex:
Say if:
$$\ln a=b$$
Then:
$$e^b=a$$
Example:
$$\ln (20.0855)=3$$
Because:
$$e^3=20.0855$$
[Edited on 19-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Bollocks! That sodding Chain Rule !
So, if i can ever get even close to 'getting it'. the function of x is
$$\lambda x$$
and the function of the function of x is
$$e^{\lambda x}$$
hence, following derivative chain rule :
$$(e^{\lambda x})'=e^{\lambda x}\times (\lambda x)'$$
Why is it not a Single un-chained function of x, where
$$f(x) = (e^{\lambda x})$$
?
Edit:
Is it as simple as the fact that x gets times by lambda = one function, then raising 'e' by the result of that function constitues another function ?
[Edited on 19-5-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | Bollocks! That sodding Chain Rule !
So, if i can ever get even close to 'getting it'. the function of x is
$$\lambda x$$
and the function of the function of x is
$$e^{\lambda x}$$
hence, following derivative chain rule :
$$(e^{\lambda x})'=e^{\lambda x}\times (\lambda x)'$$
Why is it not a Single un-chained function of x, where
$$f(x) = (e^{\lambda x})$$
?
Edit:
Is it as simple as the fact that x gets times by lambda = one function, then raising 'e' by the result of that function constitues another function ?
[Edited on 19-5-2016 by aga] |
You're basically correct.
The Chain Rule formally is as follows:
If f is a function of g(x), so:
$$f[g(x)]$$
Then:
$$\big[f[g(x)]\big]'=\frac{df(x)}{dx}=\frac{df(g(x))}{dg(x)} \times \frac{dg(x)}{dx}$$
Much shorter:
$$f(g)\:\text{where}\:g=g(x)$$
Then:
$$\frac{df}{dx}=\frac{df(g)}{dg} \times \frac{dg(x)}{dx}$$
In the example at hand:
$$g(x)=\lambda x$$
$$f=e^{g(x)}=e^{\lambda x}$$
It also happens to be that for exponential functions:
$$\frac{d(e^g)}{dg}=e^g$$
For example:
$$\frac{d(e^x)}{dx}=e^x$$
The e-functions are unique in that respect.
So:
$$f'=e^{\lambda x} \times (\lambda x)'= e^{\lambda x} \times \lambda=\lambda e^{\lambda x}$$
<hr>
Tomorrow: another approach to the chain rule. So hold fire, Hombre!
[Edited on 20-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Let’s try and smash those chain gremlins that seem to be wound tightly around your bollocks for once and for all (w/o smashing the bollocks
themselves)
Where you wrote:
| Quote: Originally posted by aga |
So, if i can ever get even close to 'getting it'. the function of x is
$$\lambda x$$
and the function of the function of x is
$$e^{\lambda x}$$
|
... you’ve got the right idea. Knowing what to do with the chain rule boils down to identifying the ‘master function’ (f!) and
the ‘subordinate’ one (g!). This is of course a metaphor, not to be taken literally.
Then we’ll derive the ‘master’ first, then the ‘subordinate’ one.
But forget about the derivation for a minute. For now we’ll concentrate on what, in an actual function, plays the part of f and
what plays the part of g.
Here are some examples:
1.
$$f=\sqrt{x^2+5}$$
$$g=x^2+5$$
$$f(g)=\sqrt{g}$$
2.
$$f=(2\ln x+8)^{1/3}$$
$$g=2\ln x+8$$
$$f(g)=g^{1/3}$$
3.
$$f=e^{3x^2}$$
$$g=3x^2$$
$$f(g)=e^g$$
Exercises: using the same method and format determine f(g) in the following cases.
1.
$$f=\cos(3\sqrt{x}+7)$$
2.
$$f=\ln \Big(\frac{1}{1+x}\Big)$$
3.
$$f=[\cos (2x)+3]^4$$
4.
$$f=\sqrt [5]{1-2x}$$
5.
$$f=\sin\Big(\ln x+\frac{1}{x^2}\Big)$$
6.
$$f=\sqrt [3] {2x^4-x^2-3}$$
[Edited on 20-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
aga, are you interested in solving your chain rule problem or did you not see the previous post? 
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
sorry. didn't see it. will start now.
(so much random shizzle piles up so fast these days).
[Edited on 22-5-2016 by aga]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
1.
$$f=\cos(3\sqrt{x}+7)$$
$$g=3\sqrt{x}+7$$
$$f=\cos(g)$$
2.
$$f=\ln \Big(\frac{1}{1+x}\Big)$$
$$g=\frac{1}{1+x}$$
$$f=\ln (g)$$
3.
$$f=[\cos (2x)+3]^4$$
$$g=\cos (2x)+3$$
$$f=g^4$$
4.
$$f=\sqrt [5]{1-2x}$$
$$g=1-2x$$
$$f=\sqrt [5]g$$
5.
$$f=\sin\Big(\ln x+\frac{1}{x^2}\Big)$$
$$g=\ln x+\frac{1}{x^2}$$
$$f=\sin(g)$$
6.
$$f=\sqrt [3] {2x^4-x^2-3}$$
$$g=2x^4-x^2-3$$
$$f=\sqrt [3] g$$
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Well, these were all 100 % correct, showing you have no problem seeing which is the 'master' and which is the 'subordinate' function.
To derive we now apply the Chain Rule. For my examples so far we had:
1.
$$f=\sqrt{x^2+5}$$
$$g=x^2+5$$
$$f=\sqrt{g}$$
2.
$$f=(2\ln x+8)^{1/3}$$
$$g=2\ln x+8$$
$$f=g^{1/3}$$
3.
$$f=e^{3x^2}$$
$$g=3x^2$$
$$f=e^g$$
<hr>
The Chain Rule says:
$$\frac{df}{dx}=\frac{df}{dg}\times \frac{dg}{dx}$$
So let's apply it to these examples:
1.
$$\frac{df}{dg}=(\sqrt{g})'=\frac12g^{-1/2}=\frac{1}{2\sqrt{x^2+5}}$$
(Edit: changed 'x' to 'g')
$$\frac{dg}{dx}=(x^2+5)'=2x+0=2x$$
$$\implies \frac{df}{dx}=\frac{df}{dg}\times \frac{dg}{dx}=f'(x)=\frac{2x}{2\sqrt{x^2+5}}=\frac{x}{\sqrt{x^2+5}}$$
2.
$$\frac{df}{dg}=(g^{1/3})'=\frac13 g^{-2/3}=\frac{1}{3g^{2/3}}=\frac{1}{3(2\ln x+8)^{2/3}}$$
$$\frac{dg}{dx}=(2\ln x+8)'=2\frac{1}{x}+0=\frac{2}{x}$$
$$\implies f'(x)=\frac{df}{dg}\times \frac{dg}{dx}=\frac{2}{3x(2\ln x+8)^{\frac23}}$$
3.
$$\frac{df}{dg}=\big(e^g\big)'=e^g=e^{3x^2}$$
$$\frac{dg}{dx}=(3x^2)'=3(x^2)'=3(2x)=6x$$
$$\implies f'(x)=6xe^{3x^2}$$
<hr>
Note that for very simple composite functions of the form (where a is a constant):
$$f(ax)$$
... the chain rule also becomes very simply:
$$f=(ax)^n \implies f'=an(an)^{n-1}$$
$$f=\cos(ax) \implies f'=-a\sin(ax)$$
$$f=\sin(ax) \implies f'=a\cos(ax)$$
$$f=e^{ax} \implies f'=ae^{ax}$$
<hr>
Now smash the chain gremlins and apply the Chain Rule to the previous exercises!
'Cheatsheet':
http://www.ambrsoft.com/Equations/Derivation/Derivation.htm
[Edited on 23-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Almost boiled the noodles with this one :
$$\frac{df}{dg}=(\sqrt{x})'=\frac12g^{-1/2}=\frac{1}{2\sqrt{x^2+5}}$$
I am HOPING it should read :
$$\frac{df}{dg}=(\sqrt{g})'=\frac12g^{-1/2}=\frac{1}{2\sqrt{x^2+5}}$$
If not, this rocket mission might not miss Mars, and actually hit it, which would be an environmental disaster.
Assuming a typo, i'll now Baldly go where no Baldy has gone before ...
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
AAAAaaaarrghh!!! TERRIBLE typo alert. Harakiri being contemplated now. 
[Edited on 23-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
1.
$$f=\cos(3\sqrt{x}+7)$$
$$f=cos(g)$$
$$g=3\sqrt{x}+7$$
1st derivative should be :
$$(\cos(3\sqrt{x}+7))'.(3\sqrt{x}+7)'$$
$$= -sin(3\sqrt{x}+7).(3x^{\frac 12}+7)'$$
$$= -sin(3\sqrt{x}+7).\frac 32 x^{-\frac 12}$$
Fiddle with just to get sqrt instead of fractional powers
$$= -sin(3\sqrt{x}+7).\frac 3{2 \sqrt x}$$
Then go crazy just to confuse bejeesus out of everyone, including myself :
$$= \frac {-3sin(3\sqrt{x}+7)}{2 \sqrt x}$$
Better pause there for a second to see if it's going OK or has all ballsed up already.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The Emperor banned seppuku quite some time ago, so you may not.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
1. is entirely correct. Well done.
5 to go.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Phew!
Beer load a bit high to attempt more right now.
Will certainly mangle the rest tomorrow a.m.
Out of interest, which form did you end up with as the 'correct' answer ?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
All last three expressions were 100 % and merely 'synonymous'.
The last one would be my 'aesthetically' preferred one.
Often the preferred version is decided on by what you'll do with it afterwards.. A first derivative is rarely the end of solving a real
problem.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
2.
$$f=\ln \Big(\frac{1}{1+x}\Big)$$
$$g=\frac{1}{1+x}$$
$$f=\ln (g)$$
$$\ln \Big(\frac{1}{1+x}\Big)'.\Big(\frac{1}{1+x}\Big)'$$
$$=(1+x).\Big(\frac{1}{1+x}\Big)'$$
Some head scratching with
$$\Big(\frac{1}{1+x}\Big)'$$
first by power rule :
$$\Big(\frac{1}{1+x}\Big)' = \Big((1+x)^{-1}\Big)' = -1(x+1)^{-2} = \frac {2}{-1(x+1)} = -\frac{2}{x+1}$$
But it is also kinda chainy, so :
$$g=(x+1), f=\frac 1g$$
$$\Big(\frac{1}{1+x}\Big)'.(x+1)'$$
(x+1)' = 1 so that will come out the same. Back to the Question :
$$-\frac{2}{x+1}.(x+1) = -\frac {2(x+1)}{x+1} = -2$$
|
|
|
| Pages:
1
..
14
15
16
17
18
19 |
![[*]](images/xpblue/default_icon.gif){kind=icon}
