| Pages:
1
..
12
13
14
15
16
..
19 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Don't feel too bad - it was way over my head from the start !
At this point, i can now follow large chunks of what is shown, which is Vast improvement.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Hope you pass! 
Quote: Originally posted by aga  |
At this point, i can now follow large chunks of what is shown, which is Vast improvement. |
At least that's a modest achievement, for both of us! 
[Edited on 6-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
You are very much understating your achievements.
2 years ago i knew nothing of chemistry, quantum mechanics, higher maths or bodily hygiene.
Maths, Physics and Chemistry are great, although a few words on bodily hygiene would be helpful.
I very much hope that Others follow your lectures, and i really wish more people would join in.
Perhaps they would if i didn't smell so bad.
Edit:
Of course TVC will Pass !
A bit shy, but very bright indeed.
[Edited on 6-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Well, I'll put that feather in my cap then.
And I continue thoroughly, nay: streneously, to deny any involvement with any bodily thingymejibs of whatever kind. 
[Edited on 6-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Oh well, back to OC then to discover the identities of the highly active aromatics in my armpits ...
The IUPAC name is probably 1,2,3,GottaPukeNow-o-PassOut.
Edit:
Some progress already ! I predict an isomer:
1,4,Gag-o-Run, 2-Puke, 3-b'jeysus, which is clearly a lachrymator.
[Edited on 6-5-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Tomorrow and Sunday, to the joy of the many and sadness of the few, what will be kind of the 'final' instalments, these on the Heat Equation.
After that and depending on demand, some random questions, answers, exercises etc into which this thread will peter out. To oblivion and beyond!
[Edited on 6-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Demand.
^^^ Look- it's already there.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Heat Equation (one dimension only):
Consider a straight rod of length L, constant cross-section A, made of a homogeneous material of density ρ, heat capacity c<sub>p</sub>
and heat conductivity k.
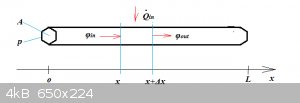
At some point we start heating (or cooling) a section of the rod. This creates a dynamic situation: temperature T will now depend on position x, as
well as time t:
T=f(x,t)
Before deriving the DV that describes the phenomenon, two more definitions are needed:
φ(x,t) is the heat flux (W/m<sup>2</sup> inside the rod due to heat
conduction. inside the rod due to heat
conduction.
Q(dot)(x,t) is the heat input (or sink) per unit of volume per unit of time. We’ll keep Q(dot) a little vague for now, as its actual form will
depend strongly from problem to problem.
To set up the DV, we set up the heat balance of an element of length Δx:
A\rho c_p \Delta x \frac{\Delta T}{\Delta t}=Aφ(x)-Aφ(x+\Delta x)+ A\Delta x \dot{Q}
Divide both sides by AΔx and rearrange slightly:
\rho c_p\frac{\Delta T}{\Delta t}=-\frac{φ(x+\Delta x)-φ(x)}{\Delta x}+\dot{Q}
Now take the limit of both sides to get derivatives:
\rho c_p \lim_{\Delta t \to 0} \frac{\Delta T}{\Delta t}=-\lim_{\Delta x \to 0}\frac{φ(x+\Delta x)-φ(x)}{\Delta x}+\dot{Q}
\rho c_p\frac{\partial T}{\partial t}=-\frac{\partial φ}{\partial x}+\dot{Q}
Looks ‘pretty’ perhaps but it isn’t very useful: we need to eliminate φ(x,t). To do so we use Fourier’s law on heat conduction:
φ(x)=-k\frac{\partial T}{\partial x}
Insert into the previous equation:
c_p\rho \frac{\partial T}{\partial t}=-\frac{\partial}{\partial x}\Big(-k\frac{\partial T}{\partial x}\Big)+\dot{Q}(x,t)
c_p\rho \frac{\partial T}{\partial t}=k\frac{\partial^2T}{\partial x^2}+\dot{Q}(x,t)
Call κ (kappa) the heat diffusivity:
\kappa=\frac{k}{c_p\rho}
\frac{\partial T}{\partial t}=\kappa \frac{\partial^2T}{\partial x^2}+\frac{\dot{Q}(x,t)}{c_p\rho }
After some time of constant heating (or cooling) a steady state will have been achieved, where T(x,t) will no longer depend on t, so:
\frac{\partial T}{\partial t}=0
The heat equation then reduces to the steady state version:
\kappa \frac{d^2T}{dx^2}+\frac{\dot{Q}(x,t)}{c_p\rho }=0
<hr>
Next up: two applications of the heat equation.
[Edited on 7-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
We still have not done limit theory yet, have we ?
How does one 'take the limit' ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
No, because this thread is a 'theorem free zone' (kind of), remember? 
But we have seen the basics.
In essence, is we have a function f(x), then limit theory tells us:
\lim_{\Delta x \to x}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{df(x)}{dx}=f'(x)
For simple functions limit taking is easy. Take e.g. f(x) = 3x<sup>2</sup> - 4.
\frac{[3(x+\Delta x)^2-4]-[3x^2-4]}{\Delta x}
=\frac{3(x^2+2x\Delta x+\Delta x^2)-4-3x^2+4}{\Delta x}
=\frac{3x^2+6x\Delta x+3\Delta x^2-3x^2}{\Delta x}
=\frac{\Delta x(6x+3\Delta x)}{\Delta x}
=6x+3\Delta x
\Delta x \to 0
\implies 6x=\frac{df(x)}{dx}
Which is correct, as we know.
For more complicated functions, limit taking can be a lot harder, though...
[Edited on 7-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Looks fairly hard with what (to You) is a simple example !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quick reminder of what is a derivative: definition of linear velocity
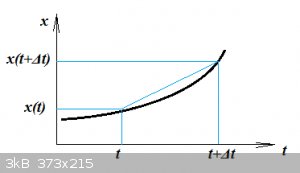
An object travels along an x-axis. At time t its position is x(t) and some time Δt later it is x(t+Δt).
Between these two points the average velocity would be:
v_{av}=\frac{\Delta x}{\Delta t}=\frac{x(t+\Delta t)-x(t)}{\Delta t}
But the True velocity is found by:
v(t)=\lim_{\Delta t \to 0}\frac{x(t+\Delta t)-x(t)}{\Delta t}=\frac{dx}{dt}
Halleluyah!
[Edited on 7-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
This limit taking lark, as in the heat equation set up, lies at the heart of setting up many DVs.
Take this simple example of a tank emptying itself through a bottom hole:
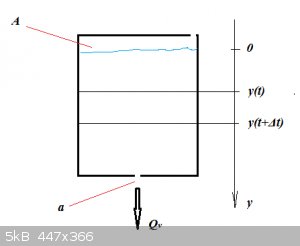
The tank with constant cross-section A and a sharply cut bottom hole of cross-section a obeys Torricelli's law (inertias assumed
zero), so that volumetric rate through the bottom hole is:
Q_v=a\sqrt{2gh}
In a time interval Δt the height of fluid in the tank changes by:
\Delta y=y(t+\Delta t)-y(t)
That's a volume ΔV (negative sign is needed because ΔV is negative):
\Delta V=-A\Delta y
Divide by Δt:
\frac{\Delta V}{\Delta t}=-A\frac{y(t+\Delta t)-y(t)}{\Delta t}
Take the limit for Δt to 0, so we get:
\frac{dV}{dt}=-A\frac{dy}{dt}
This is of course another expression for Q<sub>v</sub>, so:
-A\frac{dy}{dt}=a\sqrt{2gy}
From this DV the total emptying time can then be calculated by integration.
[Edited on 8-5-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Very clever having a hole in the top of the tank at the top right hand side.
I suspect the equations would be a bit more complex otherwise !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Very clever having a hole in the top of the tank at the top right hand side.
I suspect the equations would be a bit more complex otherwise ! |
Yes. Pressure above the water would be dropping, reducing throughput.
If p0 is atmospheric pressure and V0 the volume of air in the tank at the start, then with Bernoulli and the Ideal Gas Law:
\frac{v^2}2+\frac{p_0}{\rho}=gy+\frac{p_0V_0}{\rho(V_0+Ay)}
\frac{v^2}2=gy+\frac{p_0V_0}{\rho(V_0+Ay)}-\frac{p_0}{\rho}
\frac{v^2}2=gy+\frac{p_0V_0}{\rho(V_0+Ay)}-\frac{p_0(V_0+Ay)}{\rho(V_0+Ay) }
\frac{v^2}2=gy-\frac{p_0Ay}{\rho(V_0+Ay)}
\frac{v^2}2=\frac{\rho gy(V_0+Ay)-p_0Ay}{\rho(V_0+Ay)}
\frac{v^2}2=\frac{[\rho g(V_0+Ay)-p_0A]y}{\rho(V_0+Ay)}
Q_v=a\sqrt{2\frac{[\rho g(V_0+Ay)-p_0A]y}{\rho(V_0+Ay)}}
-A\frac{dy}{dt}=a\sqrt{2\frac{[\rho g(V_0+Ay)-p_0A]y}{\rho(V_0+Ay)}}
Whether that's even analytically integratable remains to be seen! 
<hr>
An additional consideration is needed here. In order for liquid to be able to flow out of the opening, the pressure on the tank side must always be
higher than on the other side:
\frac{p_0V_0}{V_0+Ay}+\rho g y>p_0
The point where steady flow would stop is:
y=\frac{p_0A-\rho g V_0}{\rho gA}
Beyond that point, liquid would still be trying to leave and air trying to enter at the same time. This is what happens when you try and empty a full
bottle of liquid by turning it up-side down!
[Edited on 8-5-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Cooling fin: Steady State
A cooling fin is attached to a wall at T0, surrounded by a fluid at T∞:
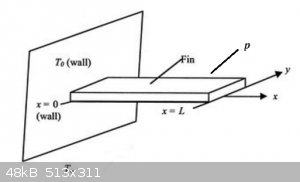
We assume steady state and heat loss by convection only. For a segment of length Δx, convection heat loss is acc. Newton:
- p\Delta xh(T-T_{\infty})
(p is the perimeter of the fin, for a slab e.g. p = 2 x width + 2 x thickness)
The heat balance of that segment now is:
A\rho c_p \Delta x \frac{\Delta T}{\Delta t}=Aφ(x)-Aφ(x+\Delta x)- p\Delta xh(T-T_{\infty})
Deriving as for the general heat equation and for steady state, we obtain:
\frac{\partial^2T}{\partial x^2}-\frac{ph}{kA}(T-T_{\infty})=0
Solution:
Firstly a simple substitution:
\tau=T-T_{\infty}
\implies d\tau=dT,d^2\tau=d^2T
And call:
m^2=\frac{ph}{Ak}
Plugging into the DV:
\tau''-m^2\tau=0
This a linear, second order homogeneous DV and its solution is of the general form:
\boxed{\tau=c_1e^{mx}+c_2e^{-mx}}
Where c1 and c2 are two integration constants. We find these by applying the boundary conditions.
1st boundary condition:
For x=0, T=T0, which gives us:
T_0-T_{\infty}=c_1+c_2
2nd boundary condition:
Here we assume that at the end of the fin (x=L), no more heat conduction is possible and with Fourier's law that means:
\Big(\frac{d\tau}{dx}\Big)_{x=L}=0
\implies \frac{d\tau}{dx}=mc_1e^{mx}-mc_2e^{-mx}
c_1e^{mL}-c_2e^{-mL}=0
Together with:
T_0-T_{\infty}=c_1+c_2
... it's a simple system of simultaneous equations, from which c1 and c2 can be computed (I won't do that here).
Inserting these constants into the proposed solution and very considerable rework then yields:
\frac{T-T_{\infty}}{T_0-T_{\infty}}=\frac{\cosh\Big(\big(1-\frac{x}{L}\big)\sqrt{\frac{hp}{kA}}L\Big)}{\cosh\Big(\sqrt{\frac{hp}{kA}}L\Big)}
Note that the hyperbolic cosine means:
\cosh f(x)=\frac{e^{f(x)}+e^{-f(x)}}{2}
Heat dissipated by the cooling fin:
More important than the temperature profile of the fin is how much heat it withdraws from the wall (that is after all its purpose).
Because we're in steady state, we can calculate this as the heat conducted into the fin at the interface with the wall. That heat is then also what is
dissipated by the fin because Qin=Qout. With Fourrier's law:
\dot{Q}_{x=0}=\left.-kA\frac{d}{dt}(T-T_{\infty})\right|_{x=0}
I'll only present the result here:
\dot{Q}_{x=0}=\sqrt{khpA} (T-T_{\infty})\tanh mL
With:
\tanh mL=\frac{e^{mL}-e^{-mL}}{e^{mL}+e^{-mL}}
An inspection of tanh ml shows that it increases with L but that there's hardly any more gain in Q for mL > 3. Excessively long
fins hardly dissipate more heat than reasonably shorter ones.
[Edited on 9-5-2016 by blogfast25]
|
|
|
Eosin Y
Banned troll
 
Posts: 83
Registered: 8-5-2016
Location: Eton College science department
Member Is Offline
Mood: Aga needs to cool his heels
|
|
@Blogfast25 are you a maths teacher? I'm in top maths set (out of 14) in the first year of British boarding school, and this goes right over my head.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Bloggers is all sorts of teacher, and pretty good at it too.
Just start with the first page of this thread.
I started there knowing just about nothing about calculus, apart from how to spell it.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Eosin Y  | | @Blogfast25 are you a maths teacher? I'm in top maths set (out of 14) in the first year of British boarding school, and this goes right over my head.
|
No, I'm a Uni degree engineer (chemistry) but I love math.
Have you done any calculus (in particular rates and derivatives) in that first year at all? I thought that was more sixth form (or a bit
before), vaguely remembering from my daughter's British education.
And second order ODEs aren't part of the A-level curriculum at all, IIRW...
[Edited on 9-5-2016 by blogfast25]
|
|
|
Eosin Y
Banned troll
 
Posts: 83
Registered: 8-5-2016
Location: Eton College science department
Member Is Offline
Mood: Aga needs to cool his heels
|
|
Sort of. We've gone over what it is (basics viz. that it is the study of the function relative to the change in input) but we haven't got any further
than that.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Experimental determination of heat conductivity k:
Finally another example of heat applied but this one without second order DEs!
The following set up allows the determination of the heat conductivity k on uniform, non-metallic materials:
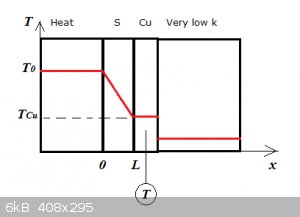
A slab of the sample S is sandwiched between a heat source at constant T0 and a thin slab of copper. The copper slab is held
against a highly insulating wall (very low k), so no heat can escape from the copper slab. The sample and copper slab thus heat up in time.
A thermocouple measures the temperature of the copper slab during the experiment.
The heat flux through the sample slab can be calculated using Fourier:
\dot{Q}=-kA\frac{dT}{dx}
-kA\int_{T_0}^{T_{Cu}}dT=\dot{Q}\int_0^Ldx
\dot{Q}L=-kA(T_{Cu}-T_0)
\dot{Q}=-\frac{kA}{L}(T_{Cu}-T_0)
For the copper slab, assuming it's fairly thin, we assume a quasi-steady state, where:
\frac{dT}{dx}=0
Because Cu is such an excellent heat conductor and because the Cu is thinish that's a reasonable assumption.
With no heat lost, the copper slab will now heat up acc.:
\dot{Q}=mc_p\frac{dT_{Cu}}{dt}
With m the mass of Cu and cp the specific heat capacity of Cu. So we have an identity:
mc_p\frac{dT_{Cu}}{dt}=-\frac{kA}{L}(T_{Cu}-T_0)
This simple first order DV with separation of variables solves as:
\frac{dT_{Cu}}{T_{Cu}-T_0}=-\frac{kA}{mc_pL}dt
\int_{T_{Cu,i}}^{T_{Cu,t}}\frac{dT_{Cu}}{T_{Cu}-T_0}=-\frac{kA}{mc_pL}\int_0^tdt
\ln \frac{T_{Cu,t}-T_0}{T_{Cu,i}-T_0}=-\frac{kA}{mc_pL}t
Where TCu,i is the initial (t = 0) temperature of the copper slab.
Measuring TCu,t over time and plotting the left hand expression versus time gives a straight line with slope:
-\frac{kA}{mc_pL}
... from which k can then be calculated.
One thing that's neat about the method is that it requires no knowledge of the specific heat capacity of the sample material.
[Edited on 10-5-2016 by blogfast25]
|
|
|
Eosin Y
Banned troll
 
Posts: 83
Registered: 8-5-2016
Location: Eton College science department
Member Is Offline
Mood: Aga needs to cool his heels
|
|
I think that this is calculus, in that it is an equation dedicated to the function relative to the input. Sorry if this is in the wrong thread. The
following equation is for calculation of the VoD of energetics.
D=A(X(squared by 1/2))*(1+BP) where A=1.01, B=1.30, X=N*(M(squared by 1/2))*(Q(squared by 1/2)) and P = initial density. N=number of moles of gaseous
detonation products, M=avg. mol weight of these products and Q=chemical energy of detonation reactivity. This was dug up from a piece of old
literature.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
D=AX^{\frac12}(1+BP)
X=NM^{\frac12}Q^{\frac12}
Something like that?
TBH I'm not really sure what you mean by "X(squared by 1/2)"?
|
|
|
Eosin Y
Banned troll
 
Posts: 83
Registered: 8-5-2016
Location: Eton College science department
Member Is Offline
Mood: Aga needs to cool his heels
|
|
Yes, exactly that. I couldn't think of a better way to explain it. How tf do you get those equations in your posts?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
SM supports LaTeX commands.
if you type two $ together, followed by this :
\int_{T_{Cu,i}}^{T_{Cu,t}}\frac{dT_{Cu}}{T_{Cu}-T_0}=-\frac{kA}{mc_pL}\int_0^tdt
and then another two $ together, you get this :
\int_{T_{Cu,i}}^{T_{Cu,t}}\frac{dT_{Cu}}{T_{Cu}-T_0}=-\frac{kA}{mc_pL}\int_0^tdt
If you hover over one of that (or any) formulae and right click, a menu pops up which lets you see the raw command syntax.
|
|
|
| Pages:
1
..
12
13
14
15
16
..
19 |