| Pages:
1
..
9
10
11
12
13
..
19 |
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Projectile velocity problem:
A 50 kg mass is shot from a cannon straight up with an initial velocity of 10m/s off a bridge that is 100 meters above the ground. If air resistance
(drag force Fd) is given by 5v determine the velocity of the mass when it hits the ground.
Solution: First, notice that when we say straight up, we really mean straight up, but in such a way that it will miss the bridge on the way back down.
Here is a sketch of the situation.
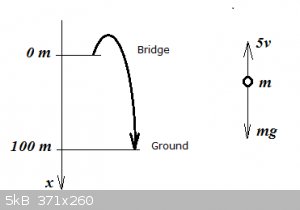
According to Newton’s Second Law, the projectile will experience acceleration acc.:
$$ma=mg-F_{drag}$$
$$a=\frac{dv}{dt}=v’$$
$$v'=g-\frac{F_{drag}}{m}$$
$$v’=9.8-\frac{5v}{50}=9.8-\frac{v}{10}$$
Initial condition:
$$t=0,v(0)=-10$$
This is a two-step problem. Firstly find an expression for v(t) from the above.
[Edited on 22-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. So will start at 10m/s going Up, reduce to 0 then accelerate Down at 9.81m/s/s from whatever height it was at at the 0 point, so we got to find
that initial height, add 100m and then work out it's velocity when it hits the floor, i.e. terminal velocity.
Sweet Jesus, help me !
[Edited on 22-4-2016 by aga]
Oh. You did by getting bloggers to add the initial equations. ah. thanks.
[Edited on 22-4-2016 by aga]
While we're at it, is bloggers the consumate Calculus devil or an angel on a deep-cover operation ?
[Edited on 22-4-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
While we're at it, is bloggers the consumate Calculus devil or an angel on a deep-cover operation ?
|
Not sure about me but there is such a thing called the Devil's curve...
[Edited on 22-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. So before i miss another C, here's the Plan :
Assuming that the cannon is on a retractable arm that removes the cannon immediately after firing (so we got true straight up/straight down motion),
we have to calculate distance travelled from the firing point to the 0m/s point at the top (of the arc in the sketch).
Add that to 100m then calculate the velocity of the mass when it hits the ground.
It will accelerate down from there by 9.8 m/s/s as per the question data, adjusted by the drag factor.
The 5v is giving me some concern, as in 'what units ?', although i suspect that is because i have not done the calculations yet.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | OK. So before i miss another C, here's the Plan :
Assuming that the cannon is on a retractable arm that removes the cannon immediately after firing (so we got true straight up/straight down motion),
we have to calculate distance travelled from the firing point to the 0m/s point at the top (of the arc in the sketch).
Add that to 100m then calculate the velocity of the mass when it hits the ground.
It will accelerate down from there by 9.8 m/s/s as per the question data, adjusted by the drag factor.
The 5v is giving me some concern, as in 'what units ?', although i suspect that is because i have not done the calculations yet.
|
Haha, like your removable cannon idea!
$$F_{drag}=5v$$
$$5\:\mathrm{Nm^{-1}s}$$
The only solution here is to calculate the total flight time, then use that as input into v(t) to find vground.
For that, develop an expression for v(t).
Then we'll develop an expression for x(t):
$$x(t)=\int v(t)dt$$
But FIRST, develop v(t). Presto!
[Edited on 23-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
A direction-changing two-dimensional parabola (time is one ..)
OK.
I'll have to invoke the Beer Ammendment and attempt it on the 'morrow.
Side-note:
Do you find these bits of maths Easy ?
Currently i find them really really hard (as you may have noticed).
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | A direction-changing two-dimensional parabola (time is one ..)
OK.
I'll have to invoke the Beer Ammendment and attempt it on the 'morrow.
Side-note:
Do you find these bits of maths Easy ?
Currently i find them really really hard (as you may have noticed). |
Strictly speaking we should do the whole thing in vector calculus:
$$\frac{d\vec{v}}{dt}=\vec{g}-5\vec{v}$$
Does that make it any clearer?  As luck has it, here we can deal with the
scalars (magnitude and sense of the vectors) only, as above.
Easy? Maybe not but it really is all about practice. I've been using calculus for over 30 years now. 
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
30 years !
Oh dear.
Can i at least write a letter to my mum before all the Whipping starts ?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Keep it short, boy.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
With approriate trepidation ...
$$a=v'=\frac {dv}{dt} = 9.8-\frac{v}{10} = \frac {98-v}{10}$$
$$\frac {dv}{dt} = \frac {98-v}{10}$$
$$dt = \frac {10dv}{98-v}$$
let u=98 - v
$$u' = du = (98-v)'dv = -dv$$
$$dv = -du$$
$$dt = -10 \frac {du}{u}$$
$$\int dt = -10 \int \frac {du}{u}$$
$$t = -10 ln(u)+C$$
$$C = t+10 ln(u) = t+10 ln(98-v)$$
bung in the starting conditions
$$\therefore C = 0+10 ln(98+10) = 46.82$$
now re-arrange
$$t = -10ln(98-v)+46.82$$
$$t-46.82 = -10ln(98-v)$$
$$\frac {46.82-t}{10} = ln(98-v)$$
$$e^{\frac {1}{10} (46.82-t)} = 98-v$$
$$v = 98 - e^{\frac {1}{10} (46.82-t)}$$
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
So sorry I missed this for some reason.
Your solution is:
{Drum roll}...
{another drum roll...}
{final, longer drum roll!}
100 % correct!
A slightly simpler form (but equal to yours) is:
$$v(t)=98-108e^{-0.1t}$$
<hr>
Next step: calculate total flight time. For this we need an expression for x(t):
$$v(t)=\frac{dx(t)}{dt}$$
$$\implies x(t)=\int v(t)dt$$
Initial condition:
$$t=0, x(0)=0$$
Chop, chop!
[Edited on 25-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Do what ?!?!
How the F is
$$98 - e^{\frac {1}{10} (46.82-t)} = 98-108e^{-0.1t}$$
I'm not an habitual 'e' user so don't look quite so surprised, Sir.
By the looks of things, i think i shall keep wearing the extra-thick cow-hide leather unterhosen.
|
|
|
j_sum1
Administrator
Posts: 6320
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
$$98 - e^{\frac {1}{10} (46.82-t)} = 98 - e^{(4.682-0.1t)}=98 - e^{4.682}e^{-0.1t}=98-108e^{-0.1t}$$
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
A fundamental property of exponentials:
$$e^{a-b}=e^ae^{-b}$$
Here a = 46.82/10 and b = -0.1.
$$e^{4.682}=108$$
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Well i'll be !
It's really getting annoying how many holes on my knowledge there actually are.
Guess i should have studied longer.
Edit:
Will your solution work out easier than mine in the next step ?
I'm guessing it will.
[Edited on 25-4-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
My shape of the solution is a bit easier to integrate, yes.
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Delay due to this little bugger is giving me a hard time :
$$e^-\frac{1}{10}t$$
Not given up, just need to learn about e and how to flip it about.
Still calculating.
[Edited on 26-4-2016 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Chain rule, g-dammit!
Looks like there might be some whipping today, kids... 
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
i keep trying u = - t/10 and it bites me a lot.
Perhaps u = e ^ -1/10t will like a biscuit.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
I spy with my little eye, something like this:
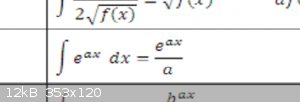
[Edited on 26-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
A Cheat Sheet - brilliant !
That e jobbie makes things much simpler.
$$x(t)=\int v(t)dt$$
$$x(t)=\int 98-108e^{-0.1t} dt$$
$$98\int dt - 108\int e^{-0.1t} dt$$
$$98t - \frac { 108e^{-0.1t}}{-0.1} + C$$
$$98t + 1080e^{-0.1t} + C$$
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
With x=t=0, i get C=-1080
Try as i might, i can't isolate 't'
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
$$C=-1080$$
... is correct!
So we get:
$$x(t)=98t+1080e^{-0.1t}-1080$$
And no, you can't isolate t from that. To find the flight time, we set x(t) = 100:
$$100=98t+1080e^{-0.1t}-1080$$
This is a transcendental equation that has no analytical solution. But it does have a numerical solution, which I give you:
$$t=5.98\:\mathrm{s}$$
Now plug that into v(t) to get final velocity.
PS. That 'cheat-sheet' has been posted here at least twice before!
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
25.51 m/s
I was thinking that the total distance travelled would be the Up part (approx 9m) plus the 100m drop.
Cheat sheet bookmarked, thanks.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | 25.51 m/s
I was thinking that the total distance travelled would be the Up part (approx 9m) plus the 100m drop.
Cheat sheet bookmarked, thanks. |
$$v=98-108e^{-0.1t}$$
$$t=5.98$$
$$v=98-108e^{-0.598}=38.6\:\mathrm{m/s}$$
'Total distance travelled': a common misconception. x(t) is simply the position of the object in the coordinate system I gave you (so
generously!). The total difference travelled could also be calculated by calculus but it doesn't help us here.
<hr>
We're nearing the end of our little journey into basic calculus.
In the following few sessions I'll briefly touch upon:
1. Partial derivatives.
2. Simple multi-variate optimisation problems.
2. A few important second order differential equations.
[Edited on 27-4-2016 by blogfast25]
|
|
|
| Pages:
1
..
9
10
11
12
13
..
19 |
![[*]](images/xpblue/default_icon.gif){kind=icon}
