Sciencemadness Discussion Board - Calculus! For beginners, with a ‘no theorems’ approach!


	Not logged in [Login ]

FAQ

Member List

Today's Posts Forum Stats

Stats

Back to:

Sciencemadness Discussion Board » Fundamentals » Miscellaneous » Calculus! For beginners, with a ‘no theorems’ approach!

Printable Version

Pages: 1 .. 8 9 10 11 12 .. 19

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 17-4-2016 at 08:27

Quote: Originally posted by blogfast25

Did you take into account the surface area of the top and bottom?

I'm curious to see your data and how you will derive your estimate of h from them. :cool:

I know how I would.

Erm, i added the area of the middle bit to the last bit but not the other bit, so it could be a way out.

It wasn't clear whether that formula for 'area of a cone' was the entire cone. I assumed it was.

Raw data:-

Secs deg C
0 62
60 60
120 57
180 56
240 55
300 54
360 53.5
420 52
480 50.5
540 49
600 48

I just set the equation up in a spreadsheet, used the calculated values (also the s.h.c. of water @ 4.186) and tried 'h' numbers until the result roughly agreed with the experimental result.

Quicker for me that way.

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 17-4-2016 at 08:53

Quote: Originally posted by aga

I just set the equation up in a spreadsheet, used the calculated values (also the s.h.c. of water @ 4.186) and tried 'h' numbers until the result roughly agreed with the experimental result.

Quicker for me that way.

The scientific way of doing this would be as follows.

Remember that:

$\ln \Big[\frac{T-T_a}{T_i-T_a}\Big]=-\tau t$

You would plot in Excell:

$\ln \Big[\frac{T-T_a}{T_i-T_a}\Big]$

versus:

$t$

That should give something looking like:

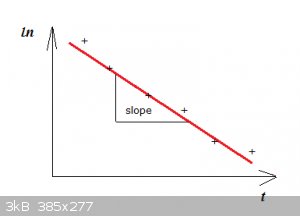
The + are the data points, they should roughly be on a straight line. Then make Excell fit a line to the data (linear regression).

The slope of the line is:

$-\tau$

Then calculate h from tau.

Acids and Bases: Brønsted–Lowry Theory (an interactive educational SM thread)

Quantum Mechanics/Wave Mechanics in Chemistry SM Thread

Solvation, solubility limits and solubility products: basic theory with worked examples (SM thread)

Calculus for beginners (SM thread): table of content

'Tie yourself to the mast my friend and the storm will end'

'This time next year Rodney, we'll be millionaires!'

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 17-4-2016 at 10:46

All day reviving algebra cells did not leave any brain capacity to learn what a linear regression was.

What does a second or third order integrally equation look like ?

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 17-4-2016 at 11:53

Checking surface area of the cup, by calculus.

For a revolution body:

Revolution body.png - 3kB

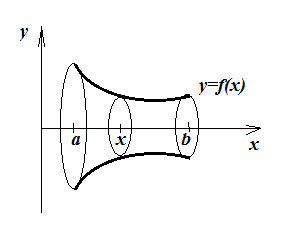
... the surface area A (end bits not counted) is given by:

$A=2\pi\int_a^bf(x)\sqrt{1+[f'(x)]^2}dx$
For the cup, with an x-axis running through it horizontal centre axis:

$f(x)=\frac{5}{17}x+70$

$f'(x)=\frac{5}{17}$

$A=2\pi\int_0^{85}\sqrt{1+\frac{5^2}{17^2}}(\frac{5}{17}x+70)dx$

$A=2.085\pi\Big[\frac{5}{34}x^2+70x\Big]_0^{85}=45927$
Lid:

$\frac{\pi}{4}95^2=7088$
Cone + lid:

$53015\:\mathrm{mm^2}=0.053\:\mathrm{m^2}$

Quote: Originally posted by aga

All day reviving algebra cells did not leave any brain capacity to learn what a linear regression was.

What does a second or third order integrally equation look like ?

If the first derivative is f'(x):

$f'(x)=\frac{df(x)}{dx}$

Then the second derivative is f''(x):

$f''(x)=\frac{df'(x)}{dx}=\frac{f^2(x)}{dx^2}$

$y'''=\frac{d(y'')}{dx}=\frac{d^3y}{dx^3}$

Example:

$m\frac{d^2y}{dt^2}=mg-ky$
or:

$my''=mg-ky$

Newtonian notation ('overdot notation'):

$m\ddot{y}=mg-ky$

... is the DE of motion of a bob of mass m hanging off a spring with spring constant k.

[Edited on 18-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 17-4-2016 at 12:50

Quote: Originally posted by blogfast25

$m\frac{d^2y}{dt^2}=mg-ky$

Is 'g' gravitational acceleration ?

Must be, seeing as it popped out of nowhere

You do realise that i'll soon be able to calculate proof for agaspace ...

Well, maybe if i can finally master those nasty fractions, do 'u' substitutions, drink less, think straight etc.

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 17-4-2016 at 13:39

Quote: Originally posted by aga

Quote: Originally posted by blogfast25

$m\frac{d^2y}{dt^2}=mg-ky$

Is 'g' gravitational acceleration ?

Yes. The bob is subject to it's own weight:

$mg$

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 17-4-2016 at 14:07

Of course, same as everything in agaspace, including Time : all attributes are inseparable.

$g' = \Sigma \int all o' t'otherbits$
Still regard these higher equations as 'best fit' or 'best we have found so far' mostly due to things like Limit Theorem : it's all basically an approximation, although a damned good one.

[Edited on 17-4-2016 by aga]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 17-4-2016 at 15:06

@aga:

I happen to know that for agaspace you need partial derivatives:

For a function f of x AND y:

$f(x,y)$
Partial derivative to x:

$\frac{\partial f}{\partial x}$
... and to y:

$\frac{\partial f}{\partial y}$

You can't calculate agaspace astral mass time differential tensors w/o them!

But we don't need them for agasyphon^TM, so we'll stick to the latter, tomorrow.

[Edited on 17-4-2016 by blogfast25]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 18-4-2016 at 04:58

Here's the plot for:

$\ln \Big[\frac{T-T_a}{T_i-T_a}\Big]=-\tau t$

$\Big[\frac{T-T_a}{T_i-T_a}\Big]$

... is also called the "Reduced Temperature", a dimensionless number between 1 and 0.

I used T_a=20 C.

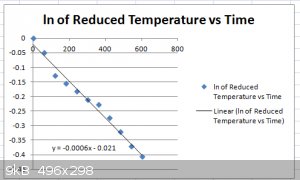
The linear regression equation:

$y=-0.0006x-0.021$

... gives us an estimate for:

$\tau=0.0006\:\mathrm{s^{-1}}$

$\tau=\frac{hA}{mc_p}$

With A=0.053 m², m=0.458 kg, c_p=4181 J/kg K then:

$h=\frac{\tau mc_p}{A}=22\:\mathrm{Wm^{-2}K^{-1}}$

Considering there's some noise on the data, this is a crude estimate, of course.

This source puts up a value range of 5 to 37 Wm^-2K^-1 for free convection in gas (air) or dry vapour, so we're in the right ball park.

[Edited on 18-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 18-4-2016 at 09:08

22 ?

Doh. I was very uncertain of the Units, so perhaps i got metres/millimetres mixed up somewhere.

$f(x,y,z)$
now that would definitely come in handy.

Quote:

astral mass time differential tensors

They sound very cool !

What colour are they ?

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 18-4-2016 at 09:14

Quote: Originally posted by aga

22 ?

Doh. I was very uncertain of the Units, so perhaps i got metres/millimetres mixed up somewhere.

$f(x,y,z)$
now that would definitely come in handy.

Quote:

astral mass time differential tensors

They sound very cool !

What colour are they ?

Perhaps the most common f(x,y,z) type function is the volume of a right angled box:

$V=lhw$

They're appleblueseagreen.

In a couple of hours: calculus of the agasyphon^TM. Yeehaw!

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 18-4-2016 at 10:45

Quote: Originally posted by blogfast25

Perhaps the most common f(x,y,z) type function is the volume of a right angled box:

$V=lhw$

Volume ! Of course !

So if the function f(x,y,z) is simply xyz, then f'(x,y,z) is one of the missing links with t ! (and E, maybe g as well)

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 18-4-2016 at 11:39

Syphon: tank emptying time

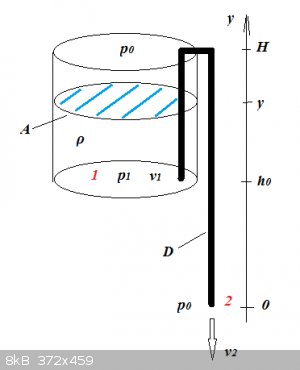
The tank's shape is of no consequence as long as its cross-section A is constant.

The outflow speed v₂ can be determined by applying Bernoulli's Principle between points 1 and 2:

$\frac12 v_2^2+gy_2+\frac{p_2}{\rho}=\frac12 v_1^2+gy_1+\frac{p_1}{\rho}$
The derivation is a bit lengthy, so I've posted it below the second page break.

The result is:

$v_2=c\sqrt{2gy}$
So the volumetric throughput Q_v is:

$Q_v=\frac{\pi}{4}D^2v_2=\frac{\pi}{4}D^2c\sqrt{2gy}$

During an infinitesimal amount of time dt, the water level decreases by dy (<0), so:

$dV=-Ady=Q_vdt$

$-Ady=\frac{\pi}{4}D^2c\sqrt{2hy}dt=\frac{\pi}{4}D^2c\sqrt{2g}\sqrt{y}dt$
Let's call:

$\alpha=\frac{\pi D^2c\sqrt{2g}}{4A}$

$-y^{-1/2}dy=\alpha dt$
Integrate between relevant boundaries:

$-\int_H^{h_0}y^{-1/2}dy=\int_0^t \alpha dt$

$2\big[\sqrt{y}\big]_{h_0}^H=\alpha t$

$t=\large{\frac{2}{\alpha}(\sqrt{H}-\sqrt{h_0})}$
Note that the higher up the tank is placed with respect to 0, the smaller t becomes.
<hr>
But. There's a big but.

The model above doesn't take into account any viscous losses in the syphon's pipe.

To take them into account, with Bernoulli, we get:

$\frac{1}{2c^2} v_2^2= gy-\frac{\Delta p_s}{\rho}$
For laminar flow (turbulent flow makes it more complicated) through the pipe:

$\Delta p_s=\frac{32 \mu L v_2}{D^2}$
Where:

$L \approx 2(H-h_0)+h_0$
Substituting we get:

$\frac{1}{2c^2} v_2^2= gy-\frac{32 \mu L v_2}{\rho D^2}$

$\frac12 v_2^2+\beta v_2-c^2gy=0$
With:

$\beta=\frac{32 \mu L c^2}{\rho D^2}$
This quadratic equation has one positive root:

$v_2=-\beta+\sqrt{\beta^2+2c^2gy}$
So:

$Q_v=\frac{\pi}{4}D^2v_2=\frac{\pi}{4}D^2(\sqrt{\beta^2+2c^2gy}-\beta)$
Inserting into the DV above the break:

$-\int_H^{h_0}\frac{dy}{\sqrt{\beta^2+2c^2gy}-\beta}=\int_0^t \alpha dt$
Where:

$\alpha=\frac{\pi D^2c}{4A}$
Although that integral is computable, the result gets very bulky and messy, so I won't go there.
<hr>
Full derivation:

$\frac12 v_2^2+gy_1+\frac{p_2}{\rho}=\frac12 v_1^2+gy_2+\frac{p_1}{\rho}$

$\frac12 (v_2^2-v_1^2)+\frac{p_0}{\rho}=gh_0+\frac{p_1}{\rho}$

$A_2v_2=Av_1$

$\implies v_2^2-v_1^2=v_2^2\Big[1-\Big(\frac{A_2}{A}\Big)^2\Big]$

$A_2=\frac{\pi}{4}D^2$

$\frac{1}{c^2}=[1-\Big(\frac{A_2}{A}\Big)^2\Big]$

$\frac{1}{2c^2}v_2^2+\frac{p_0}{\rho}=gh_0+\frac{p_1}{\rho}$

$p_1=\rho g(y-h_0)+p_0$

$\frac{1}{2c^2} v_2^2= gy$

$v_2=c\sqrt{2gy}$

$Q_v=\frac{\pi}{4}D^2v_2=\frac{\pi}{4}D^2c\sqrt{2gy}$

$dV=-Ady=Q_vdt$

$-Ady=\frac{\pi}{4}D^2c\sqrt{2hy}dt=\frac{\pi}{4}D^2c\sqrt{2g}\sqrt{y}dt$

$\alpha=\frac{\pi D^2c\sqrt{2g}}{4A}$

$-y^{-1/2}dy=\alpha dt$

$-\int_H^{h_0}y^{-1/2}dy=\int_0^t \alpha dt$

$2\big[\sqrt{y}\big]_{h_0}^H=\alpha t$

$t=\large{\frac{2}{\alpha}(\sqrt{H}-\sqrt{h_0})}$

But.

$\frac{1}{2c^2} v_2^2= gy-\frac{\Delta p_s}{\rho}$

$\Delta p_s=\frac{32 \mu L v_2}{D^2}$

$L \approx 2(H-h_0)+h_0$

$\frac{1}{2c^2} v_2^2= gy-\frac{32 \mu L v_2}{\rho D^2}$

$\frac12 v_2^2+\beta v_2-c^2gy=0$

$\beta=\frac{32 \mu L c^2}{\rho D^2}$

$v_2=-\beta+\sqrt{\beta^2+2c^2gy}$

$Q_v=\frac{\pi}{4}D^2v_2=\frac{\pi}{4}D^2(\sqrt{\beta^2+2c^2gy}-\beta)$

$-\int_H^{h_0}\frac{dy}{\sqrt{\beta^2+2c^2gy}-\beta}=\int_0^t \alpha dt$

$\alpha=\frac{\pi D^2c}{4A}$

[Edited on 19-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 19-4-2016 at 01:34

Cor Blimey !

I think a bit of commentary is going to be required to follow that properly !

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 19-4-2016 at 05:44

Quote: Originally posted by aga

Cor Blimey !

I think a bit of commentary is going to be required to follow that properly !

Ok. Briefly.

Often the preamble necessary to set up the DV is longer and harder work than actually solving the DV: that was definitely the case here.

The actual DV:

$dV=-Ady=Q_vdt$

... is obtained by looking at an emptying tank during an infinitesimally small t+dt time interval. In that time, a volume:

$Q_vdt$
Is discharged through the syphon. That causes the level in the tank to drop by -dy or a volume dV:

$dV=-Ady$

So:

$-Ady=Q_vdt$

Then it's a matter of plugging in Q_v, rearranging and integrating to get the tank's emptying time t.

Now look at:

$Q_v(y)=\frac{\pi}{4}D^2c\sqrt{2gy}$

This implies something anyone with a passing acquaintance of syphons will know: the lower you place the outlet (point 2), the higher the throughput!

This is also reflected by:

$t=\large{\frac{2}{\alpha}(\sqrt{H}-\sqrt{h_0})}$

Take values of H = 9 and h₀ = 4 (tank height is 5).

That gives:

$t=\frac{2}{\alpha}$

Now take values of H = 16 and h₀ = 11 (tank height is also 5).

That gives:

$t=\frac{1.37}{\alpha}$

32 % shorter!

Now for the case where we try and take pipe viscous losses into account:

$Q_v=\frac{\pi}{4}D^2(\sqrt{\beta^2+2c^2gy}-\beta)$

$\beta=\frac{32 \mu L c^2}{\rho D^2}$
If you look closely at that function, it appears that L on the one hand increases Q_v, on the other hand it seems to decrease it.

Could there be an optimum L?

We can find this by Optimum Theory, by evaluating:

$\frac{dQ_v}{dL}=0$

I did this and found no optimum. That's good news because it means that as in the simpler 'no pipe friction' case, the lower the syphon outlet is, the higher the output and the smaller the emptying time (there exists no optimum L beyond which that statement is no longer true).

The formula:

$t=\large{\frac{2}{\alpha}(\sqrt{H}-\sqrt{h_0})}$

... can be used for a lower limit estimate of the emptying time, bearing in mind that due to losses in the syphon the real emptying time will always be somewhat higher.
<hr>
Next up (20.00 h UTC): a CHEMICAL example, with 'student participation' (euphemism alert).

[Edited on 19-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 19-4-2016 at 08:09

Jeez. All that algebra is seriously heavy stuff.

Are all the students going to draw lots to decide who does the experiment(s) ?

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 19-4-2016 at 09:35

Quote: Originally posted by aga

Are all the students going to draw lots to decide who does the experiment(s) ?

Of course. But I've got some Darwins on a dead cert!

Re. the algebra, the next one is much lighter on it.

[Edited on 19-4-2016 by blogfast25]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 19-4-2016 at 12:18

Hydrogen generator: (student problem)

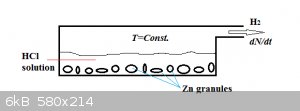
In the hydrogen gas generator above, a (constant) volume V of dilute hydrochloric acid of initial concentration c₀ reacts with zinc granules acc.:

Zn(s) + 2 HCl(aq) === > ZnCl₂(aq) + H₂(g)

We assume the amount of Zn (number of moles) present to be much, much higher than that of HCl and the temperature to be constant. In those circumstances kinetics allows us to write:

$\frac{dN}{dt}=kc$
N is the number of moles of hydrogen formed, t is time, k the reaction rate constant and c the hydrogen chloride concentration.

The concentration of HCl is obviously NOT constant, as each mol of hydrogen generated requires 2 mol of HCl to react away. Stoichiometrically we can write:

$c=\frac{c_0V-2N}{V}$

We start off at t=0 with N=0.

Develop expressions for:

1. N(t): the number of moles hydrogen generated as a function of time.

2. The rate of hydrogen generation dN(t)/dt as a function of time.

Heigh-ho, heigh-ho!
Off to work you go!

[Edited on 19-4-2016 by blogfast25]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 21-4-2016 at 13:27

Mini-recap on substitutions and differentiation

Suppose we have an integral of the type:

$\int \frac{dx}{ax+b}$
This can't be integrated directly because the stuff behind the d isn't the same as ax+b (differential doesn't match integrand).

To remedy this we try a substitution:

$u=ax+b$
Now derive:

$\frac{du}{dt}=a\frac{dx}{dt}+0=a\frac{dx}{dt}$
Multiply both sides by dt to obtain the differential:

$du=adx$

So:

$dx=\frac1a du$
Now substitute:

$\int \frac{\frac1a du}{u}$

$=\frac1a \int \frac{du}{u}$
Integrate this, then substitute back with u=ax+b.

Why this u-kerfuffle? Well, had we said that:

$\int \frac{dx}{ax+b}=\ln(ax+b)$ , that would have been incorrect because, if we take the first derivative, with the chain rule:

$[\ln(ax+x)]'=\frac{1}{ax+b}(ax+b)'=\frac{a}{ax+b}\neq \frac{1}{ax+n}$
But:

$[\frac1a \ln(ax+x)]'=\frac1a \times\frac{1}{ax+b}(ax+b)'=\frac1a \times \frac{a}{ax+b}$

$[\frac1a \ln(ax+x)]'=\frac{1}{ax+n}$
... which is correct.
<hr>
Here's a few more examples: remember that derivation and integration are anti-operators.

If:

$y=\int \cos 3xdx=\frac13 \sin3x+C$
Then:

$y'=[\frac13 \sin3x+C]'=\frac13 \times (\sin 3x)'+0$

$=\frac13 \times \cos 3x \times (3x)'=\frac13 \times \cos 3x \times 3=\cos 3x$
If:

$y=\int(5-x)^6dx=-\frac17(5-x)^7+C$
Then:

$y'=[-\frac17(5-x)^7+C]'=-\frac17 \times 7(5-x)^6 \times (5-x)'+0=-(5-x)^6 \times (-1)$

$=(5-x)^6$
If:

$y=\int e^{3-2x}dx=-\frac12 e^{3-2x}+C$
Then:

$y'=[-\frac12 e^{3-2x}+C]'=-\frac12 e^{3-2x} \times (3-2x)'+0$

$=-\frac12 e^{3-2x} \times (-2)$

$=e^{3-2x}$

[Edited on 22-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 22-4-2016 at 06:59

This sodding 'u' thing is doing my head in.

Let's see if i got it yet :

$\frac {dN}{dt}=kc$

$c=\frac {c_0V-2N}{V}$

$\frac {dN}{dt}=k \frac {c_0V-2N}{V}$

$\frac {dN}{c_0V-2N} = \frac kV dt$
let

$u = c_0V-2N$
Right. Here is where it gets messy.

$du = u' = (c_0V-2N)'$
Left-hand part first

$u' = 1du = du$
In the right-hand part only N is a variable, so we get the derivative of that, i.e. dN

$(c_0V-2N)' = (0-2)dN = -2dN$
overall, we get

$du = -2dN$
therefore

$dN = -\frac 12du$
so now we can substitute for dN in the next step and get all integrobblers the same species

$\frac {dN}{u} = \frac kV dt$
and finally integrate

$\int -\frac 12 du\frac 1u = \int \frac kV dt$

$-\frac 12 \int \frac {du}{u} = \frac kV \int dt$

$- \frac 12 ln(u) = \frac kV t$
substitute for u

$- \frac 12 ln(c_0V-2N) = \frac kV t$

$ln(c_0V-2N) = -2 \frac kV t$

$c_0V-2N = e ^{-\frac {2kt}{V}}$

$2N = c_0V - e ^{-\frac {2kt}{V}}$

$N = \frac 12 \Big( c_0V - e ^{-\frac {2kt}{V}}\Big)$

i'm assuming the C generated in each integration is the same C, so cancel out.

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 22-4-2016 at 07:13

I guess the rate of gas generation is the first derivative of that, which i think is

$-\frac 12 e^{-\frac {2k}{V}}$

[Edited on 22-4-2016 by aga]
Hang on, surely the Rate will depend on the concentration as well ?

Doh.

[Edited on 22-4-2016 by aga]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 22-4-2016 at 08:05

Quote: Originally posted by aga

i'm assuming the C generated in each integration is the same C, so cancel out.

Heck. Everything was 100 % correct up to that point.

$N = \frac 12 \Big( c_0V - e ^{-\frac {2kt}{V}}\Big)$

... is incorrect because:

$- \frac 12 \ln(c_0V-2N) = \frac kV t$

... should have been:

$- \frac 12 \ln(c_0V-2N) = \frac kV t+C$

$\implies \ln(c_0V-2N)=-2 \frac kV t -2C$

$c_0V-2N=e^{-2 \frac kV t -2C}=e^{-2C}e^{-2 \frac kV t}$
Now I'm gonna use a little trick that isn't indispensable but just helps a bit. e<sup>-2C</sup> is a constant too, so I'll call it K:

$c_0V-2N=Ke^{-2 \frac kV t}$
Now with the initial condition:

$t=0, N=0$

$c_0V=K$
So:

$N=\frac{c_0V}{2}\big(1-e^{-2 \frac kV t}\big)$
And:

$\frac{dN}{dt}=kc_0e^{-2 \frac kV t}$
We can see that these are correct because:

$t \to \infty \implies N=\frac{c_0V}{2}$

c₀V mol of HCl does indeed generate (c₀V)/2 mol of H₂.

Also:

$\Big(\frac{dN}{dt}\Big)_{t=0}=kc_0$
which is also correct.

That your solution was incorrect could be seen because you're subtracting a dimensionless number from moles. "apples minus oranges" error!

Quote: Originally posted by aga

I guess the rate of gas generation is the first derivative of that, which i think is

$-\frac 12 e^{-\frac {2k}{V}}$

[Edited on 22-4-2016 by aga]
Hang on, surely the Rate will depend on the concentration as well ?

Indeed, Sir. Indeed. QED.

[Edited on 22-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 22-4-2016 at 08:49

Oh bollocks.

Big fat fecking C bollocks !

Ah well, did i get into the top 30% for effort, or do i remain in the bottom 20% ?

[Edited on 22-4-2016 by aga]

blogfast25

International Hazard

Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline

Mood: No Mood

posted on 22-4-2016 at 10:07

Quote: Originally posted by aga

Oh bollocks.

Big fat fecking C bollocks !

Ah well, did i get into the top 30% for effort, or do i remain in the bottom 20% ?

[Edited on 22-4-2016 by aga]

Top 40 %!

One more problem coming up tonite, similar to this one (mathematically speaking). Hold beer till about 8 to 8.30 UTC.

After that: partial derivatives!

[Edited on 22-4-2016 by blogfast25]

aga

Forum Drunkard

Posts: 7030
Registered: 25-3-2014
Member Is Offline

posted on 22-4-2016 at 10:11

Quote: Originally posted by blogfast25

Hold beer till about 8 to 8.30 UTC.

Erm, er ...

Edit:

Adding that impossible task into the equation makes this possibly the most difficult SM page of all time !

[Edited on 22-4-2016 by aga]

Pages: 1 .. 8 9 10 11 12 .. 19

Sciencemadness Discussion Board » Fundamentals » Miscellaneous » Calculus! For beginners, with a ‘no theorems’ approach!