| Pages:
1
..
7
8
9
10
11
..
19 |
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by aga  | If expulsion does get discussed again, may i remind the teaching staff of the modulus of those negatives i still have in safe keeping from the 1992
school cultural visit to Paris.
You know, the ones of yourselves with 'Monsieur Fouetter la Derriere' at madame Fifi's place on the Rue de La Huchette ... |
I was only four years old in 1992! Shame on you!
P.S. - Blackmailer!
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Amazing. In 1992 i was almost exactly $$e^\pi$$
Yes, mail as black as blackest Coal.
Think of expulsion and i'll eat your soul !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Simple Differential Equations:
There exists an entire taxonomy of differential equations, classified by order (first order, second order), linear (or higher degree), homogeneous or
not and some special formats (Bernoulli, Clairaut, Legendre etc) but no overarching, uniform algorithm that would solve all of them.
It’s outside of the scope of this basic course to treat this whole characterisation and I’ll limit it to the most simple of first order DEs
(we’ll look at some simple and famous second order ones further ahead).
First Order Linear DEs:
The general format is:
$$y'+P(x)y=Q(x)$$
Where:
$$P(x),Q(x)$$
... are both smooth and continuous functions.
1. Either P(x) = 0 or Q(x) = 0 or P(x) = Q(x):
In all three cases the DE becomes separable:
$$P(x)=0$$
$$\implies y'=Q(x)$$
$$\implies \int dy=y=\int Q(x)dx$$
Or:
$$Q(x)=0$$
$$\implies y'+P(x)y=0$$
$$\implies y'=-P(x)y$$
$$\implies \frac{dy}{y}=-P(x)dx$$
$$\implies \int \frac{dy}{y}=-\int P(x)dx$$
$$\implies \ln |y|=-\int P(x)dx$$
Or:
$$P(x)=Q(x)$$
Example:
$$y'+y \sin x=\sin x$$
$$\implies y'=(1-y)\sin x$$
$$\implies \frac{dy}{1-y}=\sin x dx$$
$$\implies \int \frac{dy}{1-y}=\int \sin x dx$$
$$\implies -\ln |1-y|=-\cos x + C$$
2. Integrating factor:
In other cases we can attempt to solve the differential equation:
$$y'+P(x)y=Q(x)$$
... by means of an integration factor.
We define an integrating factor I:
$$I=e^{\int P(x)dx}$$
It can then be shown that:
$$y=\frac{\int I Q(x)dx+C}{I}$$
Example:
$$y'+\frac{3y}{x}=\frac{e^x}{x^3}$$
$$\int \frac{3}{x}dx=3\ln x=\ln x^3$$
$$\implies I=e^{\ln x^3}=x^3$$
$$\implies y=\frac{\int(x^3 \frac{e^x}{x^3})dx+C}{x^3}$$
$$\implies y= \frac{e^x+C}{x^3}$$
Note that using an integrating factor is mo silver bullet because if P(x) is ‘complicated’ then IQ(x)dx in not likely to
be analytically integratable.
Good results are often obtained when:
$$P(x)=-\frac{m}{x^n}$$
... where m and n are both positive integers.
<hr>
Exercise:
$$y'+\frac{2y}{x}=\frac{\sin x}{x^2}$$
[Edited on 14-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Yikes !
I think i have a note from my mum somewhere.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Perhaps Robo-Integrator suddenly regains some appeal? 
Next up: some real world examples...
[Edited on 14-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. All looks fine, right up to the integration factor example, apart from the logs.
Are these general Rules ? :
$$e^{\ln x^n}=x^n$$
$$n\ln x=\ln x^n$$
This step i do not follow at all:-
$$\int \frac{3}{x}dx=3\ln x$$
I was expecting it to be this infinte horror
$$\int \frac 3x dx = 3\int x^{-1}dx = \frac 30$$
Probably best to 'fess up now that that i do not know what logarithms are.
|
|
|
j_sum1
Administrator
       
Posts: 6333
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
Logarithms are fun!!! You are in for a treat.
And actually, you are probably very familiar with logarithms even if you don't know it. If you can multiply 1000×100,000 in your head by adding
three and five, then you are using logs.
The notation is a little bit of a dog when you first encounter it -- seems a bit unintuitive. But it has stuck because it is actually a really
practical notation whenever these things come up.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | OK. All looks fine, right up to the integration factor example, apart from the logs.
Are these general Rules ? :
$$e^{\ln x^n}=x^n$$
$$n\ln x=\ln x^n$$
This step i do not follow at all:-
$$\int \frac{3}{x}dx=3\ln x$$
I was expecting it to be this infinte horror
$$\int \frac 3x dx = 3\int x^{-1}dx = \frac 30$$
Probably best to 'fess up now that that i do not know what logarithms are. |
Re. the very last point, if the (natural) logarithm of y is x, so:
$$\ln y=x$$
Then:
$$y=e^x$$
Natural logarithms are the anti-functions of (e-based) exponential functions. Logs only have function values for y > 0 (because [ALWAYS!]
ex > 0).
Exception to the power rule of integration:
$$\int x^n dx=\frac{x^{n+1}}{n+1}+C$$
EXCEPT for:
$$n=-1$$
Then:
$$\int x^{-1}dx=\ln x+C$$
Otherwise we get the deadly 'division by zero error'!!!
<hr>
Some useful properties of logs:
$$\ln x^{n}=n \ln x$$
$$\ln (A . B)=\ln A+ \ln B$$
$$\ln \frac{A}{B}=\ln A -\ln B$$
The latter property is commonly used when a determined integral is of the shape:
$$\Delta y=\Big[\ln F(x)\Big]_a^b=\ln F(b)-\ln F(a)=\ln \frac{F(b)}{F(a)}$$
[Edited on 15-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by blogfast25  | Exception to the power rule of integration:
$$\int x^n dx=\frac{x^{n+1}}{n+1}+C$$
EXCEPT for:
$$n=-1$$
Then:
$$\int x^{-1}dx=\ln x+C$$ |
Aha ! Wasn't aware of the exception.
My calculator pukes for both formulae if x = 0, n = -1
Does the 'normal' rule hold true for all other -ve values of n ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The power rule hold for ALL values of n, including negative ones, EXCEPT for n = -1. Even for values very close to -1 it holds. But
NOT for n = -1.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Train stopping problem:
Although this problem can also be solved in a quicker way, using calculus is a nice, simple demonstration of calculus in kinematic problems, so here
goes...
A 150-car freight train is approaching Carbondale, Yorkshire at a constant speed of 15 meter per second (approximately 34 mph). As the train nears a
railroad crossing, the locomotive engineer sees a car stalled on the tracks. It takes him 4 seconds to react before he applies the brakes. It then
takes the train another 1.25 minutes to come to a full stop. Assume that the deceleration of the train is constant while the brakes are being applied.
How far does the train travel from the moment the engineer sees the car until the time the train comes to a full stop?
Schematic:
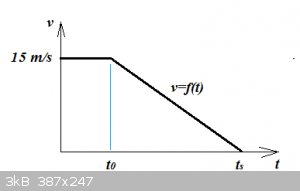
Let’s express the basic data in ‘mathspeak’:
$$v_0=15\;\mathrm{m/s}, t_0=4\:\mathrm{s}, t_s-t_0=1.25\:\mathrm{min}=75\:\mathrm{s}$$
We imagine the train to run along a x-axis, pointing in the direction of motion.
Now we take a quick short cut, to calculate the deceleration during the braking period.
$$a=\frac{\Delta v}{\Delta t}=\frac{0-v_0}{t_s-t_0}=-\frac{15}{75}=-\frac15=-0.2\:\mathrm{m/s^2}$$
So the train's velocity is reduced by 0.2 m/s, per second of braking.
The velocity – time function is not smooth and continuous because v suddenly changes at t=4 s. For that reason we’ll ignore what went on before
t=4 s, at least for now.
From higher up in the thread we know that:
$$a=\frac{dv}{dt}$$
$$dv=adt$$
$$\int dv=\int adt=a\int dt$$
$$v=-\frac15 t+C$$
Using the boundary condition:
$$t=4, v=15$$
$$\implies 15=-\frac15 \times 4+C$$
$$C=\frac{79}{5}$$
$$\implies v=-\frac15 t+\frac{79}{5}$$
So the v,t function (for t > 4 s) is:
$$v=\frac15(79-t)$$
We also know that
$$v=\frac{dx}{dt}$$
$$dx=vdt$$
To calculate the travelled distance during braking we can apply:
$$\Delta x=\int_4^{79} vdt=\int_4^{79} \frac15 (79-t)dt$$
$$=\frac15\big[79t-\frac12 t^2\big]_4^{79}=562.5\:\mathrm{m}$$
Now we need to add the distance travelled during the 4 seconds before the driver puts on the brakes:
$$4 \times 15=60\:\mathrm{m}$$
So the total distance travelled between the driver noticing the car and full stop is 622.5 m.
[Edited on 15-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Wow. I can actually read and follow that !
Some beer cells must still be firing, thanks to your teaching skills.
In the missing steps after this step :
$$\frac15\big[79t-\frac12 t^2\big]_4^{79}$$
does the 1/5 apply to both bits or to the overall result ?
Second thoughts, don't tell me. I'll try it and see, most likely tomorrow and most likely it does apply to both bits.
Edit:
Thinking about it, it doesn't matter either way, same result happens.
[Edited on 15-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
In the missing steps after this step :
$$\frac15\big[79t-\frac12 t^2\big]_4^{79}$$
does the 1/5 apply to both bits or to the overall result ?
|
Let's nip that bit of confusion in the bud immediately: 1/5 is a factor and applies to everything between the brackets. So calculate the bit
between [ ] brackets first, then multiply by the factor.
Learning to read calculus problems is a already a huge step forward (seriously!) 
[Edited on 15-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Damn. I just though i'd gotten all brainy, only to find you're more so.
The logic was that the deceleration period applies only to that one linear chunk, so the boundaries are from 0 to 75, not 4 to 75.
'a' is calculated slightly differently (-ve cos it's decelleration not acceleration)
$$\text a = deceleration = {initial speed/time} = 15/75 = -0.2 = - \frac 15$$
The rest follows just about the same as you did, with interim steps so i don't get (more) confused
$$\int dv = \int adt = a\int dt$$
$$v = - \frac 15 \int dt = -\frac 15 t + C = C - \frac 15 t$$
we know v=0 at time 75s, so
$$0 = C - \frac {75}{5}$$
$$C = 15$$
alternately at time 0, C = v = 15. So now
$$v =15 - \frac 15 t = \frac {75-t}{5} = \frac 15(75-t)$$
therefore from t=0 to t=75
$$\Delta x = \int _0^{75} vdt = \int _0^{75} \frac 15(75-t)dt$$
This is a different integration so another C should appear
$$x=\frac 15 \Big[ 75t - \frac {t^2}{2} +C_2\Big]_0^{75}$$
$$x = \frac 15 \Big( [ (75)75 - \frac {75^2}{2} + C_2 ] - [ (0)75 - \frac {0^2}{2} + C_2] \Big)$$
Happily the subtraction eliminates this new constant
$$=\frac 15 [5625 - 2812.5 + C_2 - C_2] = \frac {2812.5}{5}= 562.5$$
add in the 4 secs @ 15m/s
$$= 562.5 + 60 = 622.5m$$
... exactly the same answer !
In't maffs amazing ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
It's totally maff!
Your way is how most would do it, BTW. But I'm an old oddball! 
One minor comment: when calculating:
$$\Big[\int f(x)dx\Big]_a^b=\Big[F(x)\Big]_a^b=F(b)-F(a)$$
... you don't need to invoke C because we know it will drop out. But what you wrote was mathematically correct nonetheless.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Hot Coffee: no need to blow on it!
So you've just bought yourself a cup of hot, steaming coffee in a flimsy throw away cup with lid. Now the annoyingly inevitable starts: it cools down
fairly quickly. In this exercise we'll try and model that cooling.
A few definitions and assumptions:
The coffee of mass m contains heat energy (Enthalpy) Q (J). Coffee has a specific heat capacity cp (J/kg K).
Heat loss (cooling) is through convective loss to the surrounding air (radiative losses are considered small at < 100 C).
Temperature of the coffee is more or less uniform throughout the cup.
In those circumstances Newton's cooling law tells us that:
$$-\frac{dQ}{dt}\propto A(T-T_a)$$
... where dQ/dt is the rate of heat loss energy, A is the total surface area of the cup, T is the temperature of the coffee and
Ta the ambient temperature (which is presumed constant). The negative sign is needed because dQ < 0 (it's a LOSS).
We can turn this into an identity by means of a proportionality constant h:
$$ \frac{dQ}{dt}=-hA(T-T_a)$$
h (W/K m2) is known as the Heat Transfer Coefficient. It's specific to each heating/cooling problem (it's not a universal constant). (in a
different context, double glazing people often refer to it as the "K-factor").
Thermodynamics also tells that when an object of mass m with specific heat capacity cp changes in temperature it's heat content also
changes acc.:
$$\Delta Q=mc_p\Delta T$$
By limit taking we can convert this into a differential equation:
$$\lim_{\Delta T \to 0}\frac{\Delta Q}{\Delta T}=\frac{dQ}{dT}=mc_p$$
$$\implies dQ=mc_pdT$$
Inserting this into the second equation above we get:
$$mc_p\frac{dT}{dt}=-hA(T-T_a)$$
Or:
$$\frac{dT}{dt}=-\frac{hA}{mc_p}(T-T_a)$$
Now we call ('tau'):
$$\tau=\frac{hA}{mc_p}$$
$$\frac{dT}{dt}=-\tau (T-T_a)$$
$$\frac{dT}{T-T_a}=-\tau dt$$
Because:
$$d(T-T_a)=dT-0=dT$$
$$\implies \frac{d(T-T_a)}{T-T_a}=-\tau dt$$
We can now integrate both sides directly, using the boundary conditions:
$$(t=0, T=T_i),(t, T)$$
... where Ti is the initial temperature of the coffee and T the temperature after some time t, so:
$$\int_{T_i}^{T}\frac{d(T-T_a)}{T-T_a}=-\int_0^t\tau dt$$
Remembering the properties of logs (  ), we get: ), we get:
$$\big[\ln(T-T_a)\big]_{T_i}^{T}=-\tau t$$
$$\ln \Big[\frac{T-T_a}{T_i-T_a}\Big]=-\tau t$$
$$\frac{T-T_a}{T_i-T_a}=e^{-\tau t}$$
$$\large{T=T_a+(T_i-T_a)e^{-\tau t}}$$
The temperature thus evolves as follows (schematic):
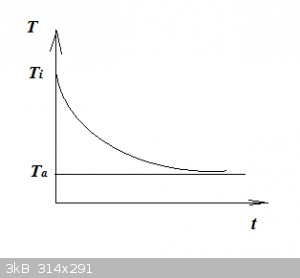
Evaluate (qualitatively):
1. The time needed to reach Ta.
2. The influence of h, A, m and cp on the cooling process.
[Edited on 16-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
You might know that, but for me, only having seen C a matter of minutes ago, i felt it important to remember that it does appear then
drop out.
That working-out/post is also intended to be useful for me to refer back to.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
You might know that, but for me, only having seen C a matter of minutes ago, i felt it important to remember that it does appear then
drop out.
That working-out/post is also intended to be useful for me to refer back to. |
I am a maff-nerd and I endorse those messages! 
[Edited on 16-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by blogfast25  | Evaluate (qualitatively):
1. The time needed to reach Ta.
2. The influence of h, A, m and cp on the cooling process.
|
Erm, the 'qualitatively' part knocked me sideways
(my fall being broken by a rather large pile of empty beer cans, so no lasting damage)
What does the question mean ?
Come up with an equation that :-
1. predicts the time needed to reach Ta starting from an abitrary time T ?
2. re-arrange said equation into other equations so h, A, m and cp respectively are on the other side ?
Edit:
You ain't fooling nobody : tau is u in disguise, trying to sneak in via the back door.
[Edited on 16-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Erm, the 'qualitatively' part knocked me sideways
(my fall being broken by a rather large pile of empty beer cans, so no lasting damage)
What does the question mean ?
Come up with an equation that :-
1. predicts the time needed to reach Ta starting from an abitrary time T ?
2. re-arrange said equation into other equations so h, A, m and cp respectively are on the other side ?
Edit:
You ain't fooling nobody : tau is u in disguise, trying to sneak in via the back door.
|
Qualitatively means: without actual numbers or calculation.
How long for the coffee to completely cool to Ta?
How do m, cp, A and h affects cooling rate? Increase? Decrease? No influence?
I knew I should have chosen kappa instead of tau!
Tomorrow: aga's syphon!
[Edited on 16-4-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Great !
So for the coffee to cool to Ta it will take a little while.
For larger cups, it will take little bit longer.
As-per definition perhaps, although i suspect that's not the answer required.
Heigh-ho. More algebra in the morning.
Oh. aga's syphon can be observed, measurements taken, even calculated, but absolutely no touching or photographs.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Recording the temperature of the first coffee of the day over 600 secs came up with some data that enabled a heat transfer coefficient (h) of 0.0463
for this system (i.e. this particular cup of coffee) to be guestimated with a spreadsheet and a bit of successive approximation..
Most cups are basically a cone with the top chopped off, then inverted.
The volume of the cup is equal to the volume of the full cone less that of the smaller chopped off cone, same goes for the area, although the area of
the bottom must be added.
Cone volume/area are given by
$$V=\pi r^2 \frac h3$$
$$A = \pi r (r +\sqrt{h^2 r^2})$$
Let (in millimetres)
ht = cup height
dt = diameter of the top of the cup
db = diameter of the bottom of the cup
Compute the volume and area of the cup (these bits took hours !) :-
$$mm^3 = \pi h_t \frac {d_t^3 - d_b^3}{12d_t-12d_b}$$
$$mm^2 = \pi \frac{d_t}{2} \Bigg( \frac {d_t}{2} + \sqrt { \Big(\frac {h_t d_t}{d_t-d_b} \Big)^2 + \frac {d_t^2}{4} } \Bigg) - \pi \frac{d_b}{2}
\Bigg ( \frac {d_b}{2} + \sqrt { \Big(\frac {h_t d_b}{d_t-d_b} \Big)^2 + \frac {d_b^2}{4} } \Bigg) + \pi \frac {d_b^2}{4}$$
THIS cup has the measurements :-
ht = 85mm
dt = 95mm
db = 70mm
So, it has a volume of 457,854 mm<sup>3</sup> = 458 ml and an area of 29,355mm<sup>2</sup> = 0.0294m<sup>2</sup>
It also went cold quote some time ago.
I'll get a beer instead and then have a go at the actual questions.
[Edited on 17-4-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by blogfast25  |
Evaluate (qualitatively):
1. The time needed to reach Ta.
2. The influence of h, A, m and cp on the cooling process. |
1.Mathematically the coffee will never reach ambient temperature (i.e. inifinite time).
In practice it reaches room temperature shortly before you finish doing whatever distracted you from drinking it hot (see above !)
2. less mass (m) = quicker coooling
less specific heat capacity (cp) = quicker cooling
less area (A) = slower cooling
less heat transfer coefficient (h) = slower cooling
[Edited on 17-4-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Well, well.
Decided to inject some experimentalism into it? Good!
I agree with your value of V but for A I get 0.0568 m2. I need to check that value, though. Did you take into account the surface area of
the top and bottom?
I'm curious to see your data and how you will derive your estimate of h from them.  I know how I would. I know how I would.
[Edited on 17-4-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Quote: Originally posted by blogfast25  |
Evaluate (qualitatively):
1. The time needed to reach Ta.
2. The influence of h, A, m and cp on the cooling process. |
1.Mathematically the coffee will never reach ambient temperature (i.e. inifinite time).
In practice it reaches room temperature shortly before you finish doing whatever distracted you from drinking it hot (see above !)
2. less mass (m) = quicker coooling
less specific heat capacity (cp) = quicker cooling
less area (A) = slower cooling
less heat transfer coefficient (h) = slower cooling
[Edited on 17-4-2016 by aga] |
All present and correct. 100/100. 
|
|
|
| Pages:
1
..
7
8
9
10
11
..
19 |