| Pages:
1
2
3
4
5
6
..
19 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@aga:
Apart from a few silly mistakes they're all good!
Wrong:
$$v'=2\Big(a+\frac1x)\Big.-x^{-2}$$
I think you just forgot to put in the multiplication sign. It should have been:
$$v'=2\Big(a+\frac1x\Big).-x^{-2}$$
Simplified:
$$v'=-\frac{2}{\sqrt{x}}\Big(a+\frac1x\Big)$$
Wrong but it was a hard one:
$$z'=e^{\sqrt{2-x^3}}.\frac12(2-x^3)^{-\frac12}$$
You still need to derive:
$$(2-x^3)'=-3x^2$$
and tag it onto your result, so it becomes:
$$z'=e^{\sqrt{2-x^3}}.\frac12(2-x^3)^{-\frac12}.(-3x^2)$$
Cleaned up:
$$z'=-\frac{3x^2}{2\sqrt{2-x^3}}e^{\sqrt{2-x^3}}$$
Wrong and very silly mistake:
$$f'=e^{0.5231x}.0$$
0.5231 is just a constant, so the derivative should have been:
$$f'=0.5231e^{0.5231x}$$
All in all fantastic progress, also on the LaTex!      
Last smallish batch of mixed exercises tomorrow, before normal service is resumed.
Stay tuned!
[Edited on 23-3-2016 by blogfast25]
|
|
|
Polverone
Now celebrating 21 years of madness
|
Thread Split
22-3-2016 at 17:09 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Not too bad for a beginner i guess.
This shakes the foundations a bit :
$$(2-x^3)'=-3x^2$$
Doesn't it go like this ? :
$$(2-x^3)'=2(-x^3)'$$
$$=2(-3x^2)$$
$$=-6x^2$$
I cannot quite see how you've cleaned up that square-rooty one.
Will try it myself later.
|
|
|
j_sum1
Administrator
       
Posts: 6250
Registered: 4-10-2014
Location: Unmoved
Member Is Offline
Mood: Organised
|
|
Nope. The 2 is just a constant.
On phone so won't attempt latex.
It ptobably looks more familiar written:
y= -x^3 + 2
y' = -3x^2
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The last five. They're not particularly difficult but I have 'mixed things up a bit':
$$y=\frac{4\cos x}{\sin 2x}+3x$$
$$u=x^3e^{2-x}$$
$$v=(x^2+x+1)e^x+\frac{1}{x-1}$$
$$z=[\ln(x-2)]^3$$
$$f=x^2\sqrt [3] {x^3-1}$$
Remember: loose talk costs lives, keep calm and carry on and a faulty derivative will set a missile on its creator rather than take to the
skies! 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
$$y=\frac{4\cos x}{\sin 2x}+3x$$
It looks like the sum rule and the quotient rule apply, so i'll venture :
$$y'=\Big(\frac{4cosx}{sin2x}\Big)'+(3x)'$$
$$y'=\frac{(4cosx)'(sin2x)-(4cosx)(sin2x)'}{(sin2x)^2}+(3x)'$$
$$y'=\frac{(-4sinx)(sin2x)-(4cosx)(cos2x)}{(sin2x)^2}+3$$
[Edited on 23-3-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Ah yes. Stupid mistake. I mistook it for a co-efficient somehow.
Cheers j_sum1.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
$$u=x^3e^{2-x}$$
Product rule ?
$$u=(x^3)(e^{2-x})$$
$$u'=(x^3)'(e^{2-x})+(x^3)(e^{2-x})'$$
... and the 'e' thing ...
$$u'=3x^2e^{2-x}+x^3e^{2-x}$$
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Minor error in y’, because:
$$(\sin 2x)’=2 \cos 2x$$
If in doubt:
Set:
$$u=2x$$
$$(\sin u)’= \cos u \times u’=\cos 2x (2x)’= 2 \cos 2x$$
Same type of mistake here:
$$u'=(x^3)'(e^{2-x})+(x^3)(e^{2-x})'$$
$$u'=3x^2e^{2-x}+x^3e^{2-x}(2-x)’$$
$$u'=3x^2e^{2-x}+x^3e^{2-x}(-1)$$
$$u'=3x^2e^{2-x}-x^3e^{2-x}$$
Further simplified:
$$u'=x^2 (3-x) e^{2-x}$$
[Edited on 23-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
$$v=(x^2+x+1)e^x+\frac{1}{x-1}$$
erm, er ... addition rule
$$v=[(x^2+x+1)e^x]+[\frac{1}{x-1}]$$
product rule
$$(x^2+x+1)e^x$$
quotient rule
$$\frac{1}{x-1}$$
if so ... it seems that parallel processing is required for each side, so left term first, rmembering the e on ya melon man:
$$(x^2+x+1)'(e^x)+(x^2+x+1)(e^x)'$$
$$=(2x+1)e^x+(x^2+x+1)e^x$$
simplify
$$v'=e^x(x^2+3x+2)$$
right side
$$\frac{(x+1)-(x+1)'}{(x+1)^2}$$
$$=\frac{x}{(x+1)^2}$$
result (hopefully) being :
$$=e^x(x^2+3x+2)+\frac{x}{(x+1)^2}$$
[Edited on 23-3-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Christ ! so the tiniest cock-up leads to enormously different results.
woelen is right : 100% meticulous or do not bother when it comes to these calculations.
Now might be a good time to ask what they are used for, as in what they apply to in the real world.
Edit:
Considering the difficulty of of Latex encoding, plus the first 'proper' view of the post after editing/previewing/posting, it might be a good idea
if the word 'final' was placed at the bottom of the post to signify that no further edits are to be made.
On another note, how come a 49 year old drunkard is the only person attempting these questions (and the latex encoding) ?
Where are all the seriously Smart young bucks ?
Probably jerking off in World of Warcraft etc.
Sad it's just me, again.
It's also a telling judgement on the character of the yobbo, Cou, LG2, quantumwhatever type trolls that they simply cannot focus their attention on a
subject for more than 5 seconds in order to learn something new.
If they Could, they'd get the near 1:1 attention i appear to get here, and from a Great teacher !
(Hmm. Maybe 2:1 cos i want to learn stuff too)
[Edited on 23-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
$$v'=e^x(x^2+3x+2)+\frac{x}{(x+1)^2}$$
... is spot on. Shows how being meticulous pays off. Do things in bite-size chunks.
Quote: Originally posted by aga  | Christ ! so the tiniest cock-up leads to enormously different results.
woelen is right : 100% meticulous or do not bother when it comes to these calculations.
Now might be a good time to ask what they are used for, as in what they apply to in the real world.
|
As regards applications, the first ones are coming up after these final exercises have been nailed.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Tantalatiousness !
I imagined a Spiral, where the change from one bit at the outside didn't change much between two points, then as you travel closer to the centre, the
change increases, and Probably the rate-of-change increases.
Beyond that, pretty clueless how these Fab maths tricks can be, applied, never mind actually used.
Hang on. If i were on a spiral train ride, and the car i was in were accellerating down the track, than i got a rate-of-change-of-a-rate-of-change or
something like that.
So deltaV=vomit ?
[Edited on 23-3-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Bugger. 2 more to do, and they look harder.
Late here so tomorrow sirrah'
N.B. not the first derivative of (sirrah) but a shakespearean device.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Maybe but what about :
$$z'$$
and
$$f'$$
?? 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
1 and 1.
Bed time. Oooh ! That sounds pervy !
The derivative of that statement is that i'm off to bed to give my liver some downtime.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. z' and f' :
$$z=[\ln(x-2)]^3$$
power and chain rules ?
$$z'=3[ln(x-2)']^2$$
$$z'=3\Big(\frac1{x-2}\Big)^2$$
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
$$f=x^2\sqrt [3] {x^3-1}$$
$$f=x^2(x^3-1)^\frac13$$
Power rule & Product rule
$$f'=(x^2)'(x^3-1)^\frac13+(x^2)[(x^3-1)^\frac13]'$$
$$f'=2x(x^3-1)^\frac13+x^2\frac13(x^3-1)^{-2/3}$$
$$f'=2x\sqrt[3]{x^3-1}+\frac{x^2}{3}\frac{1}{(x^3-1)^{2/3}}$$
Crap. I thought the -1/7 looked wrong.
1 sec please - learning about fractional powers where the dividend isn't 1...
[Edited on 24-3-2016 by aga]
[Edited on 24-3-2016 by aga]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
ok.
$$f'=2x\sqrt[3]{x^3-1}+\frac{x^2}{3}\frac{1}{(x^3-1)^{\frac23}}$$
$$f'=2x\sqrt[3]{x^3-1}+\frac{x^2}{3}\frac{1}{((x^3-1)^{\frac13})^2}$$
$$f'=2x\sqrt[3]{x^3-1}+\frac{x^2}{3}\frac{1}{(\sqrt[3]{x^3-1})^2}$$
$$f'=2x\sqrt[3]{x^3-1}+\frac{x^2}{3(\sqrt[3]{x^3-1})^2}$$
final.
The LaTeX command syntax is getting almost as intense as the maths ...
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Not really:
$$z'=3[\ln(x-2)']^2$$
Should be:
$$z'=3[\ln(x-2)]^2 \times [\ln(x-2)]'$$
$$z'=3[\ln (x-2)]^2 \frac{1}{x-2}(x-2)'$$
$$z'=3[\ln (x-2)]^2 \frac{1}{x-2}$$
Also:
$$f'=(x^2)'(x^3-1)^\frac13+(x^2)[(x^3-1)^\frac13]'$$
is correct but should become:
$$f'=2x(x^3-1)^\frac13+x^2\frac13(x^3-1)^{-2/3}(x^3-1)'$$
Etc...
Now have a look this, before we resume 'normal service':
<hr>
A little supplement for aga, about rate of change...
Imagine an object (symbolised by the star), moving along a horizontal x axis:
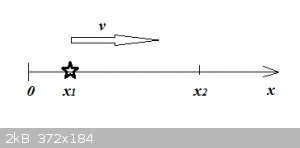
We don’t know at what speed the object moves or whether that speed is constant or not. Now assume the object changes position from
x<sub>1</sub> to x<sub>2</sub>, between time t<sub>1</sub> and t<sub>2</sub>. Then with:
$$\Delta x=x_2-x_1$$
and:
$$\Delta t=t_2-t_1$$
The average speed between these points would be:
$$v_{average}=\frac{\Delta x}{\Delta t}$$
But v<sub>average</sub> tells us almost nothing about how the speed differs from one instant to another.
To find the instantaneous speed in every instant t we need to calculate:
$$v(t)=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}=\frac{dx}{dt}$$
v(t) is the rate of position (x) change in time (syn.: as a function of time). If:
$$\frac{\Delta x}{\Delta t}=C$$
... with C a constant, then obviously the speed is constant: the rate of position change in time is then:
$$v(t)=C\:\mathrm{m/s}$$
But if:
$$v(t) \neq C$$
Then v(t) will be some function of time.
In that case we can define another rate of change: the rate at which v changes in time and it's called the
acceleration a. It can be defined analogously to the above reasoning as:
$$a=\frac{dv(t)}{dt}$$
In the (frequent) case where the acceleration is constant, say:
$$a=\frac{dv}{dt}=3\:\mathrm{m/s^2}$$
... then speed will increase by 3 m/s every second. The rate of change of speed then is 3 m/s<sup>2</sup> or 3 m/s per
second.
Of course an object may also be decelerating, in that case:
$$a=\frac{dv}{dt}<0$$
<hr>
Exercise:
If:
$$x(t)=3t^2+2t+4$$
Then what is:
$$v(t)$$
and:
$$a(t)$$
[Edited on 25-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Sorry, still fumbling about in the earlier errors, trying to see where i went disastrously wrong.
Very confused about what Rule applies where, and to which bits.
This is all new, so no experience to draw on.
I do wish somebody else would wish to learn this stuff.
It would be helpful to see how others approach a problem like these and how they'd solve it.
I guess all the nacent genii are all afraid that they'd come second to a drunkard. sigh. unlikely !
[Edited on 25-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Sorry, still fumbling about in the earlier errors, trying to see where i went disastrously wrong.
Very confused about what Rule applies where, and to which bits.
This is all new, so no experience to draw on.
I do wish somebody else would wish to learn this stuff.
It would be helpful to see how others approach a problem like these and how they'd solve it.
I guess all the nacent genii are all afraid that they'd come second to a drunkard. sigh. unlikely !
|
No, can't disagree with any of that.
Let me try again:
$$z=[\ln(x-2)]^3$$
Let's call:
$$p=\ln(x-2)$$
So:
$$z=p^3$$
$$z'=3p^2 \times p'$$
To find p', we have to apply the chain rule again:
$$p'=\frac{1}{x-2} \times (x-2)'=\frac{1}{x-2} \times 1=\frac{1}{x-2}$$
$$z'=3[\ln(x-2)]^2\frac{1}{x-2}$$
Another example:
$$f=[\sin (x^2)]^4$$
$$f'=4[\sin (x^2)]^3 \times [\sin (x^2)]'$$
$$[\sin (x^2)]'=\cos (x^2) \times (x^2)'=2x\cos (x^2)$$
So:
$$f'=8x[\sin (x^2)]^3\cos (x^2)$$
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Optimisation problems:
In this post it was shown that the derivative y’ of a function y can become zero for specific values of x, known as optima:
$$\Big(\frac{dy}{dx}\Big)_{x_{opt}}=y'(x_{opt})=0$$
This opens up the possibility of solving a whole range of optimisation problems: business owners want to maximise their profit function, rocket
scientists look for the longest possible range of their missiles, industrial chemists want to maximise yield of their processes, car makers try to
minimise fuel consumption of their creations, etc etc.
Most real world optimisation problems are multi-variable problems and mathematically outside the scope of this thread but below we’ll look at a few
simple single variable problems.
1. Simple function:
$$y=(x-2)^2+5$$
To find the optimum:
$$y'=2(x-2)(x-2)'+0$$
$$y'=2(x-2)(1)=2(x-2)$$
Optimum:
$$y'=2(x-2)=0 \implies x=2$$
And:
$$y=5$$
This is in fact a minimum of the function y.
2. Window size optimisation problem:
A window of the following shape needs to be constructed:
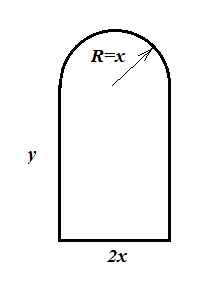
The window maker has only 12 m of frame material to work with. What are the dimensions x and y so that the window has maximum surface area S?
The circumference of the window is:
$$L=2x+2y+\pi x=12$$
The surface area is given by:
$$S=2xy+\frac{\pi}{2} x^2$$
Extract y from the first equation:
$$y=6-x-\frac{\pi}{2}x$$
And insert it into the second one:
$$S=2x(6-x-\frac{\pi}{2}x)+\frac{\pi}{2}x^2$$
$$S=12x-2x^2-\pi x^2+\frac{\pi}{2}x^2$$
If we assume this function has an optimum, then:
$$\frac{dS}{dx}=12-4x-2\pi x+\pi x=0$$
$$x=\frac{12}{4+\pi}=1.68\:\mathrm{m}$$
$$y=1.68\:\mathrm{m}$$
3. Can optimisation problem:
A manufacturer wants to produce a 1500 cm<sup>3</sup> capacity can, using as little material as possible:
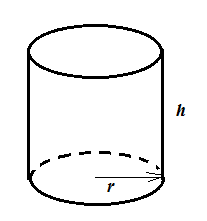
Total surface area of the can:
$$A=2\pi r^2+2 \pi rh$$
Total volume of the can:
$$V=\pi r^2h=1500\:\mathrm{cm^3}$$
Extract h from the second equation:
$$h=\frac{1500}{\pi r^2}$$
And insert it into the second one:
$$A=2\pi r^2+2 \pi r \frac{1500}{\pi r^2}=2\pi r^2+\frac{3000}{r}$$
To see if there’s an optimum, derive A to r:
$$\frac{dA}{dr}=4\pi r+\frac{0.r-3000}{r^2}=4\pi r-\frac{3000}{r^2}$$
Set the derivative to zero:
$$\frac{dA}{dr}=\frac{4\pi r^3-3000}{r^2}=0$$
We know that (always): $$r>0$$
So: $$4\pi r^3-3000=0$$
$$r=\sqrt[3]{\frac{3000}{4\pi}}=6.20\:\mathrm{cm}$$
$$h=12.4\:\mathrm{cm}$$
<hr>
Exercise:
It can be shown that the heat loss q (in Watt per unit of length) of a homogeneously insulated cylinder is given by:
$$q=\frac{\pi \Delta T}{\frac{1}{2k}\ln \frac{D}{d}+\frac{1}{hD}}$$
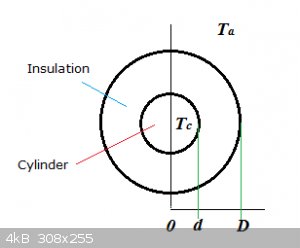
(Source)
Where T<sub>c</sub> is cylinder temperature, T<sub>a</sub> is ambient temperature, 2D is total diameter (insulation included),
2d is cylinder diameter. Note that:
$$\Delta T=T_c-T_a=\text{constant}$$
$$k\:\text{and}\:h\:\text{are both constants}$$
$$d=\text constant$$
Determine for which value of D, in function of k and h, q is minimised.
Hint:
Set:
$$q=\frac{\pi \Delta T}{u}$$
Then see if:
$$\frac{1}{u}$$
... has an optimum.
[Edited on 26-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Gah !
So obvious once you showed it !
It's hard to think outside the bin-bag.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
It's about seeing the 'structure' of the function: sums/subtractions, quotients and functions that are functions of other functions (chain rule).
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by blogfast25  | To find the instantaneous speed in every instant t we need to calculate:
$$v(t)=\lim_{\Delta t \to 0} \frac{\Delta x}{\Delta t}=\frac{dx}{dt}$$
v(t) is the rate of position (x) change in time (syn.: as a function of time). |
The "lim delta t->0" part is a mystery.
Basically i do not know how it is applied to the delta x/delta v part, so cannot compute the whole thing.
Sorry if my Density appears to be increasing.
|
|
|
| Pages:
1
2
3
4
5
6
..
19 |