| Pages:
1
2
3
4
5
..
33 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Particle in a one dimensional box
Although mainly a thought experiment (there exist some physical systems that resemble it, though) it’s an interesting one because despite its
simplicity it shows properties shared by nearly all other (bound particles) Quantum Systems. We’ll use the system here as an example to show
solutions of the Schrodinger equation and the properties of these solutions.
To make the system slightly more concrete, imagine the particle in a one dimensional box to be an electron, proton or other sub-atomic particle,
trapped in a straight micro-capillary tube which has been sealed shut at both ends. The particle is wholly confined to the tube. In physical terms
this means it would take an infinite amount of energy to ‘break out’ of this box.
Succinctly put, for a box from x = 0 to x = L ((“x between 0 and L”, box length L) the potential energy U(x) = 0 and for x < 0, U(x) = ∞ and
for x > L, U(x) = ∞. The latter two conditions are also known as an ‘Infinite Potential Energy Well’. Movement of the particle is therefore
restricted to the x- axis and between x = 0 and x = L.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pbox.html...
(Don’t follow any links on the above page yet)
Because of the U(x) = 0 for 0 <= x <= L (“x between 0 and L”) condition, the time independent one dimensional Schrodinger equation:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/scheq.htm...
… is simplified enormously: simply eliminate the U(x)ψ(x) term because U(x) = 0.
The solution of this ‘reduced’ equation is A-level math but I won’t provide the derivation here, only the solution:
Ψ<sub>n</sub>(x) = √(2/L) sin(nπx/L) (for x = 0 to x = L)
Pause. Stop the presses for a minute and let’s unpack this a bit.
Firstly, this isn’t just one wave function, it’s a whole bundle of them! An (theoretically) infinite bundle, to be precise:
Ψ<sub>1</sub>(x) = √(2/L) sin(πx/L), Ψ<sub>2</sub>(x) = √(2/L) sin(2πx/L), etc.
Because each value of n (allowed values are 1, 2, 3, 4…, ∞, positive integers in other words! Zero is NOT allowed) defines a specific
Ψ<sub>n</sub>(x).
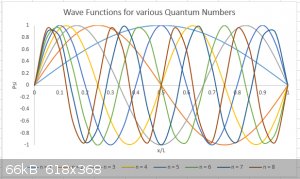
I’ve plotted below the first 8 (n = 1 to 8) wave functions for the particle in a one dimensional box, schematically (y axis is not to scale).
The number n is known as the Quantum Number of the system. Hurray! We’ve found the first Quantum Number in our course. Others will follow.
From this thought experiment can already be concluded a few really important things:
1. The Schrodinger Equation (SE) for bound particles yields a set of wave functions Ψ<sub>n</sub>(x).
2. The SE yields a Quantum Number n, each allowable value associated with one wave function. n = 1, 2, 3, 4 etc.
3. The wave function Ψ<sub>0</sub>(x) = 0 is NOT allowed.
The last point merits mild elucidation. QM states that bound particles CANNOT be stationary. Even the ‘lowest’ allowed wave function
(Ψ<sub>1</sub>(x) = √(2/L) sin(πx/L) ) is non-zero (except for x = 0 and x = L, of course)
Compare and contrast this with a Classical (non-Quantum) system: you can park your car and it will be stationary (E = 0) but that super small
‘quantum car’ would always be moving in its box! Quantum particles cannot ‘sit still’.
[Edited on 16-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Sorry i'm late sir.
I was in detention all afternoon for holding Zombie's head down the toilet.
So by defining a restricted space, you can eleminate terms from the equation !
I like it.
More please : why cannot the Quantum bits remain still ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Sorry i'm late sir.
I was in detention all afternoon for holding Zombie's head down the toilet.
So by defining a restricted space, you can eleminate terms from the equation !
I like it.
More please : why cannot the Quantum bits remain still ? |
As long as it's not the old CaC2/toilet trick, I'll allow it.
U(x)Ψ(x) drops out because in this specific example U(x) = 0. But derivations for the particle in a box where U(x) is not zero do also exist. I chose
U(x) = 0 because it's the simplest example.
Further down the course I'll show a Java applet that calculates wave functions for many other non-zero U(x) situations. All things in good time
though.
Bound Quantum bits can't sit still because that is a consequence of the SE: Ψ(x) = 0 (for this particular problem!)
is not an allowed solution to it. It's part of the "bizarrerie" that is QP. Take it or leave it! 
A free electron can have v = 0 (E<sub>kin</sub> = 0) but that is a very different situation.
If you think all this is weird, you're right but wait till we get to quantum entanglement! 
[Edited on 19-7-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The Standing Waves Analogy and the probability of finding the particle at location x (Particle in a Box Continued)
Many textbooks use an analogy that helps to ‘concretise’ (i.e. visualise, imagine) the wave functions somewhat. In it the matter waves of the
particle are compared to the standing waves in a musical string (like a guitar string). You can generate and visualise standing waves in a real
experiment by tying one end of skipping rope to a door knob (or such like) and moving the other end up and own with your hand. Get the frequency right
and the skipping rope will take on the shape of Ψ<sub>1</sub>(x). Double the frequency of your hand movement and the pattern will
resemble Ψ<sub>2</sub>(x) etc etc.
In this analogy the particle matter wave resonates like a standing wave in the box’ cavity, like the skipping rope forms a standing wave between the
door knob and your hand.
But remember that moving particles have a dual character: they are both waves and particles at once! Looking inside the box we WILL
find the particle, even though it also behaves like a wave.
We’ve already seen that the probability P (P >= 0 and P <= 1) of finding that particle at location x is given by:
P(x) = ψ<sup>*</sup>(x)ψ(x)
With ψ<sup>*</sup>(x) the Complex Conjugate of ψ(x).
As it happens, we’re in luck! For the particle in a box all ψ<sub>n</sub>(x) are Real functions (ψ(x) returns Real Numbers for any
real x).
And for a real number ψ, then ψ = ψ<sup>*</sup>. Because:
Take a real number ψ and write it as ψ + 0i (“zero times i”). Its complex conjugate is ψ<sup>*</sup> = ψ – 0i.
Obviously in this case ψ <sup>*</sup> = ψ and ψ <sup>*</sup>ψ = ψψ = ψ<sup>2</sup>.
Thus P(x) = ψ<sup>*</sup>(x)ψ(x) = ψ(x)<sup>2</sup> or simply ψ<sup>2</sup>, for Real wave functions.
So quite literally the probability P of finding the particle at location x is:
P(x) = ψ(x)<sup>2</sup>
We can now generalise this for any particle in a one dimensional box. Since as:
Ψ<sub>n</sub>(x) = √(2/L) sin(nπx/L)
It follows that:
Ψ<sub>n</sub>(x)<sup>2</sup> = (2/L) sin<sup>2</sup>(nπx/L) (or (2/L) [sin(nπx/L)]<sup>2</sup>, if
you prefer).
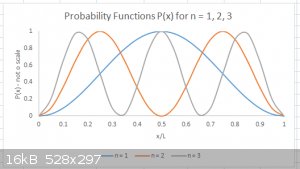
I’ve plotted the Probability function P<sub>n</sub>(x) for n =1, 2 and 3 below. Note that the P(x) values are NOT to scale.
In WM and quantum Chemistry, the points where P = 0 are often referred to as ‘nodes’ and the areas where P > 0 as ‘lobes’.
[Edited on 18-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Erm, can i digest this for a while ?
I have a feeling you'll extrapolate to three dimensions any second now, and it's quite hard for a dullard like me to keep a hold onto this maths
train ride.
Thanks very much for explaining this, and for free.
Edit:
It feels like i should be paying for the time you're putting in to what looks like just My education.
[Edited on 18-7-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Erm, can i digest this for a while ?
I have a feeling you'll extrapolate to three dimensions any second now, and it's quite hard for a dullard like me to keep a hold onto this maths
train ride.
Thanks very much for explaining this, and for free.
Edit:
It feels like i should be paying for the time you're putting in to what looks like just My education.
[Edited on 18-7-2015 by aga] |
Take your time. We'll be staying in 1 dimension for a bit yet.
There will also be even less math in 3D because it's far too complicated for my purpose here.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Thank you.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Just let me know any questions you WILL have and when you're ready to move on.
Did you get Zomb's head out of the toilet pan or is he still smoking behind the gents?
[Edited on 19-7-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by blargish  | | Not exactly sure how correct this is, but the way I usually think of it is that even though something big like a truck has some tiny de Broglie
wavelength, it could never pass through a sufficiently small opening for diffractive effects to occur, and thus its wave character to be even
noticeable, whist electrons and other subatomic particles are on a scale such that these wave-like effects do come into play. |
I know this thread is geared more towards introductory-level physics, so this is probably going to be well beyond the scope of this discussion, but
the reason macroscopic systems like trucks and bullets don't behave like quantum systems is not actually because of their size. All systems,
regardless of size, are inherently quantum systems by nature and thus governed by quantum mechanics. The reason for the emergence of seemingly
classical behavior from otherwise large quantum systems is due to the irreversible loss of coherence through interactions with their environment
(decoherence). Being an open quantum system, the large number of degrees of freedom in the surrounding environment rapidly destroys any quantum
properties of the object. This is why you don't see macroscopic objects in superposition.
By continuously being bombarded with photons and bumping into nearby air molecules and various other atoms/molecules, the truck is constantly being
monitored or "observed" by its environment. The states of the system (the truck) quickly become entangled with the states of the environment,
decohering them from one another and preventing interference. Through a process called einselection, "pointer states" are singled out. These states
are the least prone to entanglement with the environment, and are the ones that remain after decoherence. These surviving states are essentially
"classical states" that continue to persist despite the environmental monitoring, and are why macroscopic objects appear to have definite properties.
Since it's usually the position basis that gets singled out, macroscopic objects tend to be in eigenstates of position. This transformation of a pure
state into an improper mixed state gives the appearance of wavefunction collapse. This is why the truck doesn't exhibit "wavy" behavior.
The reason for classical behavior in macroscopic objects is not simply because of their size, but the difficulty in maintaining coherence in open
quantum systems. A truck will never behave like a wave for this very reason. There are ways, however, such as using extremely cold temperatures, to
slow the decoherence process down long enough to actually see quantum effects in macroscopic objects.
Don't worry, that's perfectly normal. Everyone's lost when they're first introduced to the strange and counter-intuitive world of quantum mechanics.
To be honest, I'd be far more concerned if you weren't. As John Wheeler once said, "if you are not completely confused by quantum mechanics,
you do not understand it."
The irony of it all is that the longer you study QM, the less sense it actually makes. 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Oh goody.
I'm way ahead of the game then !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks Darkstar, that was an interesting interlude.
One can also point to the 'Correspondence Principle' (I might spend a brief moment on it later on) to show that real (small) quantum systems start
behaving 'Classically' for high values of E<sub>n</sub> (high n, in other words). The border between quantum and classical is fuzzy, not
sharp.
Of QP has also been said that if you think you've understood it, that means you've not studied it enough! That might sound like QP is the lunatic
asylum of physics but the 'problem' is that it works and provides real life solutions to real life physical problems! Doh! 
[Edited on 19-7-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Here’s that Java applet that shows energies (eigenvalues) and wave functions for a variety of ‘particle in a box’ situations:
http://www.falstad.com/qm1d/
I have to say that on my tooter it only works in IE, not Google Chrome (it needs some patch, I think)
Select “1-D Quantum Crystal Applet”.
In the new window the applet will start. Right top is a control panel that allows varying settings of the system. From the top drop down menu, select
‘Infinite well’.
In the top box the horizontal lines represent the energy levels (eigenvalues), the ground state is in red.
Mouse-hovering over the energy levels you’ll see the wave functions (in yellow) appear in the middle box.
Moving the slide rulers you can adjust L (box width) and m (particle mass) and observe the changes in E and ψ(x).
Now select ‘Infinite well + Field’ from the top draw down menu. This introduces a U(x) function that is non-zero and linear: U(x) = ux
(with u a constant). Observe the wave functions ψ(x)! Note how the wave function is ‘dampened’ down for larger U values.
Have fun.
[Edited on 19-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Please Sir. Can't see an Infinite Well option Sir.
Got :-
Finite Well
Well Pairs
Couple Well Pairs
Harmonic
Coulomb-like
Free Particle
Sinusoidal
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
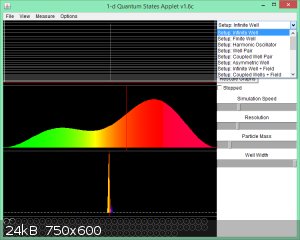
No, I can see it: Set up: Infinite Well
It's the top option: move the right slide bar to the top.
You in IE or another browser?
However, you can look at Finite Well as well. That means the walls are not infinitely high but finitely high.
Screenshot:
[Edited on 19-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
That was Firefox.
Will try IE.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Infinite well with Linear Field: wave function for n = 5:
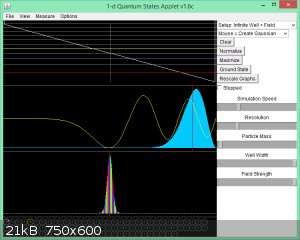
White horizontal lines in top box are E<sub>n</sub> eigenvalues (red is ground state).
White sloped line is U(x) = ux.
Yellow wavy line in second box is Ψ<sub>5</sub>(x).
[Edited on 19-7-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
No problem. Just thought I'd contribute a little to the discussion since you're the only one participating at the moment. I think the idea of a free
and interactive QM course here on SM is an awesome idea, and I'd be more than happy to help you teach. It's very generous of you to donate so much of
your time tutoring others for free, especially when it's just one-on-one (like with aga). It's such a shame that so few here actually seem interested.
| Quote: |
One can also point to the 'Correspondence Principle' (I might spend a brief moment on it later on) to show that real (small) quantum systems start
behaving 'Classically' for high values of E<sub>n</sub> (high n, in other words). The border between quantum and classical is fuzzy, not
sharp. |
True. I actually considered mentioning the correspondence principle in my previous post since it helps to explain why those quantum systems
start behaving classically under certain conditions, not just that they do. But considering the nature of some of the concepts being discussed
(decoherence, entanglement, pure/mixed states, wavefunction collapse etc), any student that has the necessary prerequisites to actually make sense of
what was said would more than likely already be quite familiar with the correspondence principle. For the most part, my post was really just intended
for those who already have a fairly decent understanding of QM, and are ready to move away from the introductory-level "large objects have small de
Broglie wavelengths" explanation for the emergence of classical behavior and on to one that is a bit more advanced (and more accepted) that invokes a
combination of decoherence, einselection and 'classical' pointer states (quantum Darwinism).
So in your example of highly energetic quantum systems behaving classically, decoherence would offer an explanation as to why it happens. The
high-energy system is constantly emitting entangled photons in every direction that end up interacting with the surrounding environment and causing
the system to become entangled with it, effectively destroying the superposition (from our point of view, at least) and preventing any further
interference. This also explains why extremely cold temperatures can allow for macroscopic systems to exhibit quantum behavior, as they aren't
emitting entangled photons that would inevitably interact with the environment, allowing them to maintain coherence.
[Edited on 7-20-2015 by Darkstar]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Darkstar:
Thank you. Also for your further elaboration.
'Enrolment' is lower than I hoped for but with now over 1,000 views the thread is probably followed a bit more closely than the number of commenters
might suggest. But it was always going to be a bit of a thankless task.
[Edited on 20-7-2015 by blogfast25]
|
|
|
j_sum1
Administrator
       
Posts: 6333
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
Quote: Originally posted by blogfast25  | | 'Enrolment' is lower than I hoped for but with now over 1,000 views the thread is probably followed a bit more closely than the number of commenters
might suggest |
Hey, I'm thankful. I haven't had much time to go over this closely but I have been reading and following some links. The java applet is not making
its way through the aggressive firewall operational at work so I haven't had a decent play with the parameters. I think however you might be building
a nice compact little tutorial here and one that I will pass on to y physics teacher colleagues.
Just because I m not vocal, don't assume I am not involved.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks, j_sum1, appreciated!
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
It is necessary to Speak before the OP can know anything about your thoughts.
Thank you for doing so.
The notion that a member such as blogfast25 was investing the Time and Effort to teach just the Forum Drunkard was a bit difficult.
[Edited on 20-7-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Another quick tip re. the quantum applet :
http://www.falstad.com/qm1d/
Once you've selected the physical system (infinite well, for instance), from the second drop down menu select 'mouse = set eigenstate'. Also, slide
the 'particle mass' slide rule somewhat more to the left (thereby reducing particle mass and the number of eigenvalues).
This way, when you hover over the top box and click on an eigenvalue (energy E<sub>n</sub> the probability function will also be shown, along with the wave function. the probability function will also be shown, along with the wave function.
The applet also, somewhat inadvertently, demonstrates the Correspondence Principle briefly touched on higher up. If you drastically increase the
particle's mass you'll notice that the energy levels become much closer together. In the limit (for higher and higher values) of m, the energy
spectrum becomes an energy continuum and that is a Classical property. So for very large masses, the particle starts behaving
Classically again. The difference between 'quantum' and 'classical' is not a leap but a fuzzy line in the sand.
[Edited on 21-7-2015 by blogfast25]
|
|
|
MrHomeScientist
International Hazard
    
Posts: 1806
Registered: 24-10-2010
Location: Flerovium
Member Is Offline
Mood: No Mood
|
|
I'm certainly following the thread. Don't be discouraged if there doesn't seem to be much interest up front - in a few months or years, someone might
find this again and be inspired! Despite the lack of commenters, I'm sure many people are avidly reading.
I did have one question from back on page 2, when you said: "QM states that bound particles CANNOT be stationary. "
Could you elaborate on this more? Why exactly is psi = 0 not allowed?
Might it have something to do with the uncertainty principle? If so, I'd think that any particle (bound or unbound) could not be stationary since
you'd know both its position and momentum.
Or perhaps it's because everything possesses wave-particle duality? So the particle is never really 'stationary' because that word doesn't have much
meaning for a wave-like object.
This is probably something I should know, being a physics major and all :/
[Edited on 7-22-2015 by MrHomeScientist]
|
|
|
j_sum1
Administrator
       
Posts: 6333
Registered: 4-10-2014
Location: At home
Member Is Offline
Mood: Most of the ducks are in a row
|
|
Quote: Originally posted by MrHomeScientist  |
Might it have something to do with the uncertainty principle? If so, I'd think that any particle (bound or unbound) could not be stationary since
you'd know both its position and momentum.
Or perhaps it's because everything possesses wave-particle duality? So the particle is never really 'stationary' because that word doesn't have much
meaning for a wave-like object. |
I think these are alternate ways of saying much the same thing. (Please correct me if I am wrong.)
It reminds me of my professor in a course I did on solid state materials (semiconductors et al.) After speaking at length about the Heisenburg
uncertainty principle, he suddenly asked a question on why we never find an electron in the nucleus. Silence from 200 or so electrical engineering
students. He elaborated, "if an electron is negatively charged, it must be strongly attracted to the positive nucleus. You'd think that there would
be a non-zero chance of finding it there." More silence. He then gave us the answer – "Because then we'd know where it is!"
Well, it was funny at the time. I don't suppose it types up very well.
It was then that the penny dropped for me. The uncertainty principle is not about our inability to find stuff and figure it out. It is about a
genuine inability for objects to occupy a precise location or have zero velocity. It necessarily implies wave-like behaviour for quantum particles.
I have had to retrain my brain in the way I think about electrons and their orbitals. I can't think of them as dots buzzing around randomly like
spastic bees. Rather I have to think of them as being like waves in an aquarium of a particularly weird shape.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by MrHomeScientist  | I'm certainly following the thread. Don't be discouraged if there doesn't seem to be much interest up front - in a few months or years, someone might
find this again and be inspired! Despite the lack of commenters, I'm sure many people are avidly reading.
I did have one question from back on page 2, when you said: "QM states that bound particles CANNOT be stationary. "
Could you elaborate on this more? Why exactly is psi = 0 not allowed?
Might it have something to do with the uncertainty principle? If so, I'd think that any particle (bound or unbound) could not be stationary since
you'd know both its position and momentum.
Or perhaps it's because everything possesses wave-particle duality? So the particle is never really 'stationary' because that word doesn't have much
meaning for a wave-like object.
This is probably something I should know, being a physics major and all :/
|
For one, ψ = 0 also means ψ<sup>2</sup> = 0! Zero probability of finding the particle... And since as P = 0 also outside the box, this
means effectively: NO PARTICLE, whatsoever!
This has also been confirmed empirically: even before QP we knew that the hydrogen atom has a lowest state of energy (the Ground State) that is not
zero (see Bohr's Model and Rydberg).
In the hydrogen atom's ψ<sub>1</sub> corresponds to E<sub>1</sub>, the Ground State. ψ<sub>0</sub> would be
where the electron has crashed into the nucleus (as predicted by Bohr's model). No wave function means no atom!
Thanks for reading!
Thanks also j_sum1, that is correct. There's more than one way of skinning a cat here!
[Edited on 22-7-2015 by blogfast25]
|
|
|
| Pages:
1
2
3
4
5
..
33 |