lacrima97
Hazard to Self
 
Posts: 93
Registered: 24-7-2005
Location: MS
Member Is Offline
Mood: experimental
|
|
Pi, what is it?
My father told me that Pi was 22/7, but I have come to learn that this is just not true. Does anyone know of an exact equation that represents Pi, or
how it is actually found? I am thinking it has to do with the physical measurement of the parts of the circle...
|
|
|
12AX7
Post Harlot
    
Posts: 4803
Registered: 8-3-2005
Location: oscillating
Member Is Offline
Mood: informative
|
|
Lemme see here, what was that...
Pi cannot be expressed by any finite length polynomial. Thus, pi is transcedental. This can be proven (I've never read the proofs). As such, you
also cannot find something as simple as the ratio between the diameter (or radius) and circumference of a circle by ruler-and-dividers means
(geometry). The definition of pi is the ratio of circumference to diameter of a circle.
There are a number of ways you can calculate it. The most common is an infinite Taylor series expansion of a function such as atan(x), setting x = 1
which yields 1 = tan x = sin x/cos x, x = 45 degrees, or pi/4 radians. Generic Taylor series tend to converge slowly, but creative use of constants
can drum out a few digits in the decimal system in only a few terms.
Geometrical methods involve calculating the limit of the circumference of an inscribed and circumscribed regular polygon, increasing number of sides n
--> infinity. (Clearly, a regular polygon inside a circle, with all points on the circle, must have circumference less than the circle, while a
regular polygon outside the circle, so that all sides contact the circle on a tangent, must have a circumference greater. Further, as the number of
sides increases, the difference between the two polygons decreases as they both appear more like the circle.) Obviously, this would converge slowly
depending on your accuracy, but if you make an equation expressing the limit, you can get it in one calculation. Problem: that equation must involve
either an infinite polynomial (because pi is transcedental), or one or more trigonometric equations, which reduce to the same form if the Taylor
theorem is applied.
More creative methods include statistical evaluations. For instance, you can use a perfectly random distribution of statistical events over an area
and count how many land inside a circle of radius R = 1 compared to a square with sides of length 1 or 2 (the latter case would make the square
circumscribed if centered over the circle). Since the statistical 'flux' is equal over the whole area, the counts will be proportional by the area.
The area of a circle is pi * R^2, while the area of a circumscribed square is (2R)^2, or 4R^2. Thus, the ratio of counts yields pi/4.
Another statistical evaluation consists of pi involves calculated propabilities that involve pi. There is a propability of, I believe, throwing a
stick onto a surface marked with parallel lines, and the chance is of landing on one line or no lines, as a function of stick length and line
seperation, or something to that effect. Somehow pi is involved, so by making measurements of large (representative) samples, you can find pi to a
certain accuracy. It is said that well chosen variables can cause the problem to converge to many digits in only several throws, but you know that's
just cheating. 
Note that statistical methods take horribly long to converge properly, since, for perfectly random events, the maximum level of confidence is n^0.5.
Since the square root function is only slowly increasing, you get more accuracy for very large counts.
I once wrote a QuickBasic program that uses the built-in pseudorandom number generator to place points randomly and count hits within a circle. As I
recall, it took about 10 billion counts (a few hours' run time since QB is so slow..) to get five digits or so accuracy. Pretty reasonable figure of
statistics, considering the maximum error is then sqrt(10^10) = 10^5, or 5 decimal points.
Tim
|
|
|
Mr. Wizard
International Hazard
    
Posts: 1042
Registered: 30-3-2003
Member Is Offline
Mood: No Mood
|
|
Here is an interesting site:
http://people.bath.ac.uk/mss20/history.htm
The section on Leonard Euler 1750 has an infinite series that is easy to visualize and even do by hand or with a calculator.
|
|
|
neutrino
International Hazard
    
Posts: 1583
Registered: 20-8-2004
Location: USA
Member Is Offline
Mood: oscillating
|
|
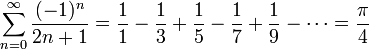
|
|
|
Nerro
National Hazard
   
Posts: 596
Registered: 29-9-2004
Location: Netherlands
Member Is Offline
Mood: Whatever...
|
|
Just as a slight sidenote 22/7 comes pretty close and is a usefull rule of thumb if you have to calculate stuff of the top of your head.
multiplying by 22 and deviding by 7 is just easier than multiplying by 3.14159 
|
|
|
lacrima97
Hazard to Self
 
Posts: 93
Registered: 24-7-2005
Location: MS
Member Is Offline
Mood: experimental
|
|
Ah...I can understand the sin,cos,tan and such, but alot of these things are just over my head.  , Oh well, thanks alot, now I at least know that pi is more complex than 22/7. , Oh well, thanks alot, now I at least know that pi is more complex than 22/7. 
|
|
|
zoomer
Hazard to Self
 
Posts: 66
Registered: 22-3-2005
Location: Watching the sun set over the saguaros
Member Is Offline
Mood: Always Curious
|
|
I've always wondered, is there a radix in which pi is rational?
|
|
|
chromium
Hazard to Others
  
Posts: 284
Registered: 27-6-2005
Member Is Offline
Mood: reactive
|
|
pi = 3.1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
3809525720 1065485863 2788659361 5338182796 8230301952
0353018529 6899577362 2599413891 2497217752 8347913151
5574857242 4541506959 5082953311 6861727855 8890750983
8175463746 4939319255 0604009277 0167113900 9848824012
8583616035 6370766010 4710181942 9555961989 4676783744
9448255379 7747268471 0404753464 6208046684 2590694912
9331367702 8989152104 7521620569 6602405803 8150193511
2533824300 3558764024 7496473263 9141992726 0426992279
6782354781 6360093417 2164121992 4586315030 2861829745
5570674983 8505494588 5869269956 9092721079 7509302955
3211653449 8720275596 0236480665 4991198818 3479775356
6369807426 5425278625 5181841757 4672890977 7727938000
8164706001 6145249192 1732172147 7235014144 1973568548
1613611573 5255213347 5741849468 4385233239 0739414333
4547762416 8625189835 6948556209 9219222184 2725502542
5688767179 0494601653 4668049886 2723279178 6085784383
8279679766 8145410095 3883786360 9506800642 2512520511
7392984896 0841284886 2694560424 1965285022 2106611863
0674427862 2039194945 0471237137 8696095636 4371917287
4677646575 7396241389 0865832645 9958133904 7802759009
9465764078 9512694683 9835259570 9825822620 5224894077
2671947826 8482601476 9909026401 3639443745 5305068203
4962524517 4939965143 1429809190 6592509372 2169646151
5709858387 4105978859 5977297549 8930161753 9284681382
6868386894 2774155991 8559252459 5395943104 9972524680
8459872736 4469584865 3836736222 6260991246 0805124388
4390451244 1365497627 8079771569 1435997700 1296160894
4169486855 5848406353 4220722258 2848864815 8456028506
0168427394 5226746767 8895252138 5225499546 6672782398
6456596116 3548862305 7745649803 5593634568 1743241125
1507606947 9451096596 0940252288 7971089314 5669136867
2287489405 6010150330 8617928680 9208747609 1782493858
9009714909 6759852613 6554978189 3129784821 6829989487
2265880485 7564014270 4775551323 7964145152 3746234364
5428584447 9526586782 1051141354 7357395231 1342716610
2135969536 2314429524 8493718711 0145765403 5902799344
0374200731 0578539062 1983874478 0847848968 3321445713
8687519435 0643021845 3191048481 0053706146 8067491927
8191197939 9520614196 6342875444 0643745123 7181921799
9839101591 9561814675 1426912397 4894090718 6494231961
5679452080 9514655022 5231603881 9301420937 6213785595
6638937787 0830390697 9207734672 2182562599 6615014215
0306803844 7734549202 6054146659 2520149744 2850732518
6660021324 3408819071 0486331734 6496514539 0579626856
1005508106 6587969981 6357473638 4052571459 1028970641
4011097120 6280439039 7595156771 5770042033 7869936007
2305587631 7635942187 3125147120 5329281918 2618612586
7321579198 4148488291 6447060957 5270695722 0917567116
7229109816 9091528017 3506712748 5832228718 3520935396
5725121083 5791513698 8209144421 0067510334 6711031412
6711136990 8658516398 3150197016 5151168517 1437657618
3515565088 4909989859 9823873455 2833163550 7647918535
8932261854 8963213293 3089857064 2046752590 7091548141
6549859461 6371802709 8199430992 4488957571 2828905923
2332609729 9712084433 5732654893 8239119325 9746366730
5836041428 1388303203 8249037589 8524374417 0291327656
1809377344 4030707469 2112019130 2033038019 7621101100
4492932151 6084244485 9637669838 9522868478 3123552658
2131449576 8572624334 4189303968 6426243410 7732269780
2807318915 4411010446 8232527162 0105265227 2111660396...
...and so on
|
|
|
JohnWW
International Hazard
    
Posts: 2849
Registered: 27-7-2004
Location: New Zealand
Member Is Offline
Mood: No Mood
|
|
Thanks, Chromium. Those numerous pi digits, assuming no bias or pattern in them (Pi being both transcendental and irrational), can be used to select
randomly numbered objects for testing or sampling in quality control.
I use ¶ (alt-0182) to represent pi, without using custom fonts.
A much closer approximation to ¶ than 22/7 is 355/113 = 3.1415929 ...., deviating from true only in the 8th digit. This was discovered by the
Chinese mathematician Tsu Ch'ung-Chi hundreds of years ago, and rediscovered by Metius in the 16th century. By use of continued fractions, the next
close approximation to ¶ as a rational fraction is 103993/33102, and after that 1019514486099146/324521540032945
The above series for ¼¶ was discovered by Leibniz in 1673. However, it converges much too slowly to be of much use, and much more rapidly
converging alternatives have been found, usually by such statagems as solving differential equations as Fourier series. Also by the Fourier-series
method, series for powers of ¶ can be found in which the Bernoulli and Euler numbers appear in the numerator with the power of ¶, e.g. ¶²/6 = 1 +
1/2² + 1/3² + 1/4² + .... = zeta(2), and ¶²/8 = 1 + 1/3² + 1/5² + 1/7² + 1/9² + .... , and ¶³/32 = 1 -1/2³ + 1/3³ - 1/5³ + 1/6³
- ....., and ¶^4 = zeta(4) = 1 + 1/2^4 + 1/3^4 + 1/4^4 + ......, etc. Odd powers of ¶ can only be summed as alternating series, and these ones have
the powers as multiples of Euler numbers, as opposed to the Bernoulli numbers in the even-power series.
S> ramanujan found, mostly by geometric arguments, approximations to ¶ involving rational powers of integers. For example: (81 + 361/22)^¼ =
approx. ¶ correct to 10 places;
63(75sqrt5 + 503)/13450 = approx. ¶ to 9 places; and 9801/2206sqrt2 = approx. ¶ to 8 places.
There are approximations involving rational powers of ¶ although threse cannot easily be solved for ¶, e.g. (¶^4 + ¶5)^(1/6) = approx. e
(=2.718281828 ...).
|
|
|
woelen
Super Administrator
        
Posts: 8031
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
| Quote: | Originally posted by zoomer
I've always wondered, is there a radix in which pi is rational? |
Rationality has nothing to do with how a number is represented, it is a property of the number itself. A number does not change if we just use another
notation for that number.
|
|
|
zoomer
Hazard to Self
 
Posts: 66
Registered: 22-3-2005
Location: Watching the sun set over the saguaros
Member Is Offline
Mood: Always Curious
|
|
| Quote: | Originally posted by woelen
Rationality has nothing to do with how a number is represented, it is a property of the number itself. A number does not change if we just use another
notation for that number. |
Doh! I had never put the two together regarding pi, but now that I think "rationally" about it, you are correct. (Gee, I should have asked sooner.)
Sorry! 
Z
|
|
|
Nerro
National Hazard
   
Posts: 596
Registered: 29-9-2004
Location: Netherlands
Member Is Offline
Mood: Whatever...
|
|
It just means there is no function of anything that will give the exact value of pi just approximations
|
|
|
neutrino
International Hazard
    
Posts: 1583
Registered: 20-8-2004
Location: USA
Member Is Offline
Mood: oscillating
|
|
There are numerous functions that will give the exact value, e.g. the one I posted above. The only problem is that they require infinite calculation
to find the numerical value. For all intents and proposes, though (multiplying, dividing, finding the value to x decimal points, etc.), they are
equivalent to pi. For example,
2 * Pi / 4 = 2/1 - 2/3 + 2/5 - 2/7 + … = Pi / 2
|
|
|
Ramiel
Vicious like a ferret
  
Posts: 484
Registered: 19-8-2002
Location: Room at the Back, Australia
Member Is Offline
Mood: Semi-demented
|
|
I always thought the relationship between pi and e was exact?
(pi<sup>4</sup> + <sup>5</sup> <sup>1/6</sup> =
e <sup>1/6</sup> =
e
or what about :
e<sup>i.pi</sup> + 1 = 0
?
never quite understood how two trancendential numbers could be interrelated as it so seems... 
Caveat Orator
|
|
|
Quibbler
Hazard to Self
 
Posts: 65
Registered: 15-7-2005
Location: Trinidad and Tobago
Member Is Offline
Mood: Deflagrated
|
|
Using Euler's formula
e^i*pi = cos(pi)+i sin(pi) = -1
As for pi Machin's method is fairly quick.
|
|
|
Nerro
National Hazard
   
Posts: 596
Registered: 29-9-2004
Location: Netherlands
Member Is Offline
Mood: Whatever...
|
|
Yes that's nice but none of them produces the complete number. When you use thse unctions to calculate pi you always get an approximation.
|
|
|
praseodym
Hazard to Others
  
Posts: 137
Registered: 25-7-2005
Location: Schwarzschild Radius
Member Is Offline
Mood: crazy
|
|
This is because there is no exact value for pi...
|
|
|
woelen
Super Administrator
        
Posts: 8031
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
| Quote: | Originally posted by Ramiel
I always thought the relationship between pi and e was exact?
(pi<sup>4</sup> + <sup>5</sup> <sup>1/6</sup> =
e <sup>1/6</sup> =
e
or what about :
e<sup>i.pi</sup> + 1 = 0
?
never quite understood how two trancendential numbers could be interrelated as it so seems...  |
The first one is not exact. As far as mathematicians know, there is no algebraic (in the sense of fields) relation between e and pi. In other words,
pi cannot be expressed as function of e, using a finite number of radicals, powers, and basic arithmetic operations only.
The second one is exact, but it is not an algebraic relation in the sense of field algebra (there is an imaginary number in the exponent).
|
|
|
JohnWW
International Hazard
    
Posts: 2849
Registered: 27-7-2004
Location: New Zealand
Member Is Offline
Mood: No Mood
|
|
e^(i¶) = -1 is not the only exact relationship between e and ¶, although the others also involve i = sqrt(-1).. There are others derivable from De
Moivre's theorem, e^(ix) = cos(x) + isin(x). Hence, with x = ½¶, e^(½¶i) = i. With x = ¼¶, e^(¼¶i) = ½sqrt2(1 + i) With x = ¶/3, e^(¶i/3)
= ½(1 + sqrt3).
And similarly for powers of multiples of 1/5, 1/6, 1/8, 1/10, 1/12, 1/15, 1/16, 1/17, 1/20, 1/24, etc., of ¶, the trigonometric ratios of which can
be expressed in terms of combinations involving the square roots of the same numbers through the solutions of quadratic equations or of higher
polynomial equations which reduce to combinations of quadratics. The prime numbers in such submultiples of ¶ (1, 2, 3, 5, 17, 257, 65537, etc.) are
"Fermat numbers", 2^(2^n) + 1. However, the next Fermat number after 65537, and all the following ones up to at least the 20th, are NOT prime.
The algebraic insolvability of polynomial equations of the 5th or higher degree (proved by Ruffini and Galois), of course, prevents this for other
submultiples of ¶. The trigonometric ratios of multiples of ¶/7 can be found as the solution of a cubic equation, though.
|
|
|