| Pages:
1
2
3 |
chief
National Hazard
   
Posts: 630
Registered: 19-7-2007
Member Is Offline
Mood: No Mood
|
|
I bet you can't name a single compound that was found by means of your method, right ?
The formulae are adjusted by the properties of the known materials, and that's why those known materials give good results. The adjustment-procedure
is known as "fitting", excessively used everywhere up from engineering (can be done eg. with "gnuplot").
The software-links you named lead to commercial-software-selling-sites, that's suspicious by itself. (Mine too, but for my links there are no
substitutes). ...
Besides: As long as you call me "stupid complacent people" I might as well think of you as an "software-kewl"
Next week we predict explosive power on the x-box-game-console ..
[Edited on 1-10-2008 by chief]
|
|
|
Engager
Hazard to Others
  
Posts: 295
Registered: 8-1-2006
Location: Moscow, Russia
Member Is Offline
Mood: Lagrangian
|
|
Well, now i see who you are, i have no further comments, good luck with self-enjoyment.
|
|
|
chief
National Hazard
   
Posts: 630
Registered: 19-7-2007
Member Is Offline
Mood: No Mood
|
|
Yeah, Thanks ! While I stay critical and don't fool myself I at least can grow on the problem ...
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
C O R R E C T I O N
The expression shown for determining a value for M
as well as the value for M shown , are both in error .
The formula for M as seen in the attached Journal of Chem. Phy. article
shows the middle term , 88 O , of the numerator having a minus sign, that's wrong !
The original Naval Orinance Laboratory ( NOL ) citation depicts this correctly
as positive ( + ) as does the LLLNL Handbook on pg 8.9.
As I had previously done the calculations and saved the work , I just transcribed
that and copied the expressions ( the erroneous one ) from the text. There is
great peril in doing this and not performing cursory checks. I addittionally added ,
instead of subtracting , the rightmost term , 8 H . The correct figure for M is , 34.
M = . . .56 N + 88 O - 8 H . . . = . . . 56( 12 ) + 88( 24 ) - 8( 8 ) . . . = 34
. . . . . . . . 2 N + 2 O + H . . . . . . . . . . 2( 12 ) + 2( 24 ) + ( 8 )
N = ... 2 N + 2 O + H . . . . . . . . . . = . . . .2( 12 ) + 2( 24 ) + ( 8 ) . . . . . . . . . . . . . .≈ 0.03
. . . . 48 C + 4 H + 56 N + 64 O . . . . . . 48( 9 ) + 4( 8 ) + 56( 12 ) + 64(
24 )
The formulas given for M and N intend to acount
for what carbon remains unreacted
in explosives with negative oxygen balance. This does not apply in this case and the
value of M X N = G = calculates to 1.02 , indicating a corrective subtraction of - 6 %
specified on the bottom of page 33 and 35
We now have all the necessary values to calculate this : ( N √ M √ Q )
( Q ( 1 6 3 0 ) is substituteded here without
regard for sign )
( * Note this expression is given as ф ( phi ) in the article ) . . . ( 0.03 ( 5.83 ) ( 40.37 ) ) = 7.06
Detonation pressure = P = 15.58 ρ ² ( N
√ M √ Q )
. . . . . . . . . . . . . . . . . . . . . . . . . 15.58 ( 1.87 ) ² ( 7.06 ) = 3 8 5
kilobars
minus - 24 , 6% correction factor comes to 3 6 2 kilobars
This is comparable to HMX in performance.
Velocity of Detonation = VOD = 1.01 ( 1 + 1.3 ρ
) √ ( N √M √Q)
. . . . . . . . . . . . . . . . .1.01 ( 1 + 1.3 ( 1.87 ) ) √ ( 7.06 ) = 9.208 millimeters per microsecond
multiplied by one million to obtain meters per second ,
minus - 552 , 6% correction factor comes to ≈ 8 6 5 6 Meters / sec
.
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
Using the method of H. H. Cady cited above in LA-7760-MS
on 2,4,6-Tris(trinitromethyl)-1,3,5-triazine , depicted below
Molar . . . . . . . . . . . . . . . Molar
Weight . . . . . . . . . . . . . Volume
46.01 . . . . . . . . . . . . . . 17.02 = NO2
. . . . . . . . . . . . . . . . . . . . +0.54 add correc
. . . . . . . . . . . . . . . . . . . .17.56
. . X 3 . . . . . . . . . . . . . . . . X 3
138.03 . . . . . . . . . . . . . 52.68
+ 12.01 . . . . . . . . . . . . . +3.3 carbon
150.04 . . . . . . . . . . . . . .55.98 trinitromethyl
. . . X 3 . . . . . . . . . . . . . .. . X 3
450.12 . . . . . . . . . . . . .167.94
+ 78.05 . . . . . . . . . . . .+33.73 triazine
_528.7 .X .7 6 8 6 .÷ . 201.67 = 2.013 gm /cc
Density estimate is 5.4 % over actual = 1.91
As no hydrogen is contained , K = .7 6 8 6

The question is raised that
Comparative analysis of this methodology can be made on similar known compounds
with different oxygen balance , such as
2,4,6-Tris( trinitromethyl )-1,3,5-triazine,
which has excess oxygen with no hydrogen , C3 N3 [C( NO2 )3 ]3 => 6 CO2 + 6 N2 + 3 O2
and produces 15 mols of gas per mol
and 2,4,6-Tris( trinitroethyl )-1,3,5-triazine
with oxygen deficiency and hydrogen , C3 N3 [CH2.C( NO2 )3 ]3 => 6 CO2 + 3 CO + 3 H2O + 6 N2
yet produces 18 mols of gas per mol
Wikipedia quotes density to be 1.91 for the tri-trinitromethyl triazine
http://en.wikipedia.org/wiki/2,4,6-Tris(trinitromethyl)-1,3,...
This is the paper cited on the wiki page - that link is dead.
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi...
Synthesis of 2,4,6-Tris(trinitromethyl)-1,3,5-triazine
Mendeleev Communications; Volume 5 (1995), Number 1, Pages 17-18
http://www.rsc.org/publishing/journals/RC/article.asp?doi=rc...
Nitro derivatives of 1,3,5-triazine: synthesis and properties
Russ. Chem. Rev., 2003, 72, pages 279 - 287
http://www.springerlink.com/content/f04565p1q5h37r21
Synthesis of N-trinitroethyl derivatives of linear and heterocyclic nitrogen-containing compounds
Russian Chemical Bulletin, Volume 54, Number 5 / May, 2005, Pages 1346-1349
This is an excerpt of this paper above - C L I C K the image to view it larger in another window
[img]http://resources.metapress.com/pdf-preview.axd?code=f04565p1q5h37r21&size=large[/img]
.
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
Rapid and Accurate Estimation of Densities of Room Temperature Ionic Liquids and Salts
Ye, C.; Shreeve, J. M.
J. Phys. Chem. A.; (Article); 2007; 111(8); 1456-1461.
http://pubs.acs.org/cgi-bin/abstract.cgi/jpcafh/2007/111/i08...
Supporting information ( addendum to article ) - free download
Contains useful data
http://pubs.acs.org/subscribe/journals/jpcafh/suppinfo/jp066...
_______________________________________________
Ionic Liquids & Microwave Activation in Organic Reactions
herkules.oulu.fi/isbn9789514287190/isbn9789514287190.pdf
On pg 91 - condensation of pentaerythritol with acetic acid.
Trinitromethane could serve as well but only if it can be done
at lower temperature for safety sake.
A related article
Microwave in Organic Chemistry
stoltz.caltech.edu/litmtg/2003/yeeman-lit-6_11_03.pdf
.
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
| Quote: | Originally posted by franklyn
| Quote: | Originally posted by Microtek
@ Franklyn
In step 3 where you calculate heat of formation, you would also need to know the temperature change in the reaction; if the hypothetical condensation
reaction is endo- or exothermic you would under- or overestimate the heat of formation respectively. |
Yes point taken , but then I'm not a chemist.
Applicable enthalpies can be found in references I'm sure.
But that depth of involvement in thermodynamics is beyond me.
It appears to be endothermic as related compounds.
so won't be too far off. |
It occurs to me that an expedient way to assess the missing enthalpy of reaction ,
is by comparing the average bond energy of disassociated bonds of the reactants
to the formed bonds of the products.
Using this source > http://www.cem.msu.edu/~reusch/OrgPage/bndenrgy.htm
Thus :
BOND . . . . . C - O . . . H - C . . .
-> . . C - C . . . . O - H
ENERGY . . . 85.5 . . . . 99 . . . .
.-> . . . 83 . . . . . . 111
TOTALS . . . . . . . .184.5 . . . . . . . . . . . . . . . . 194
The difference is 9. 5 Kcal
multiplied by the 4 reaction sites, comes to 38 Kcal / mol reaction enthalpy
If the value for products is less than for reactants then the difference is endothermic
If the value is greater for the products , as in this case , the difference is exothermic
The adjustment is made simply by increasing or decreasing the amount given for the
formation : ∆Hf is + 11.8 kcal /mol is therefore decreased to - 26.2 kcal /mol
As the heat of explosion was overstated by ~ 3.6 % , { 38 / ( 1089 - 38 ) = 38 / 1051 }
all subsequent calculations are similarly diminished.
.
|
|
|
sylla
Alchimiste Belge Notoire
  
Posts: 110
Registered: 2-8-2003
Location: Belgium
Member Is Offline
Mood: No Mood
|
|
Very nice! Really.
A few years ago, I have developped a very same program and model on my own. It's quite nice to see that I used techniques very close to yours.
Unfortunately, I never achieved to make algorithms to predict densities so the program was incomplete (my goal was to make a standalone model, mostly
for educative purposes).
But there are still possibilities to improve your program by a few tricks that can achieve quite nice results actually. (I used to have less than 2%
error on the VOD of RDX, for example, which is so low that it falls in the experimental error range).
Depending on the oxygen balance of the explosive you can use the Kistiakowsky-Wilson or modified Kistiakowsky-Wilson rules. It is also possible to add
new rules to cover more exotic heteroatoms. For example :
Halogen : X --> HX
Sulfur : S --> SO2
Metals (Na, K etc..) : M --> M2CO3
Metals (Ca, etc...) : M --> MO
But what does actually make the difference is the accuracy in decomposition product. Estimmating the products of reaction using the
Kistiakowsky-Wilson rules is actually a very bad, rough, approximation. However, it is possible to build really nice estimmations using equilibria
(considering there are fast enough to take place in explosion). For example you have :
CO2 + H2 <--> CO + H2O
2 CO <--> C + CO2 (*** important because of the loss of gaz ***)
CO + H2 <--> C + H2O (*** important because of the loss of gaz ***)
.5 N2 + CO2 <--> CO + NO
Again, these equilibria will depend on the temperature but so does the heat released and therefore the temperature! This kind of retroaction loop can
be treated through numerical computations again.
1. First Compute the product using the "simple" rules.
2. Compute the heat of reaction and temperature.
3. Compute the current equilibria values for the given temperature.
4. Apply the equilibria to the reaction products (which is another story yet...)
5. Recompute the heat of reaction and temperature.
6. If the difference between the "old" temperature and the "new" one is greater than a given epsilon (about 10°C), go back to step 3.
This is computationaly more expensive than applying the dichotomial algorithm on the temperature profile. But it worth the trial and can be done in a
few ms on a modern computer.
Again, there is yet another possibility to improve the program. By approximating a compound of various explosive as being linear/ideal (ie: there is
no modification by blending two explosive with density d1 and d2, the resulting density being computed directly from d1 and d2 alone), it is possible
to compute the best ratio of two (or more) components.
For example, if we would mix gasoline and air the program would have detected that the most powerful concentration ratio would not have been the
stoichimetric one but, let's say, something that has x% more gasoline. When I worked on my software, years ago, I managed to compute the "best"
(theoretical) ratio for mix such as H2/O2 (which is not the stoichiometric ratio again!) or NH4NO3/TATP and so on. What was actually missing in my
work was that I had too little experimental data to compare with the theoretical one... Though the laters did match what could be read on forums from
experience.
[Edited on 13-2-2009 by sylla]
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Sorry to pose my question so late.
So it is: is this possible to predict the chemical stability via computing way?
[Edited on 3-9-2009 by stid]
|
|
|
Polverone
Now celebrating 21 years of madness
        
Posts: 3186
Registered: 19-5-2002
Location: The Sunny Pacific Northwest
Member Is Offline
Mood: Waiting for spring
|
|
Quote: Originally posted by stid  | Sorry to pose my question so late.
So it is: is this possible to predict the chemical stability via computing way?
|
It's considerably more involved, but I think the answer is yes. See for example this example which uses computational methods to explain the sensitivity of PETN's silicon analog.
PGP Key and corresponding e-mail address
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Thank you for the answer! And one question again: does some strict relation exist between the symmetry of the molecule and the chemical stability of
the substance?
|
|
|
Plasmapyrobattics
Harmless

Posts: 10
Registered: 29-12-2008
Member Is Offline
Mood: Plasma...
|
|
Quote: Originally posted by stid  | | Thank you for the answer! And one question again: does some strict relation exist between the symmetry of the molecule and the chemical stability of
the substance? |
Not necessarily. It also depends on what you mean by “chemical stability”. Do you include sensitivity perhaps?
One finds various symmetrical energetic compounds exhibiting both sensitive, stable and (or) insensitive and/or unstable properties. Examples are :
1. 5,5-bis(nitrotetrazole) [very sensitive but relative stable].
2. 4,40-dinitro-3,30-azo-bis(furazan) [sensitive but relative stable].
3. octahydro-1,3,4,6-tetranitro-3aa,3bb,6ab,6ba-cyclobuta(1,2-d:3,4-d0)-diimidazole-2,5-dione [sensitive but relative stable].
4. 2,6-diamino-3,5-dinitropyrazine [relative insensitive and stable].
5. 3,30-azo-bis(6-amino-1,2,4,5-tetrazine) [relatively insensitive and stable].
6. cissyn-cis-2,6-dioxo-1,4,7,8-tetranitrodecahydro-1H,5H-diimidazo(4,5-b:40,50-e)pyrazine [relative insensitive and stable].
7. 1,3,4,-tetranitroglycouril [medium sensitivity and relatively (hydrolytically) unstable].
Hope this helps
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Hi,
I have calculated the density of HMX using the correction coefficient 0,955. The obtained density is 1,83 gr/cm3– very different from the
experimental value. But the no corrected value is very close – 1,91 gr/cm3. What happens? And what is the relation between the pm3 optimized
structure of HMX and his different real isometric structures?
Thanks
|
|
|
simply RED
Hazard to Others
  
Posts: 209
Registered: 18-8-2005
Location: noitacoL
Member Is Offline
Mood: booM
|
|
PM3 is semiempirical method. The geometry optimized with it has nothing in common with the experimental one. Semiempirical methods give tremendous
errors when computing nitramines' properties with them. They are not parametrized for this kind of compounds.
Try ab-initio methods.
RHF with 6-31G gives good geometry and bond lengths similar to X-ray analysis.
DFT (B3LYP), MP2... Should give good results too.
When logic and proportion have fallen sloppy dead...
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Thanks for your answer!
|
|
|
simply RED
Hazard to Others
  
Posts: 209
Registered: 18-8-2005
Location: noitacoL
Member Is Offline
Mood: booM
|
|
One else thing to post : the energy, calculated with semiempirical method or RHF is WRONG. RHF excludes electron correlation and brings error to the
energy. It gives "nice" geometries somehow anyway...
It should be calculated at least with B3LYP or MP2, that you could believe in it. When calculating energy - use polarisation, diffusion and frequency
corrections. When calculating in crystal (multiple molecules), use ++ , **, freq and BSSE (basis set superposition error) ! At least with 6-31G !
By the way : if you want to calculate some properties of a chrystal, you should start with the X-ray analysis geometry (if you have it)! If you are
calculating properties of a new compound, you obviously have no X-ray to start with...
I know it needs extreme computational resources, but there is no other way !
[Edited on 15-10-2009 by simply RED]
When logic and proportion have fallen sloppy dead...
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by simply RED  |
It should be calculated at least with B3LYP or MP2, that you could believe in it.
[Edited on 15-10-2009 by simply RED] |
Two months later,
Hi!
How can I command PCGAMESS to use B3LYP or MP2? Can I download from somewhere examples input files?
Thank you!
[Edited on 20-12-2009 by stid]
|
|
|
Engager
Hazard to Others
  
Posts: 295
Registered: 8-1-2006
Location: Moscow, Russia
Member Is Offline
Mood: Lagrangian
|
|
$CONTRL MAXIT=50 UNITS=ANGS COORD=CART RUNTYP=OPTIMIZE
SCFTYP=RHF DFTTYP=B3LYP $END
$GUESS GUESS=HUCKEL $END
$BASIS GBASIS=N31 NGAUSS=6 NPFUNC=1 NDFUNC=1 $END
$DATA
5-Nitro-1H-Tetrazole, optimization 63-1G** B3LYP functional.
C1
C 6.0 0.0101202824 -0.0433480092 -0.0646075395
N 7.0 0.8086734648 1.0941011978 -0.0948870086
N 7.0 2.0860823587 0.7103841160 -0.0935010466
N 7.0 2.1224873963 -0.5835695032 -0.0644757289
N 7.0 0.9068321991 -1.0745229357 -0.0464345781
N 7.0 -1.4875960040 -0.1257062031 -0.0542365103
O 8.0 -2.0397093943 -1.1913111230 -0.0261163789
O 8.0 -2.0665188892 0.9431247185 -0.0759871348
H 1.0 0.5390141506 2.0473502898 -0.1149126989
$END
|
|
|
stid
Harmless

Posts: 6
Registered: 3-9-2009
Location: Bulgaria
Member Is Offline
Mood: No Mood
|
|
Thank you!
I will try.
The input coordinates of your example is the coordinates given of MM2 optimization of Chem3D?
[Edited on 20-12-2009 by stid]
|
|
|
Engager
Hazard to Others
  
Posts: 295
Registered: 8-1-2006
Location: Moscow, Russia
Member Is Offline
Mood: Lagrangian
|
|
Calculating brisance or shattering effect
Brisance is the destructive fragmentation effect of a charge on its immediate vicinity. When an explosive detonates,
tremendous pressure is released practically instantaneously in a shock wave which exists only a fraction of a second at any given place. The
subsequent expansion of gases performs work but the sudden pressure thus created will shatter rather than displace any object in its path. The ability
of an explosive to demolish (fragment, shatter) a solid object (such as steel, concrete, stone) when fired in direct contact with it or in its
vicinity is called brisance (from the French "briser" = to break or shatter). From a military viewpoint brisance is of practical importance because it
determines the effectiveness of an explosive in fragmenting shells, bomb casings, grenades, mines, etc and in imparting high velocities to the
resulting fragments. As the shattering effect is dependent upon the suddenness with which the gaseous products of an expl are liberated, the velocity
of detonation is at least a major factor in determining.brisance. It has been found that there is a general linear relationship between velocity of
detonation and brisance, and if the velocity is known it is possible to calculate the brisance or vice versa (as will be shown below under
Brisance-Detonation Velocity Relationship)Brisance may also be calculated from the formula of Kast (see below) or determined experimentally by one of
the test methods. Since brisance is approx proportional to detonation velocity, “force” and density of loading, Kast proposed to determine
it by the following equation:
B = F * d * D
Where В is brisance value (BrisanZwert in Ger), d is density of charge, D detonation velocity in m/sec and F
"specific energy or force", also called “specific pressure”. The Germans call it "spezifische Kraft oder Energie". The force is expressed
in kg/cm and is equal to p0 * v0 * T/273 where p0 is atmospheric pressure expressed as 1.033kg/cm2, v0 volume of gases developed on explosion in cc
per g of explosive, reduced to 0C and 760mm Hg pressure and T is the max absolute temperature of explosion. On substituting for F, in the above
expression, the following equation is obtained:
В = P0 * v0 * T/273 * d * D
In the above equation T is equal to t+273 or to Qe/C + 273 where Qe is the heat of explosion in cal/g and C is the
mean specific heat of the products of expln in cal/g. As an example, for blasting gelatin (NG 92 & NC 8%), Stettbacher gives: p0 = 1. 033, v0 =
711.4cc per g, T = 4410°C, d 1.60 and D = 7500 m/sec. This gives:
B= 1.033*711.4* (4410/273) * 1.6 * 7500 = 151.2E+6
Kast's values for many explosives can be found in references. However, practical tests do not confirm the idea that
В is proportional to the square of the deton velocity but that simple proportionality (as in the formula of Kast) agrees better with the facts.
Friederich introduced the term "specific brisance" and proposed to calculate it from the formula (D2max*A)/100 kg/cm2, where Dmax is detonation
velocity and A specific gravity in g/cc. The following table compares "specific brisance" with Kast's brisance values:

It should be noted that brisance is a very complicated phenomenon and that none of the existing methods of
calculation, such as by Kast's formula (see above), Herlin's formula, Bichel's formula, Friederich's formula, etc or of experimental determinations
gives exact interpretation of B. The matter of detg it is complicated by the fact that the В of a cartridge of explosive is different in
different directions: if a cylindrical cartridge is detonated from one end, the action in the direction in which detonation proceeds is considerably
greater than that in the opposite direction. According to Cook the term brisance was used to describe the property now attributed to detonation
pressure. This property may in many cases be calculated from fundamental physical laws. For a condensed explosive the detonation pressure p2 may be
approx calcd from the equation:
p2 = 0.00987*p*(D^2)/4
Where p, is the original density and D the detonation velocity in m/sec. A more accurate equation is also given by
Cook. Lothrop & Handrick discussing the relationship between performance and constitution of pure organic compounds included curves showing the
relationship between power & brisance and oxygen balance of many organic explosives. Price, in discussing the dependence of damage effects upon
detonation parameters of organic high explosives, substituted the term detanation pressure for brisance and detonation energy for power. She also
stated that from data obtained at NOL, it has been possible to show that fragment velocity, shaped charge penetration, airblast, and underwater
effects are related to the explosive properties of detonation pressure and detonation energy.
Brisance-Detonation Velocity Relationship.
Brisance-Detonation Velocity Relationship has long been recognized that brisance is related to detonation velocity
and efforts have been made to determine and express relationship beween these two characteristics of an explosive. According to Rinkenbach, there was
developed at Picatini Arsenal the following approx empirical relationship between brisance(B) in grams of sand crushed by 0.4g sample when detonated
in a 200-g bomb, and detonation ve-locity (D) in m/sec; logB= 3.451og(D/2450). A similar equation was later reported in a manual compiled at Aberdeen
PG. From sand test values (B) detd at PicArsn for ca 20 explosions (using 0.4g samples in both 200g and 1700g bombs) and from data available in the
literature for their deton velocities (D) at approx their max densities, Rinkenbach obtained a nearly linear relationship on plotting В vs D.
This permitted the following equations to be derived:
D = 63.99B + 4234 m/sec (for 200-g bomb)
D = 76.76B + 3965 m/sec (for 1700-g bomb)
By means of these equations the detonation velocity of an explosive can be calculated with a mean accuracy of ca 45
m/sec. Note: The above equations are not identical because the values for В obtained in the 1700-g bomb were somewhat lower than those obtained
for the same expls in the 200-g bomb; but the relative orders of the expls with respect to В were the same in both bombs. The difference between
the В values for each explosive in the two bombs is attributed to the different thicknesses of the layers of sand between the cap (contg the
chge) and the walls of the two bombs. Table below gives a comparison between D calcd by Rinkenbach and D obtained by averaging the various values in
the literature.
To calculate brisance of unknown compounds as discussed in this topic one can simply use above equations provided by
Rinkenbach:
B = (D – 4234) / 63.99 (200g bomb)
B = (D – 3965) / 76.76 (1700g bomb)
Using calculated VOD, for example in out test case we get (8899-3965)/76.76 = 64g of crushed sand, experimental
value for RDX at density slightly lower then TMD is 59g of crushed sand. As seen in this example, equations above can provide quite accurate
prediction of brisance.
Explosive Blasting Force
Power of Explosives. In its normally used context, power of an explosive is a misnomer. It is generally accepted
that power of an explosive is a measure of its strength, its blasting action or available energy, and not necessarily a measure of its rate of energy
delivery, which is indeed the true definition of power. Further confusion arises because another frequently used explosives term, called brisance, is
sometimes erroneously equated with power. Brisance is a measure of the ability of an explosive to shatter material in its immediate vicinity. The
fundamental property of an explosive that determines brisance is its detonation pressure. The power of an explosive (we bow to accepted usage and
will keep referring to power rather than the correct terms such as strength or blasting ability), on the other hand, is a measure of the ability of an
explosive to do work such as blasting down rock or propelling a chunk of metal. The fundamental explosive property that determines its power (or
better, available work) is its heat of detonation, Q, or the related quantity, njTj, where nj is the number of moles of gas under steady
(Chapman-Jouguet) detonation conditions and T; is the detonation temperature. As will be shown below, a more exact dependence is that power is
proportional to Q-q (rather than just Q), but q, the residual heat of the detonation products, is usually quite small compared to Q. According to
Andreev & Belyaev, taking to account that exposion process is substantialy adiabatic, the energy available to do external work (we continue to
miscall it power) is:

Where P - pressure, V - volurne, T - ternperature, Cv - specific heat of the detonation products, and the
subscripts, i & f refer to initial and final states respectively. The initial state is usually taken to be that achieved in a constant volume
explosion, the final state is the state of product expansion, after which no more useful work is available. Final temperature of gasses is not easy to
predict, so to make equation more suitable for actuale use it’s more effective to use ratio of pressures instead of temperatures, so taking to
account equation of state for ideal gas we can derive equation above to the following form:

Where K is adiabatic index (Cp/Cv), witch in common explosion conditions is aproximately 1.28 for diatomic gasses
and 1.17 for triatomic ones. Since gasses will expand until they equalize their pressure with surrounding ambience Pi is simply atmospheric pressure
~1 bar or precisely 101325 Pa. Pf – is initial pressure of expanding gasses, it can be derivated from calculated exposion temperature (watch my
posts about calculation of VOD by Keshwarz method above) and by taking to account the fact that at initial moment all explosion produced gasses occupy
space witch was occupied by initial solid exposive, so initial gas volume is Vi = m/r0, where m – mass of explosive, r0 – loading density.
Since equation of state will include ammount of gasses produced by explosion (Ng, moles of gas per mole of explosive), we should use volume of 1 mole
of explosive from witch this ammount of gasses is produced, so Vi = Mw/r0, where Mw is molecular mass of explosive. Substitution of this values into
equation of state for ideal gas (written for Ng moles of gas produced by explosion) gives us following equations:

Here Pi – initial gas pressure (Pa), Pf – ambient pressure (101325 Pa), R – universal gas constant
(8.31), Ng – moles of explosion gasser per mole of explosive, Ti = Te = temperature of exposion (K), Mw – molecular mass of explosive in
(kg/mole), r0 – density of explosive (kg/m3), k – average adiabatic index of gaseous explosion products, Qe – heat of explosion
(MJ/kg), A – efferctive work of explosion (MJ/kg), Ne – explosion work efficency coefficent. Using equations above, with explosive density
(calculated as shown in previous posts), number of explosion gasses per mole of explosive (derivated from explosion reaction equation), explosion
temperature (also computed with calculation of VOD by Keshwarz method described in previous posts), we can now simply calculate effective work of
explosion for our model explosive, only additional parameter witch we need to calculate is K – average adiobatic exponent. Let’s look on
our model explosion equation again:
C3N6H6O6 = 3H2O + 3CO + 3N2
As we see 1 molecule of explosive produces 9 moles of gaseous products, from witch 6 moles are diatomic gases, and 3
moles are triatomic ones. Since K is simple average and for diatomic gasess for common explosion conditions k = 1.28 and k = 1.17 for triatomic ones
we calculate average K:
K = (6/9)*1.28 + (3/9)*1.17 = 1.243
For example let’s calculate effective explosion work for out model explosive from previous posts.For our model
explosive we calculated following parameters: T=3731K; r0 = 1.81 g/cm3 = 1810 kg/m3; Ng = 9; Mw = 222.11 g/mole = 0.2221 kg/mole; Pf = 101325 Pa ; Qe
= 5.668 MJ/kg (more accurately calculated using computed heat of formation for our model exlosive and experimental ones for explosion gasses); R =
8.31 ; K = 1.243, we get:
Ne = 1 - ((101325*0.2221) / (9*8.31*3741*1810)) ^ (0.243/1.243) = 1 - ((22504.2825) / (506418795.9))^(0.1954) = 1 – 0.1411 = 0.858 = 85.8%
A = Ne*Qe = 0.858*5.668 MJ/Kg = 4.868 MJ/kg
Values taken from literature are 86.6% and 4.710 MJ/kg respectively, so computed results are in nice agreement. For
example, below are corresponding values for some commonly used exposives, against their heats of explosion and corresponding ratios vs TNT and results
of Trauzl lead block expansion tests:
Now when we know exposive power we can compare it against corresponting value for some known explosive with known
power test value (for example lead block expansion - Trauzl test) and finaly derivate aproximate test value of explosive power test for our model
explosive. There are many explosive blasting power tests mentioned in literature, three of this methods are in common use: 1) Ballistic Mortar; 2)
Trauzl block expansion; 3) Underwater explosions; and 4) one method - cylinder expansion - that is now used at Lawrence Iivermore Laboratories.
Trauzl Test.
Trauzl Leod Black Test or Lead Black Expansion Test (Cavite au bloc de Trauzl or Epreuve au bloc de plomb de Trauzl,
in Fr) (Trauzlsche Probe or Bleiblockausbachung Methode, in Ger) (Prueba Trauzl or Prueba del bloque de plomo, in Span ) (Metodo del Trauzl or Metodo
del blocco di piombo, in Ital). This test measures the "comparstive disruptive power''of an explosive through enlargement of a cavity in a cylindrical
lead block under carefully standardized conditions. Standart conditions for conducting this test were defined by a Comm. of the Fifth International
Congress of Applied Chemistty. Although one of the oldest tests known for determinating power, it is still widely used today but more common in Europe
than in the USA Scheme of apparatus is shown below:

Procedure. A sample of the test explosive (approximately 10 g) is detonated in a cavity or borehole, 25 mm in
diameter and 125 mm deep, in a standart lead block 200 mm in diameter and 200 mm in height. The borehole is made centrally in the upper face of each
block, previously cast in a mold from desilvered lead of the best quality. An electric blasting cap is placed centrally in the charge. After the
charge and detonator are placed in the borehole, 40 cm3 of Ottawa sand are added and tamped lightly. An additional 10 cm3 of sand are added and tamped
more thoroughly. The volume of the hole made due to the press exerted by the exploding charge is then detd; and the distension(expansion) is
calculated by subtracting from this value, the volume of the borehole before the charge is detonated. Three such tests are made and the results
averaged. Expansions for equivalent weights of explosives are calculated, and the test value is expressed in % of the expansion of an equivalent
weight of TNT. The Trauzl test in France is somewhat different in procedure although dimensions of the lead block are the same. Initiating efficiency
strength of primary explosives can be approximately determinated by firing a small charge (such as 1.0 g) in the cavity of a small lead block, such as
100 mm in height and 100 mm in diam. For testing detonators in such block, a hole is bored in the block of the exact diam of the detonator and of such
a depth that the top of the detonator is flush with the top of the block.
Calculating Trauzl Test Value
As clearly seen from test description above trauzl test results are clearly product of explosive blasting power,
determined by effective work of exposion. To derivate trauzl test results for our model explosive we must compare effective work of explosion of our
explosive against effective work of explosion for some other known explosive with measured Trauzl test. To do so we must enstablish effective work of
explosion equavalency and after that use a graph of Trauzl value vs weight of charge for this known explosive to determine value of Trauzl expansion
for our model explosive. A suitable explosive for comparsion is Ammonite №6, proposed by Andreev & Belyaev due to almost complete
independence of explosion energy from density. Andreev & Belyaev in their book on explosive theory provide the following graph:

Let’s estimate Trauzl Block test value for our modell explosive, to do so the only thing we need is value of
effective work of explosion, witch we calculated in section earlier, for our model explosive (RDX) we calculated Ae = 4.868 MJ/kg ; using data from Ae
table in corresponding section we find Ae for ammonite №6 Ae = 1030 ccal/kg = 4.312 MJ/kg. After subdivision of corresponding values we can
calculate our explosive/ammonite6 eq. ratio and calculate corresponding Trauzl test estimate value for our explosive:
Ae/Ae(ammonite) = 4.868 / 4.312 = 1.128; Eq.w.(ammonite6) = 10*1.128 = 11.28g
Using graph above we get Trauzl test value for our explosive, aproximately 480 cm3, experimental value for RDX is
495 cm3, so method is usefull and can provide results with good align with experiment.
In addtion to this descriptions i have modified detonation calculator utility, now it also calculates effective work of explosion and computes
brisance and blasting power values.
Also i've added blast wave calculator module witch use Sadovsky formula to calculate excessive pressure in front of blast wave at requested range from
explosive charge, using heat of explosion and explosive mass. In addition it creates a report, showing effects of this explosive charge vs uncovered
human and buildings on different distances, calculating hazard radiuses for several types of dammage effects. Theory of blast wave computation will be
posted in this thread some time later when i will have more free time.
[Edited on 7-1-2010 by Engager]
Attachment: Detonation Utility.rar (46kB)
This file has been downloaded 1085 times
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
Very good work Engager , physical performance of explosive materials is a
topic which yet remains to be adequately expressed from calculation alone.
Characteristics that will yield good performance are understood, but are not
easily estimated computationally.
Your utility applying such methods gives essentially the same results for the
hypothetical compound I proposed here , corroborating that the estimate is
correct.
http://www.sciencemadness.org/talk/viewthread.php?tid=11195&...
Attached below the output of your latest Detonation Utility.
Detonation Utility by Engager
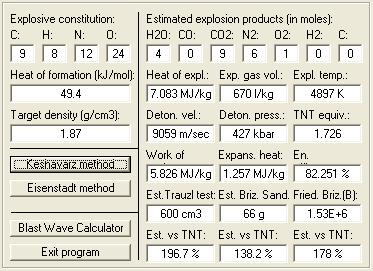
Keshavarz = 9059 , Eisenstadt = 8631
Velocity of Detonation calculated by :
M.J. Kamlett,
S.J. Jacobs = 9208 - 6% correction = 8656
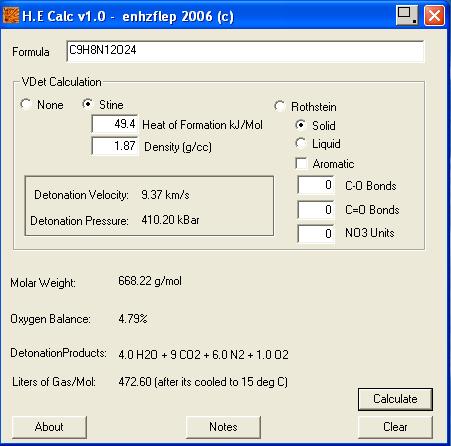
HE calc by enhzflep = 9370
http://www.sciencemadness.org/talk/files.php?pid=64852&a...
___________________________________
@ Engager
Your utility is easy to implement if one understands what the labels ask
but there are subtle issues that I only now discovered which are not
apparent and kept me from applying the earlier version before.
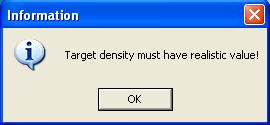
When the utility is initialized the space for " Target density (g/cm3) "
contains an entry which has a coma after the first digit ( 1, ). If one
replaces the 3 digits to the right after this coma ( ,816 ) and runs the
program , a window (attached below) asserting
" Target density must have realistic value " is displayed.
The program will not run for any value greater than ( 1 ).
For the program to work at all for density values greater than ( 1 )
the coma of the initial entry must be deleted and replaced with a period.
.
|
|
|
Engager
Hazard to Others
  
Posts: 295
Registered: 8-1-2006
Location: Moscow, Russia
Member Is Offline
Mood: Lagrangian
|
|
Quote: Originally posted by stid  | Thank you!
I will try. The input coordinates of your example is the coordinates given of MM2 optimization of Chem3D?
|
I don't remember where i taken them, but it's probable that i used common way Chem3D => Gamess RHF, mini basis for initial low cost optimization
=> coords for heavier 6-31G basis set. Sometimes i want even more precise results and use wide basis with extremely computational costly MSCSF
(Multi-configurational self-consistent field), starting on orbitals provided by 6-31G.
Quote: Originally posted by franklyn  | Your utility is easy to implement if one understands what the labels ask
but there are subtle issues that I only now discovered which are not apparent and kept me from applying the earlier version before.
When the utility is initialized the space for " Target density (g/cm3) " contains an entry which has a coma after the first digit ( 1, ). If one
replaces the 3 digits to the right after this coma ( ,816 ) and runs the program , a window (attached below) asserting " Target density must have
realistic value " is displayed. The program will not run for any value greater than ( 1 ).
For the program to work at all for density values greater than ( 1 ) the coma of the initial entry must be deleted and replaced with a period.
|
Thanks, now i finally understand the nature of this problem - it's in locale metrics setting in windows. Here in Russia we use "," to separate number
from fractional part, but in US locale "." is used to do the same. If i run program on my machine and try enter "1.87" it results in error, because
programming language (Visual Basic 6) misinterpreted such input due to my Russian locale setting in windows in witch "," is separator for fractional
part - for VB in my locale value "1.87" is not interpreted as numeric !!!. That's why density "1,87" is shown on initialization. However i don't quite
sure with locales use "," and witch use ".", how can i place correct initialization value then i don't know locale at witch my utility will run?
Franklyn, how do you suggest?
|
|
|
Engager
Hazard to Others
  
Posts: 295
Registered: 8-1-2006
Location: Moscow, Russia
Member Is Offline
Mood: Lagrangian
|
|
Quote: Originally posted by simply RED  | One else thing to post : the energy, calculated with semiempirical method or RHF is WRONG. RHF excludes electron correlation and brings error to the
energy. It gives "nice" geometries somehow anyway...
It should be calculated at least with B3LYP or MP2, that you could believe in it. When calculating energy - use polarisation, diffusion and frequency
corrections. When calculating in crystal (multiple molecules), use ++ , **, freq and BSSE (basis set superposition error) ! At least with 6-31G !
By the way : if you want to calculate some properties of a chrystal, you should start with the X-ray analysis geometry (if you have it)! If you are
calculating properties of a new compound, you obviously have no X-ray to start with...
I know it needs extreme computational resources, but there is no other way !
[Edited on 15-10-2009 by simply RED] |
You are absolutely right, but using costly methods exactly at start it's madness, you will wait for long time (many hours or even days in cases with
big number of atoms or if initial structure guess is bad), especially on heavy basis set... Using PM3 for initial optimization is a generally good
idea, since it fast and WILL converge in most cases. If one needs more precision i recommend to get converged PM3 structure and then => 6-31G + RHF
to get orbitals => MCSCF + MCQDPT. However this will require too much computer time to get this nasty stuff to convege, for general unexperienced
user it is madness, what's why i shown the simplest way first. Advance can always follow.
[Edited on 8-1-2010 by Engager]
|
|
|
franklyn
International Hazard
    
Posts: 3026
Registered: 30-5-2006
Location: Da Big Apple
Member Is Offline
Mood: No Mood
|
|
@ Engager
Programming is something I have only a passing acquaintance with.
I would just use variables to equate coma ( , ) and period ( . ).
coma , ( , ) = Varible ( . ) , period
period , ( . ) = Variable ( , ) , coma
or else
use " go to " command
if ( , ) go to ( action )
if ( . ) go to ( action )
.
|
|
|
Formatik
National Hazard
   
Posts: 927
Registered: 25-3-2008
Member Is Offline
Mood: equilibrium
|
|
thanks again
The program works excellent.
[Edited on 9-1-2010 by Formatik]
|
|
|
| Pages:
1
2
3 |
|