I always thought the relationship between pi and e was exact?
(pi<sup>4</sup> + <sup>5</sup>
 <sup>1/6</sup> =
e
<sup>1/6</sup> =
eor what about :
e<sup>i.pi</sup> + 1 = 0
?
never quite understood how two trancendential numbers could be interrelated as it so seems...


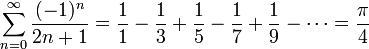

 , Oh well, thanks alot, now I at least know that pi is more complex than 22/7.
, Oh well, thanks alot, now I at least know that pi is more complex than 22/7. 
| Quote: |
| Quote: |

 <sup>1/6</sup> =
e
<sup>1/6</sup> =
e
| Quote: |