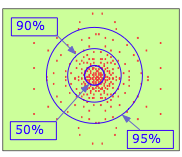

 Regardless, I would suggest that questions of 'what is the case', rather than 'why is the case the case', would be more-likely to yield acceptable
answers, since theories change, yet-- according to one theory(!)-- the facts do not!
Regardless, I would suggest that questions of 'what is the case', rather than 'why is the case the case', would be more-likely to yield acceptable
answers, since theories change, yet-- according to one theory(!)-- the facts do not! 
Quote: Originally posted by quantumchromodynamics  |
| Quote: |
| Quote: |
| Quote: |
Quote: Originally posted by turd  |

Quote: Originally posted by sonogashira  |
Quote: Originally posted by sonogashira  |

| Quote: |