| Pages:
1
2
3 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
All: you're getting warm with Bernoulli.
Fulmen: I love so-called gedanken experiments. Much can be learned from them.
[Edited on 5-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
DOH !
So twelvety thingies is not the right answer ?
No wonder i never got a degree.
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | x^3 would be more understandable.
Thanks for the explanation.
Edit:
So what are the units ?
[Edited on 5-3-2016 by aga] |
I don't have that symbol on my phone key board.
Units means the units of a dimension ie meters are units of length. Newtons are units of force and so on.
Perhaps I answered the wrong question. Do you mean what units you must use in your calculation? If you do then you can can use what ever consistent
units you want. I would use SI units ie meters, seconds, kilograms for mass. Newtons for forces. So bars needs to be converted to Newtons per square
meter.
[Edited on 6-3-2016 by wg48]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Yours is one from the University of Hard Knocks.
Don't knock it!
|
|
|
Metacelsus
International Hazard
    
Posts: 2539
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
The flow velocity at the top of the tank will be 1/3600 the flow velocity through the pipe, from the area ratio.
I've set up the Bernoulli equation:
1/2 * v2 + 3*105 N/m2 / (1000 kg/m3) = 1/2 (v/3600)2 + h * 9.81 m/s2 +
1.3*105 / (1000 kg/m3)
where v is the flow velocity at the bottom of the pipe, and h is the height of the water.
However, I'm getting some odd results with it (imaginary numbers). Did I miss anything?
[Edited on 3-6-2016 by Metacelsus]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Metacelsus  | The flow velocity at the top of the tank will be 1/3600 the flow velocity through the pipe, from the area ratio.
I've set up the Bernoulli equation:
1/2 * v2 + 3*105 N/m2 / (1000 kg/m3) = 1/2 (v/3600)2 + h * 9.81 m/s2 +
1.3*105 / (1000 kg/m3)
where v is the flow velocity at the bottom of the pipe, and h is the height of the water.
However, I'm getting some odd results with it (imaginary numbers). Did I miss anything?
[Edited on 3-6-2016 by Metacelsus] |
The equation look wrong h x 9.81 needs to be multiply by the mass of one cubic meter of water perhaps your missing brackets or I am falling asleep.
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Having thought about the Bernoulli equation is only valid for the pressure at the height of the entry into the tank. As that is not given I can see
no unique solutions. Obviously the height could be ignored but that would be a cheat.
I give up what's the solution then blogfast ???
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by wg48  | Having thought about the Bernoulli equation is only valid for the pressure at the height of the entry into the tank.
I give up what's the solution then blogfast ??? |
Not true at all. The form of Bernoulli's equation to be used is valid at any arbitrary point along the streamline. But you were right in stating one
integration is needed to get a filling time.
You can use Bernoulli to prove Torricelli's Law, e.g. But you need to set it up properly.
I'll publish the solution tomorrow. It's very late here now.
So far Metacelsus has gotten the furthest. But he needs to develop a expression for the volumetric flow rate in function of height of water in the
tank. Your criticism of his equation was wrong though.
woelen was also basically correct.
[Edited on 6-3-2016 by blogfast25]
|
|
|
deltaH
Dangerous source of unreferenced speculation
    
Posts: 1663
Registered: 30-9-2013
Location: South Africa
Member Is Offline
Mood: Heavily protonated
|
|
Nice problem blogfast. My 2.3h is the filling time at a constant dP. So the real answer will be larger. It would be interesting to
see by how much.
|
|
|
Magpie
lab constructor
    
Posts: 5939
Registered: 1-11-2003
Location: USA
Member Is Offline
Mood: Chemistry: the subtle science.
|
|
I converted all pressures to height of water in meters. So the energy balance (Bernoulli eqn) is:
h + 13.3 + (v^2)/2g = 30.6 (eqn 1)
g = acceleration of gravity, 9.81 m/s^2
(v^2)/2g is a loss term for a pipe entrance into a wide opening expressed as a height of fluid.
h is the height of water at any time t (in seconds) and v is the instantaneous average velocity of water in the small pipe in m/s.
V = dh/dt, where V is the instantaneous average velocity in the tank.
v = [(R/r)^2]V, where r and R are radii for the pipe and tank, respectively.
v = [(R/r)^2]dh/dt (eqn 2) (continuity eqn)
Substitute eqn 2 in eqn 1 to eliminate v. Then integrate to definite integrals between h=0 and h=5 and t=0 and t=T. Solve for T the total time.
My solution was T = 16.4 min.
--------------------------------------------------
I know this is not correct as I've ignored the kinetic energy of the incoming stream (v^2/2g) and taken some loss at the entrance which you said to
ignore. But I'll leave it up for discussion.
[Edited on 6-3-2016 by Magpie]
[Edited on 6-3-2016 by Magpie]
[Edited on 6-3-2016 by Magpie]
[Edited on 7-3-2016 by Magpie]
The single most important condition for a successful synthesis is good mixing - Nicodem
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Looking at the problem again and the posts I realize I thought the venturi equation and baliouni equation where the same. Apparently the latter
equation (which I was not familiar with) includes the effects of gravity. That explains some of the posts and blogfast,s comments.
But I am still lost how the entrance pipe can be anywhere other than at the bottom of the tank for a solution.
|
|
|
Fulmen
International Hazard
    
Posts: 1725
Registered: 24-9-2005
Member Is Offline
Mood: Bored
|
|
Actually the solution would be simpler if it were on top, then the back pressure would be constant. With the inlet on the bottom you have to calculate
the increase in back pressure as the level rises. With the inlet anywhere between you'll have to calculate it in two steps, first with constant back
pressure until it reaches the inlet, then with increasing pressure.
We're not banging rocks together here. We know how to put a man back together.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@Magpie:
I like your approach a lot but don't understand where the numbers 13.3 and 30.6 come from. So I haven't checked the integration.
Edit: and I can confirm that plugging in the numbers into your DV, I get:
$$h+660550\dot{h}^2=17.3$$
And integrated between t=0, h=0 and t, h=H I get t = 17.7 min.
Edit 2: oooopsie, now I can see where these numbers come from and where you went a bit wrong.
[Edited on 6-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
My solution:
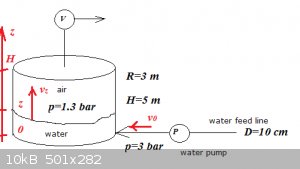
Start from Bernoulli's Equation. Applied here:
$$\frac{v_z^2}{2}+gz+\frac{p_z}{\rho}=\frac{v_0^2}{2}+gz_0+\frac{p_0}{\rho}$$
$$p_z=1.3\:\mathrm{bar}, p_0=3\:\mathrm{bar}, z_0=0$$
Call:
$$p_0-p_z=\Delta p$$
Then:
$$\frac12(v_0^2-v_z^2)=gz-\frac{\Delta p}{\rho}$$
Let:
$$Q$$
... be the volumetric throughput and as water is incompressible, with A the respective cross section:
$$Q=A_zv_z=A_0v_0$$
So:
$$v_z=\frac{Q}{A_z}, v_0=\frac{Q}{A_0}$$
With some reworking we get:
$$\frac12(v_0^2-v_z^2)=\frac{Q^2}{2} \times \frac{A_z^2-A_0^2}{A_z^2A_0^2}$$
Set:
$$\alpha^2=\frac{A_z^2-A_0^2}{A_z^2A_0^2}$$
So:
$$Q(z)=\frac{1}{\alpha}\sqrt{2\big(\frac{\Delta p}{\rho}-gz\big)}$$
So the volumetric throughput is a function of height, as expected. To calculate filling time, note that (with V volume):
$$dV=A_zdz=Q(v)dt$$
Integrate between z=0 and z=H to find total filling time:
$$A_z\int_0^H\frac{dz}{Q(v)}=t$$
$$A_z=\pi R_z^2$$
$$t=\frac{\alpha\pi R_z^2}{\sqrt{2}} \int_0^H\frac{dz}{\sqrt{\frac{\Delta p}{\rho}-gz}}$$
So then:
$$t=\frac{2\alpha \pi R_z^2}{\sqrt{2}g}\Big[\big(\frac{\Delta p}{\rho}\big)^{1/2} - \big(\frac{\Delta p}{\rho}-gH \Big)^{1/2}\Big]$$
Also:
$$R_0=0.05\:\mathrm{m}, R_z=3\:\mathrm{m}$$
$$\alpha=127.4\:\mathrm{m^{-2}}$$
$$\Delta p=(3-1.3) \times 10^5\:\mathrm{Pa}=1.7 \times 10^5\:\mathrm{Pa}$$
$$\rho=1000\:\mathrm{kg/m^3}$$
$$\frac{\Delta p}{\rho}=170\:\mathrm{m^2/s^2}$$
$$gH=49.05\:\mathrm{m^2/s^2}$$
So:
$$t \approx 1050\:\mathrm{s}=17.5\:\mathrm{min}$$
An interesting thing happens when:
$$gH>\frac{\Delta p}{\rho}$$
Then the equation is no longer valid because the square root of a negative number occurs.
$$H=\frac{\Delta p}{\rho g}$$
... is the maximum height to which the pump can still deliver (zero) volumetric throughput, due to hydrostatic pressure of the water column.
[Edited on 7-3-2016 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Wow ! Just Wow.
That's a fine display of mathsiness there bloggers.
Lost me totally at the integration step.
Hey ! 166s = 2.7 somethings !
Incredible co-incidence.
[Edited on 6-3-2016 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Wow ! Just Wow.
That's a fine display of mathsiness there bloggers.
Lost me totally at the integration step.
Hey ! 166s = 2.7 somethings !
Incredible co-incidence.
|
Mathsiness or madness?
You want me to take you through the integration?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Having an idea how do an integration would be wonderful.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Well, for this specific integration:
$$t=\frac{\alpha\pi R_z^2}{\sqrt{2}} \int_0^H\frac{dz}{\sqrt{\frac{\Delta p}{\rho}-gz}}$$
$$t=fI$$
Where f is that composite factor upfront and I is the actual integral. This way we can concentrate on the integral:
$$I=\int_0^H\frac{dz}{\sqrt{\frac{\Delta p}{\rho}-gz}}=\int_0^H\big(\frac{\Delta p}{\rho}-gz\big)^{-1/2}dz$$
Make a substitution:
$$u=\frac{\Delta p}{\rho}-gz$$
Differentiate:
$$du=-gdz$$
$$dz=-\frac1g du$$
The integral now becomes:
$$=-\frac1g \int_0^H u^{-1/2}du$$
This is a tabled integral, so from memory or a table:
$$I=-\frac2g \Big[u^{1/2}\Big]_0^H$$
Substitute back:
$$I=-\frac2g \Big[\big(\frac{\Delta p}{\rho}-gz\big)^{1/2}\Big]_0^H$$
$$I=-\frac2g \Big[\big(\frac{\Delta p}{\rho}-gH\big)^{1/2}-\big(\frac{\Delta p}{\rho})^{1/2}\Big]$$
Invert the sign and multiply with f to get the expression for t in my solution.
[Edited on 7-3-2016 by blogfast25]
|
|
|
deltaH
Dangerous source of unreferenced speculation
    
Posts: 1663
Registered: 30-9-2013
Location: South Africa
Member Is Offline
Mood: Heavily protonated
|
|
I used this online venturi calculator because I'm a lazy shit: http://www.efunda.com/formulae/fluids/venturi_flowmeter.cfm#...
If you do the problem backwards, d=6m pipe constricting to 0.1m pipe and use a constant pressure drop of 1.7bar, I get a fill time of 975s using their
answer of volumetric flow rate of 145l/s, which is much longer than your solution. Considering that I didn't even use it correctly the first time, I
may well be making some stupid mistake again, but try it yourself and if not, perhaps there's a mistake somewhere (could be in their calculator of
course).
Note, the constant pressure drop is just a quick check. The volumetric flow rate with an increasing head should take longer, but not faster, if I'm
not mistaken.
[Edited on 6-3-2016 by deltaH]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by deltaH  | I used this online venturi calculator because I'm a lazy shit: http://www.efunda.com/formulae/fluids/venturi_flowmeter.cfm#...
If you do the problem backwards, d=6m pipe constricting to 0.1m pipe and use a constant pressure drop of 1.7bar, I get a fill time of 975s using their
answer of volumetric flow rate of 145l/s, which is much longer than your solution. Considering that I didn't even use it correctly the first time, I
may well be making some stupid mistake again, but try it yourself and if not, perhaps there's a mistake somewhere (could be in their calculator of
course).
Note, the constant pressure drop is just a quick check. The volumetric flow rate with an increasing head should take longer, but not faster, if I'm
not mistaken.
[Edited on 6-3-2016 by deltaH] |
Thanks delta, will look into it now.
Edit: yup. Spotted an error in alpha. Will correct ASAP.
[Edited on 6-3-2016 by blogfast25]
|
|
|
Magpie
lab constructor
    
Posts: 5939
Registered: 1-11-2003
Location: USA
Member Is Offline
Mood: Chemistry: the subtle science.
|
|
One common form of the Bernoulli equation, which is an energy balance, expresses the energy as "height of fluid." So my pressure terms become
p/density. Then 3bar = 3bar(10.2m/bar) = 30.6m. But you said you had figured that out.
I didn't get going on this problem until late last night but had my solution by 11PM. Then after going to bed I realized my errors and had to get
back up and work on the problem. After going back to bed at 1PM I still had no satisfactory solution. So, thanks for keeping me up all night. 
[Edited on 7-3-2016 by Magpie]
The single most important condition for a successful synthesis is good mixing - Nicodem
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
deltaH was correct.
My value for alpha was way off, due to a silly mistake. 1050 s is in line with the 974 s for the venturi: it's slightly higher due to
gravity (hydrostatic pressure).
[Edited on 6-3-2016 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Magpie  |
One common form of the Bernoulli equation, which is an energy balance, expresses the energy as "height of fluid." So my pressure terms become
p/density. Then 3bar = 3bar(10.2m/bar) = 30.6m. But you said you had figured that out.
I didn't get going on this problem until late last night but had my solution by 11PM. Then after going to bed I realized my errors and had to get
back up and work on the problem. After going back to bed at 1PM I still had no satisfactory solution. So, thanks for keeping me up all night. 
|
Funnily enough that's the form I was taught 30 years ago. But I'm a little rusty.
It kept me up all night too, as I kept finding niggly errors. SORRY! 
|
|
|
deltaH
Dangerous source of unreferenced speculation
    
Posts: 1663
Registered: 30-9-2013
Location: South Africa
Member Is Offline
Mood: Heavily protonated
|
|
Quote: Originally posted by blogfast25  | deltaH was correct.
My value for alpha was way off, due to a silly mistake. 1050 s is in line with the 974 s for the venturi: it's slightly higher due to
gravity (hydrostatic pressure).
[Edited on 6-3-2016 by blogfast25] |
HA, that's nothing, I initially didn't hit the calculate button and worked from the 'default' answer given  of 17l/s of 17l/s 
Very cute problem though, thanks again!
[Edited on 6-3-2016 by deltaH]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Welcome! 
|
|
|
| Pages:
1
2
3 |