| Pages:
1
2
3 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Physics brain teaser: storage tank filling time
A water storage tank is filled by a pump:
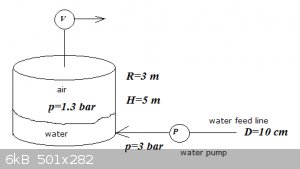
A pump delivers 3 bar of pressure through a 10 cm ID smooth pipe, near the bottom of the tank.
The air venting valve maintains a pressure above the water of 1.3 bar.
The storage tank has a radius of 3 m and height of 5 m.
How long does it take to fill the storage tank?
Hint: ignore viscous losses, drag and inertial effects.
|
|
|
Fulmen
International Hazard
    
Posts: 1725
Registered: 24-9-2005
Member Is Offline
Mood: Bored
|
|
Not enough information, you need pump capacity as well.
We're not banging rocks together here. We know how to put a man back together.
|
|
|
Maker
Harmless

Posts: 46
Registered: 1-11-2015
Member Is Offline
Mood: No Mood
|
|
85 seconds? 
I'm guessing I cocked up somewhere, that sounds insanely small! 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
No, it is sufficient to know the pump delivers 3 bar consistently.
It's teaser, remember?  Not a 'trick question' though... Not a 'trick question' though...
Do provide a modicum of reasoning, please. 
[Edited on 5-3-2016 by blogfast25]
|
|
|
Maker
Harmless

Posts: 46
Registered: 1-11-2015
Member Is Offline
Mood: No Mood
|
|
Sorry, I was typing on my phone and didn't fancy typing all this out;
I used the Hagen–Poiseuille equation, rearranged to equal flow rate;
(Pressure*Pi*diameter^4)/(128*dynamic viscosity*length)=flow rate
I took the pressure to be 170,000 Pa (3-1.3 Bar, it seemed logical but now I have my doubts as to if this is correct  ), the viscosity to be 1PaS * (Water at 20°C) the length to be 1 meter. ), the viscosity to be 1PaS * (Water at 20°C) the length to be 1 meter.
This gave me the seemingly ridiculously high flow rate of 0.417 cubic meters per second. 
Then dividing the volume, 35.3 cubic meters, by the flow rate I got 85 seconds.
*I just went back to check it was the value for 20°C and spotted the unit in the table was PaS x10^-3, I'm three orders of magnitude off!
Using the correct viscosity, I get a flow rate of 417 cubic meters per second! 
Clearly I've done something drastically wrong here, you're probably not even supposed to use that equation. My education in fluid dynamics consists of
about 15 minutes of Googleing after I read the question. Hopefully someone can provide a better answer and explanation. 
[Edited on 5-3-2016 by Maker]
[Edited on 5-3-2016 by Maker]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Maker  | My education in fluid dynamics consists of about 15 minutes of Googleing after I read the question. Hopefully someone can provide a better answer and
explanation. 
|
That explains it then. Still, kudos for trying!  
I'll see if a get a few more takers.
As this derivation will take forever to render in LaTex, I'd better start now though (off site)...
|
|
|
deltaH
Dangerous source of unreferenced speculation
    
Posts: 1663
Registered: 30-9-2013
Location: South Africa
Member Is Offline
Mood: Heavily protonated
|
|
2.3h?
|
|
|
woelen
Super Administrator
        
Posts: 8027
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
I think I need the length of the pipe between the pump and the point where it enters the tank.
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Perhaps the venture effect can be used to determine the velocity in the pipe from the differences in pressure. Using that velocity and the diameter to
of the pipe gives the flow rate which would give the fill time.
It may be complicated by the change pressure at the output of the pipe as the tank fills. Possibly the surface pressure om the water cam be used but
that does not seem valid. Sorry I don,t want to do the actual calculation that's the easy part.
|
|
|
woelen
Super Administrator
        
Posts: 8027
Registered: 20-8-2005
Location: Netherlands
Member Is Offline
Mood: interested
|
|
Quote: Originally posted by wg48  | | [...]It may be complicated by the change pressure at the output of the pipe as the tank fills.[...] |
This
will lead to a differential equation. As the height of the water increases, the pressure at the pipe's entry point at the bottom of the tank increases
from 1.3 to 1.8 bar. So, you can write the pressure difference between pump outlet and tank inlet as a simple function of h, where h is the height of
water, already in the tank.
The time derivative of h can be written as a constant times the inlet flow, the constant depending on the radius of the tank.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The way i see it, the water is leaving a 10cm pipe at 3 bar pressure and entering a 3m pipe at 1.3 bar pressure, just that the pipe going in is at the
side and not in via the bottom.
Not found a forumula to convert that to flow rate yet.
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | The way i see it, the water is leaving a 10cm pipe at 3 bar pressure and entering a 3m pipe at 1.3 bar pressure, just that the pipe going in is at the
side and not in via the bottom.
Not found a forumula to convert that to flow rate yet. |
You can use the venture formular as I suggested above but that would imply the rate is unaffected by the height of the water but that does not seem
valid.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
With the venturi forumla i found, i get the velocity of the water in the tank being the square root of v2<sup>2</sup> - 3.4
still not found the formula to convert pipe diameter and pressure to flow rate or velocity.
[Edited on 5-3-2016 by aga]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by woelen  | Quote: Originally posted by wg48  | | [...]It may be complicated by the change pressure at the output of the pipe as the tank fills.[...] |
This
will lead to a differential equation. As the height of the water increases, the pressure at the pipe's entry point at the bottom of the tank increases
from 1.3 to 1.8 bar. So, you can write the pressure difference between pump outlet and tank inlet as a simple function of h, where h is the height of
water, already in the tank.
The time derivative of h can be written as a constant times the inlet flow, the constant depending on the radius of the tank. |
Yes I agree. But the weakness is the position of the inlet pipe is given as "near the bottom" it seems invalid to assume its at the bottom. The
surface pressure could be used but I don't see how that can be valid either see my other post.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Not needed: all friction losses are ignored, as stated.
Quote: Originally posted by wg48  | | But the weakness is the position of the inlet pipe is given as "near the bottom" it seems invalid to assume its at the bottom. The surface pressure
could be used but I don't see how that can be valid either see my other post. |
Consider the water to come through a pipe in the bottom of the tank, if you want. It makes no difference to the solution of the problem. in my
derivation.
[Edited on 5-3-2016 by blogfast25]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | With the venturi forumla i found, i get the velocity of the water in the tank being the square root of v2<sup>2</sup> - 3.4
still not found the formula to convert pipe diameter and pressure to flow rate or velocity.
[Edited on 5-3-2016 by aga] |
You know know the ratio of v1 and v2 given by the ratios of the pipe to tank diameters.
Ok the maths is a bit more complicated than I originally thought
[Edited on 5-3-2016 by wg48]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Ok so using the ratio of pressures and flow rates we can solve for the file time. I guess the water height effects how hard the pump works but the
flow rate is fixed by the pressure ratios.
But I still have no justification for picking the water surface pressure and not the pressure at the height of the inlet pipe.
We know the rate of energy input given by the rate of the water rising in the tank but I don't see how that helps. Can it be used in a fuller
continuity equation?
[Edited on 5-3-2016 by wg48]
[Edited on 5-3-2016 by wg48]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
From Bernoulli (googled) it seems that the velocity V = square root of (2P/d) where P is differential pressure and d is density (=1) so the velocity
of the flow is sqrt(2P).
This means that the velocity of the water is sqrt(2*1.7) somethings, associated with pounds, inches and square bits.
Flow rate Q = VA, so sqrt(3.4)*pi*1.5*1.5 = 13.03 is the flow rate, in some unknown units involving metres, inches, pounds etc.
The tank's volume is pi*(3/2)<sup>2</sup>*5 = 35.35m<sup>3</sup>
So the tank fills in about 2.71 hours, based on some unknown poundy inchy cuby metre-like unit times hour<sup>-1<sup>
[Edited on 5-3-2016 by aga]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | From Bernoulli (googled) it seems that the velocity V = square root of (2P/d) where P is differential pressure and d is density (=1) so the velocity
of the flow is sqrt(2P).
This means that the velocity of the water is sqrt(2*1.7) somethings, associated with pounds, inches and square bits.
Flow rate Q = VA, so sqrt(3.4)*pi*1.5*1.5 = 13.03 is the flow rate, in some unknown units involving metres, inches, pounds etc.
The tank's volume is pi*(3/2)<sup>2</sup>*5 = 35.35m<sup>3</sup>
So the tank fills in about 2.71 hours, based on some unknown poundy inchy cuby metre-like unit times hour<sup>-1<sup>
[Edited on 5-3-2016 by aga] |
I checked the consistence of the units, that got my grey matter working LOL. So with the velocity in m/s density in kg/m**3 the pressure is in
Newtons/m**2 . Yes the conversions are yucky especially with bars thrown in.
Ref: N/m**2 - kg/m**3. x (m/s)**2
Simplifying the right side results in kg/(m x s**2)
Multiplying both sides by m**2 results in N equals kg.m/s**2
Which is correct QED
[Edited on 5-3-2016 by wg48]
|
|
|
Fulmen
International Hazard
    
Posts: 1725
Registered: 24-9-2005
Member Is Offline
Mood: Bored
|
|
You're right, I've just never dealt with idealized problems before. I've calculated many similar problems, but always with some pump specifications
(and with pipe losses to calculate). Bernoulli's should give the answer to the flow rate out of the pipe.
We're not banging rocks together here. We know how to put a man back together.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by wg48  | | I checked the consistence of the units, that got my grey matter working LOL. So with the velocity in m/s density in kg/m**3 the pressure is in
Newtons/m**2 . Yes the conversions are yucky especially with bars thrown in. |
Not sure what you mean wg48.
Glad your brain cells were mobilised, so what are the units ?
I certainly don't know.
[Edited on 5-3-2016 by aga]
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | Quote: Originally posted by wg48  | | I checked the consistence of the units, that got my grey matter working LOL. So with the velocity in m/s density in kg/m**3 the pressure is in
Newtons/m**2 . Yes the conversions are yucky especially with bars thrown in. |
Not sure what you mean wg48.
Glad your brain cells we mobilised, so what are the units ?
I certainly don't know. |
See my addendum
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
what does ** mean ?
|
|
|
wg48
National Hazard
   
Posts: 821
Registered: 21-11-2015
Member Is Offline
Mood: No Mood
|
|
Raised to the power of ie x**2 is x squared, x**3 is x cubed
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
x^3 would be more understandable.
Thanks for the explanation.
Edit:
So what are the units ?
[Edited on 5-3-2016 by aga]
|
|
|
| Pages:
1
2
3 |