| Pages:
1
..
9
10
11
12
13
..
33 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Hybridisation
The valence electrons of the elements Be through to C often undergo so-called hybridisation.
Hybridisation helps explain bond structure and molecular shape.
Take the example of Boron, [He]2s<sup>2</sup> 2p<sup>1</sup>. Hybridisation causes a new type of atomic orbital (AO) to form,
termed sp<sup>2</sup>. There are three sp<sup>2</sup> orbitals, each contain 1 unpaired electron and all three orbitals are at
the same energy level.
Spatially, they are arranged like this:
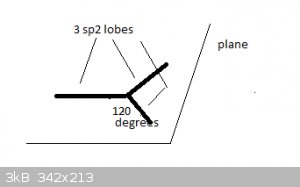
The three sp<sup>2</sup> orbitals much resemble the 'half lobes' of a p<sub>x</sub> orbital and are represented here by thick
lines. The orbitals lie in a single plane and at 120 degree angles of each other.
They form sigma bonds with s or p<sub>x</sub> atomic orbitals, like p<sub>x</sub> orbitals do.
sp<sup>2</sup> hybrid orbitals and the bonding MOs they form explain why B forms planar, triangular molecules like
BH<sub>3</sub> and BCl<sub>3</sub>.
sp<sup>2</sup> hybridisation also explains the shape of molecules like CH<sub>2</sub>=CH<sub>2</sub>.
The Ground State for carbon is 2s<sup>2</sup> 2p<sup>2</sup>. As sp<sup>2</sup> hybridisation causes one of the 2s
to jump to the 2p orbital, and 3 of the 4 electrons then form half-occupied sp<sup>2</sup> orbitals but the p<sub>z</sub>
orbital remains unaffected (and half-occupied). The 3 sp<sup>2</sup> orbitals lie in the plane and are represented here by thick black
lines, the remaining p<sub>z</sub> orbital is in green and is vertical to the plane:
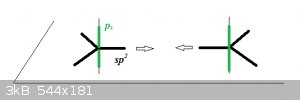
When the atoms approach, the sp<sup>2</sup> orbitals form a σ MO and the pz orbitals a π MO. The remaining 4 sp<sup>2</sup>
orbitals bond with 1s<sup>1</sup> hydrogen AOs.
sp<sup>3</sup> hybridisation: 4 unpaired electrons each in one in four iso-energetic orbitals. Spatially they arrange as
a tetrahedron with the nucleus at the centre and the lobes pointing to the corners of the tetrahedron. Explains the tetrahedral structure of
CH<sub>4</sub>, CX<sub>4</sub> (carbon halides) and the shape of alkanes in general.
Hybridisation can be interpreted as the need to minimise the electrostatic repulsion between MOs. In each case (sp, sp2 and sp3) the angles between
the resulting MOs is such that electrostatic repulsion between them is minimal (but not zero).
NH<sub>3</sub> is another example. Nitrogen's valence electrons 2s<sup>2</sup> 2p<sup>3</sup> also undergo an sp3
hybridisation, albeit with a small difference. One of the sp<sup>3</sup> orbitals contains a full pair of electrons (paired up and down),
the three others each one unpaired electron (three half-filled sp<sup>3</sup> orbitals).
The latter three orbitals combine with 3 hydrogen 1s1 atomic orbitals to form NH<sub>3</sub> by means of sigma bonds.
The result is a tetrahydron with three N-H sigma bonds pointing 'downwards' and one lone electron pair pointing 'upwards'.
The lone electron pair that is left after hydrogen bnding explains why ammonium ions (NH<sub>4</sub><sup>+</sup> exist: with a proton (H+, no electrons) the lone electron pair of NH3 can form a
bonding sigma orbital. NH<sub>4</sub><sup>+</sup> is also a tetrahydron. All four N-H sigma bonds in
NH>sub>4</sub><sup>+</sup> are identical in all respects. exist: with a proton (H+, no electrons) the lone electron pair of NH3 can form a
bonding sigma orbital. NH<sub>4</sub><sup>+</sup> is also a tetrahydron. All four N-H sigma bonds in
NH>sub>4</sub><sup>+</sup> are identical in all respects.
Water and the oxonium ion
In the preceding section I told a little white lie. The structure and shape of the H2O molecule can also explained by means of sp3 hybridisation of
the 2s2 2p4 valence electrons of oxygen. Two of the four tetrahydrally oriented sp3 orbitals are fully filled (2 opposing spin electrons), two contain
a lone electron. The latter two form sigma bonds with the 1s1 electrons of two hydrogen atoms. And as explained above, the high electrostatic
repulsion between the two unbonded sp3 orbitals then forces the H-O bond angle to 104.5 degrees.
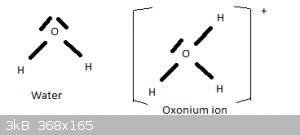
If one of the full sp3 orbitals forms a sigma bond with a proton (H+), this is the oxonium (aka hydronium) ion H3O+.
Special mini-interlude for aga:
Because I know he’s been dying to see some chemical reaction explained by QM/WM, here we have our first simple example: the auto-dissociation of
water:
H<sub>2</sub>O(aq) + H<sub>2</sub>O(aq) < === > H<sub>3</sub>O<sup>+</sup>(aq) +
OH<sup>-</sup>(aq)
This (much left leaning) equilibrium is made possible by one of these full but unbonded sp3 orbitals ‘donating’ its electrons to a proton and
forming a covalent σ, identical to the two other H-O bonds in water.
[Edited on 23-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The hybridised thing troubles my addled mind, but not so much as the Equilibrium.
What powers the constant to-and-fro of elemental/hydronium ion formations ?
If we assume that electrons are always in motion, then that is a clue i suppose.
Why does hybridisation happen ?
Would an opposing pair of electrons simply prefer their own room ?
(i would: i hate sharing my room with an opposing electron).
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Oooopppssieie: massive typo alert (already fixed), that reaction should have been (OF COURSE):
2 H<sub>2</sub>O(aq) < === > H<sub>3</sub>O<sup>+</sup>(aq) + OH<sup>-</sup>(aq)
The equilibrium constant for this reaction is:
K<sub>w</sub> = [H<sub>3</sub>O<sup>+</sup>] x [OH<sup>-</sup>] = 10<sup>-14</sup>
Hybridisation happens because it provides outcomes of minimum inter-MO electrostatic repulsion, therefore minimum potential energy (stored in the
molecule as electrostatic potential).
[Edited on 22-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
One did not wish to trouble one with such simplicities, seeing as the subject matter is of far greater import.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | | One did not wish to trouble one with such simplicities, seeing as the subject matter is of far greater import. |
You say that but this could have been the biggest SM bloopers/outtakes since Fry and Laurie!
https://www.youtube.com/watch?v=2un9rO2ZF4g
Blooper free: without hybridisation, the shapes for BH3, CH4, H2O and NH3 would predict 90 degrees angles between the E-H bonds.
[Edited on 22-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Why does Hybridisation happen ?
Is it simply that electrons prefer to NOT share an orbital ?
Edit:
Your edit already explained Why.
Sorry.
[Edited on 24-9-2015 by aga]
|
|
|
Metacelsus
International Hazard
    
Posts: 2539
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
I've been reading more about quantum mechanics and wavefunctions. Could someone explain to me what a Hamiltonian is, and how to use one? (I know it's
something related to the total energy of the system, but how does it relate to the Schrödinger equation?)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Let's look at the Schrödinger equation in one dimension:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/scheq.htm...
(try and keep this window open)
It's a second order differential equation and now look at the different terms, from left to right:
a) First term:
-(ћ<sup>2</sup>/2m) δ<sup>2</sup>ψ(x)/δx<sup>2</sup>
(With ћ = h/(2π) (“h bar”))
It tells you to take the second derivative of the system's wave function ψ(x) and multiply the result with -(ћ<sup>2</sup>/2m).
b) Second term:
U(x)ψ(x) with U(x) the potential energy function.
So this term means 'multiply the wave function with the potential energy function of the system'.
We often combine the first and second term using operator algebra:
[-(ћ<sup>2</sup>/2m)δ<sup>2</sup>/δx<sup>2</sup>+U(x)]ψ(x) = Hψ(x), where
H is the Hamiltonian Operator, which acts on the wave function ψ(x).
c) Third term, right to the equal sign:
Eψ(x) where E is the total energy of the system.
This term means 'multiply the total energy of the system with the wave function'.
Put it all together and the SE means:
'The Hamiltonian Operator H acting on the wave function ψ(x) yields the product of the total energy of the system E
and the wave function ψ(x)'.
In mathematical formulation you get one of the most famous equations in physics:
Hψ=Eψ
[Edited on 25-9-2015 by blogfast25]
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Cheddite Cheese  | | I've been reading more about quantum mechanics and wavefunctions. Could someone explain to me what a Hamiltonian is, and how to use one? (I know it's
something related to the total energy of the system, but how does it relate to the Schrödinger equation?) |
In quantum mechanics observables are associated with operators that act on wave functions. So anything you observe, the position of an electron, its
energy, the angular momentum of a molecule, the spin of a nucleus, the momentum of an atom, the electric or magnetic field at a point of space---there
is an operator corresponding to each of these.
In classical mechanics an observable is just a function of the dynamical state of the system. For example, the kinetic energy of a particle is (1/2)
mv^2. The "dynamical state of the system" means its position and velocity, and the kinetic energy is a function of the velocity. The total energy is
the kinetic energy plus the potential energy, V(x), which depends on the position x. So the total energy is a function of the position and velocity
of the particle, that is, of its dynamical state. Similarly, the z-component of angular momentum is m(xv_y - yv_x), another function of the dynamical
state. The linear momentum is mv.
In quantum mechanics the operator corresponding to the position of the particle is multiplication by x, that is, the x operator converts the wave
function psi(x) into x psi(x), a new wave function. The operator corresponding to momentum (in one dimension) is -i hbar d/dx, a differential
operator. When momentum acts on psi(x), it produces -i hbar d psi(x)/dx.
These rules for associating these two observables (position and momentum) with operators are not supposed to be obvious. They were worked out over a
period of twenty years or so during the development of quantum mechanics.
But once these rules for position and momentum are known, then the operators corresponding to other observables become known. For this purpose it is
convenient to express the classical observable as a function of position and momentum, rather than position and velocity. The conversion is easy,
because p=mv. For example, the classical energy, expressed as a function of position and momentum, is
E = p^2/2m + V(x)
To get the corresponding operator in quantum mechanics, we just replace the classical x and p by their operators, x -> multiplication by x, p ->
-i hbar d/dx. So, the energy operator, what is usually called the Hamiltonian and written H instead of E, becomes
H= - (1/2m) hbar^2 d^2/dx^2 + V(x)
It is a second order differential operator.
In classical mechanics there is a sense in which the energy is the "generator" of time evolution, that is, the small correction to the dynamical state
of a system after a small time dt can be expressed in terms of the energy. This idea carries over to quantum mechanics. If psi(x,t) is the wave
function at time t, then the change in psi when t goes from t to t+dt is
psi(x,t+dt) - psi(x,t) = - dt (i/hbar) H psi(x,t)
where H is the Hamiltonian operator. Dividing this by dt, you get a differential equation in time,
i hbar partial psi(x,t)/partial t = H psi(x,t).
This is the Schro"dinger equation.
This is explained more carefully in my notes,
http://bohr.physics.berkeley.edu/classes/221/1112/notes/tevo...
These notes are for a second (graduate) course in QM, not an introductory course, so they are more advanced than you would find in an introductory
book. However, I was at some pains to explain the subject carefully, so you may find them useful.
[Edited on 25-9-2015 by annaandherdad]
[Edited on 25-9-2015 by annaandherdad]
Any other SF Bay chemists?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
A reminder for any 'Johnnie-come-latelys':
Table of content of Part I
|
|
|
Metacelsus
International Hazard
    
Posts: 2539
Registered: 26-12-2012
Location: Boston, MA
Member Is Offline
Mood: Double, double, toil and trouble
|
|
So, basically the Hamiltonian is an operator on the wavefunction, and its eigenstates represent allowed energy levels. I think I get it now.
Also, I just learned that whether or not operators commute is representative of whether or not observable quantities have an uncertainty relation.
Quite interesting!
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Cheddite Cheese  | So, basically the Hamiltonian is an operator on the wavefunction, and its eigenstates represent allowed energy levels. I think I get it now.
Also, I just learned that whether or not operators commute is representative of whether or not observable quantities have an uncertainty relation.
Quite interesting! |
Yes, H is the Total Energy operator.
Other operators.
Oh, and it appears AAHD and me wrote our responses at almost exactly the same time. Her's is for the time dependent SE, mine's for the time
independent SE.
For time independent eigenfunctions ψ(x) of the TISE with total energy E, you can find the time dependent equation as:
ψ(x,t) = ψ(x)e<sup>-iEt/ћ</sup> and at t = 0, ψ(x,0) = ψ(x). But it's only valid for eigenstates ψ(x), E.
[Edited on 25-9-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Higher Hybridisations
Let’s look at the structure and bonding of the well known aluminium hexaqua cation
[Al(H<sub>2</sub>O)<sub>6</sub>]<sup>3+</sup>.
The 'naked ' Al<sup>3+</sup> ion has lost its valence electrons 3s2 3p1, so its level 3 orbitals are now empty.
The empty 3s orbital, three empty 3p suborbitals and two empty 3d suborbitals hybridise into six sp3d2 orbitals, all empty.
Each water molecule now donates one of its lone electron pairs (filled orbitals) to these empty hybrid atomic orbitals, resulting in the following
structure.
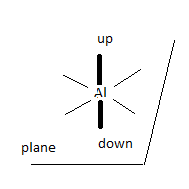
Four of the bonds (represented by thin lines, water molecules not shown) lie in a plane, one points perpendicularly 'upwards', one perpendicularly
'downwards' (both represented by thick lines, water molecules not shown).
An ‘artist’s impression’ of a full sp3 water MO approaching an empty z-oriented sp3d2:
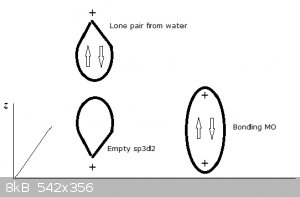
This kind of bonding is also referred to as dative and electron pair donors like water, ammonia and many others as Lewis bases. Conversely
Al<sup>3+</sup> is a Lewis acid (electron pair receptor). The principle of dative bonding explains the structure of many hydrated
cations.
A partial explanation of the colours of transition cation complexes
As an example we'll use the strongly blue coloured hydrated titanous(III)
[Ti(H<sub>2</sub>O)<sub>6</sub>]<sup>3+</sup> cation. The blue colour indicates that the green component of white
light has been absorbed.
Titanium's electron configuration is [Ar]3d2 4s2 and the naked Ti3+ ion has lost one 3d and two 4s electrons, leaving it with [Ar]3d1.
The next orbitals are 4p, 5s and 4d orbitals which hybridise to six sp3d2 and these empty hybrid atomic orbitals accept one of the lone electron pairs
of each H2O molecule, resulting in an octagonal structure similar to that of the
[Al(H<sub>2</sub>O)<sub>6</sub>]<sup>3+</sup> ion.
The 5 suborbitals of the unfilled 3d orbital, like the px, py and pz suborbitals of any p orbital, are in principle degenerated because they all have
the same energy level.
The five d suborbitals are categorised into two subgroups: e and t.
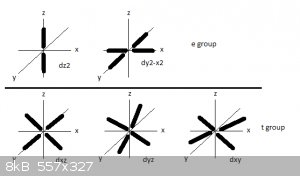
A reminder of the shapes and orientations of the 3d suborbitals, here:
http://winter.group.shef.ac.uk/orbitron/AOs/3d/index.html
In the first figure orbital lobes are represented by very thick lines. The e group contains the d<sub>z2</sub> and
d<sub>x2-y2</sub> suborbitals that have strong electron densities along the x, y and z axis.
The t group contains the d<sub>xy</sub>, d<sub>yz</sub> and d<sub>xz</sub> suborbitals that have strong electron
densities in the xy, yz and xz planes but not along the x, y and z axis.
The presence of filled sp3d2 hybrids in the hydrated cation causes an energy difference to occur between the e and t group 3d suborbitals because of
the difference in electron repulsion experienced between the sp3d2 orbitals and the e and t group suborbitals. The e suborbitals experience greater
electron repulsion by the sp3d2 filled hybrids than the t suborbitals.
This small energy difference causes the lone 3d1 electron to be able to absorb energy (E<sub>photon</sub> = hf) from visible light photons
(here, in the green part of the VIS spectrum) and 'toggle' between the higher and lower energy states of the e and t group suborbitals.
This general principle also applies to many other transition metal complexes with ligands like H<sub>2</sub>O, NH<sub>3</sub>,
Cl<sup>-</sup> and many others.
[Edited on 26-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by blogfast25  | bonding of the well known aluminium hexaqua cation [Al(H<sub>2</sub>O)<sub>6</sub>]<sup>3+</sup>.
The 'naked ' Al<sup>3+</sup> ion has lost its valence electrons 3s2 3p1, so its level 3 orbitals are now empty.
The empty 3s orbital, three empty 3p suborbitals and two empty 3d suborbitals hybridise into six sp3d2 orbitals, all empty.
|
How can an electron orbital be empty ?
With no electron, surely there is zero probability of finding one there.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
How can an electron orbital be empty ?
With no electron, surely there is zero probability of finding one there. |
Ah, a question after my own heart: on existence/non-existence, mathematical objects, the 'Real' and the meaning of life! 
Consider the transition from the ground state of carbon to its first excitation:
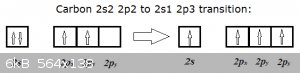
2s2 2p2 is carbon's ground state and 2s1 2p3 the first excitation (that explains C's tetravalence).
In the ground state, one of the three 2p orbitals is empty. So does this empty orbital really exist? Well, when the transition occurs, a 2s2 electron
'jumps' into the empty 2p<sub>z</sub> orbital... Or has that now half-filled 2p<sub>z</sub><sup>1</sup> been
'poofed' into existence, just for the occasion?
IMHO it matters not one iota: orbitals are mathematical objects that exist as descriptions of a Quantum state, whether they contain electrons or not.
So perhaps the empty Al<sup>3+</sup> sp<sup>3</sup>d<sup>2</sup> hybrid orbitals exist or maybe they jump into
existence when the dative lone electron pairs from water approaches them? I see no useful distinction here.
| Quote: | | With no electron, surely there is zero probability of finding one there. |
That's a weak argument: even in electron filled orbitals there are poinst where electron probability: the areas between the lobes, known as nodes:
http://winter.group.shef.ac.uk/orbitron/AOs/2p/index.html
[Edited on 30-9-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Electronegativity:
Electronegativity, χ<sup>P</sup>, was defined by Pauling as ‘the power of an atom in a molecule to attract electrons to itself’.
I won’t go into the quantitative definition of electronegativity because although Pauling’s version can be measured, it’s not an ‘objective’
measurement like ‘velocity’ or ‘mass’.
Below are the Pauling electronegativity values of some important elements, the higher the number the higher the power of an atom in a molecule to
attract electrons to itself:
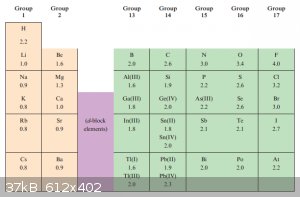
Although ‘electropositivity’ is an antonym of electronegativity, no value can be assigned to ‘electropositivity’. It’s therefore better to
state:
‘Element E1 is less electronegative than element E2’ than to state ‘Element E1 is more electropositive than element E2’.
Polar diatomic molecules:
Consider the structure of a simple diatomic molecule like HBr (hydrogen bromide):
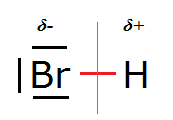
In it the Br nucleus is surrounded by three lone (non-bonding) electon pairs (orbitals) and one σ bonding molecular orbital (shown in red) which it
shares with the H nucleus.
However, the Pauling electronegativity values of Br and H are 3.0 and 2.2 respectively, so Br is more electronegative than H and attracts these σ
electrons more than does H. Quantum mechanically this means that the σ electron density (probability) will be higher on the left hand side of the
(green) line of symmetry than on the right hand side.
This causes the Br to be partially negatively charged, indicated by δ-, and the H atom to be partially positively charged, indicated by δ+. By δ
here should be understood 0 < δ < 1 (with respect to the unitary charge).
HBr is a permanent electrical dipole.
[Edited on 3-10-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
| Quote: | | That's a weak argument |
Ooops. After another Can i see that it is a pointless (!) argument.
Given what's been explained so far, a 0 probability is just as valid as a 1 probability as it isn't a Static system in any way, shape or form.
The 0 probabilities just define a rough limit to the extent of an orbital.
Electronegativity :
This implies that the effective positive charge on a Proton is greater than the negative charge on an Electron, by some small amount.
(maybe the distance from the protons in the nucleus modulates the relative charge effect of electrons in different orbitals)
Does it follow that within a column of the periodic table that the more Protons an atom has then the more electronegative it is ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: |
Electronegativity :
This implies that the effective positive charge on a Proton is greater than the negative charge on an Electron, by some small amount.
(maybe the distance from the protons in the nucleus modulates the relative charge effect of electrons in different orbitals)
Does it follow that within a column of the periodic table that the more Protons an atom has then the more electronegative it is ?
|
The charge of a proton and an electron are exactly the same (opposite in sign, of course).
The two electrons in the σ bonding orbital (represented by the red thickish line) spend on average more time left of the line of symmetry
(the Br side of the molecule) than right of the line of symmetry (the H side of the molecule). That makes the left side partially negatively charged
and the right side partially positively charged.
| Quote: | | Does it follow that within a column of the periodic table that the more Protons an atom has then the more electronegative it is ?
|
Look at the table and the values for χ of the halogens. Does that bear out your assertion? No.
It's more complicated than that but you're actually fairly close. Electronegative elements tend to be those whose outer atomic orbitals (valence
electrons) tend to be close to the nucleus. These and bonded electrons then tend to feel the pull of the nucleus more strongly (electrostatic
attraction being inversely proportional to electron/nucleus distance, squared).
Another important factor is shielding: the inner electrons (non-valence) tend to shield the outer ones from the nuclear electrostatic
attraction. That explains why the alkali metals are low on the electronegativity scale.
χ is really hard to predict on purely theoretical grounds, so the tabled values are ALL empirical.
[Edited on 3-10-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Huh ? Pauling Measured them ?!?!
There's a lot to think about here.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Well, I'm sure he had a lot of help doing that!    But he's
one of the fathers of the concept. But he's
one of the fathers of the concept.
[Edited on 3-10-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Polar and non-polar molecules:
We saw with the example of H-Br a molecule that has a net electrical dipole, due to bond polarisation as a result of differing values of χP of H and
Br. Such a molecule aligns itself in an electrical field with the negative side facing the anode and the positive side facing the cathode.
Since as most elements have different values for χP, bond polarisation is common. Now look at the following case of CF<sub>4</sub>:
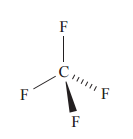
The difference in χP between C and F is about 1.4 and the C-F bonds are significantly polarised. But despite this, CF<sub>4</sub> is not
a polar (dipole) molecule and it doesn’t orient itself permanently in an electrical field. The four polarised bonds can be thought of as charge
vectors all pointing in the same direction with the same magnitude and cancelling each other out.
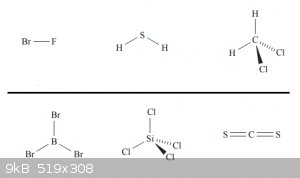
Below are some examples of polar and non-polar molecules, above the line are the polar ones, below the non polar ones:
[Edited on 4-10-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by blogfast25  | | Quote: | | Does it follow that within a column of the periodic table that the more Protons an atom has then the more electronegative it is ?
|
Look at the table and the values for χ of the halogens. Does that bear out your assertion? No.
It's more complicated than that but you're actually fairly close. Electronegative elements tend to be those whose outer atomic orbitals (valence
electrons) tend to be close to the nucleus. These and bonded electrons then tend to feel the pull of the nucleus more strongly (electrostatic
attraction being inversely proportional to electron/nucleus distance, squared).
Another important factor is shielding: the inner electrons (non-valence) tend to shield the outer ones from the nuclear electrostatic
attraction. That explains why the alkali metals are low on the electronegativity scale. |
While we're on the topic of electronegativity and its relationship to atomic size and number of protons, I suppose it might be a good time to also
point out the effect that atomic size has on charge strength/charge density of ions. For example, just like how fluorine is more electronegative than
iodine because it is smaller in size with fewer electrons between its outer electrons and inner non-bonding electrons, the negative charge on a
fluoride ion is also stronger than the negative charge on an iodide ion.
So while fluoride and iodide may both have the same overall charge of negative one, that charge is distributed over a much smaller area in fluoride
than it is in the much larger iodide. Because of this, despite both ions having the same formal charge of negative one, the negative charge on
fluoride is much, much, much stronger than it is on iodide. This same concept also applies to positive charges as well, for example the positive
charge on a tiny lithium ion being much stronger than the positive charge on a giant cesium ion.
This explains why the bond strength of LiF is the strongest of the alkali-halide salts, and the bond strength of CsI the weakest. Also, this concept
will later help you understand why the larger halides like bromide and iodide make better nucleophiles than the smaller ones like fluoride and
chloride, as well as why carbon-fluorine bonds are so strong and carbon-iodine bonds are so weak.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
@Darkstar:
Good addition, thank you.
High central electrical field strength of small, multivalent cations like Al<sup>3+</sup> and Fe<sup>3+</sup> (list not
exhaustive) also explains their ability to expel protons from their water mantle (for the solvated ions). i.e. undergo hydrolysis.
[Edited on 4-10-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by Darkstar  |
Another important factor is shielding: ...
... fluoride and iodide may both have the same overall charge of negative one, that charge is distributed over a much smaller area in fluoride than it
is in the much larger iodide... |
So the atoms really do have an 'effective' charge (as seen from the angle at which bonding takes place) that is not actually 1, although overall,
mathematically, taking the system as a whole, it is 1.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
aga:
I'll let Darkstar answer that one.
Good news, though: 2 more instalments till X-mas, I mean end of course. Then THE EXAM! So start cramming now!
|
|
|
| Pages:
1
..
9
10
11
12
13
..
33 |