| Pages:
1
..
7
8
9
10
11
..
33 |
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
1. So the Orbital is a plot of the probability of finding an electron at, say n=1 given a number of variables, such as What ? When ?
2. If so, then the isosurface is an imagined nice smooth surface, imagining a convenient boundary so it can be all nice and shiny for
the graphical representation, whereas the reality is a fuzzy blob occupying approximately that shape.
3.A bit like a line drawing of a cat, omitting the furry bits. |
2. and 3. are correct.
1. is imprecise.
ψ<sup>2</sup> is not "probability of finding an electron at", it's the probability density. To find the probability of the electron you
need to calculate it, using ψ<sup>2</sup> and a small volume element around the location you're interested in. Obviously, areas of high
ψ<sup>2</sup> tend to be areas where the probability of finding the electron is high. The 'lobes' of the orbitals are such areas. The
only variable here is r and the angles theta and phi, the position with respect to the nucleus. Remember, we're using spherical
coordinates here!
[Edited on 1-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Proability Density is a bit hard for my brain.
Also the Toroidal formations of some orbitals cause brain-pain.
Please explain.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga | Proability Density is a bit hard for my brain.
Also the Toroidal formations of some orbitals cause brain-pain.
Please explain. |
The toroidal formations cause everyone brain-pain! Look at the equation of the angular wave function Y for the
3d<sub>z2</sub> orbital (that's one of those with a torus):
http://winter.group.shef.ac.uk/orbitron/AOs/3d/equations.htm...
Don't lose your mind over it! 
And I'll let you off on the probability thingy: just look at ψ<sup>2</sup> (at a given location) as proportional to the
probability of finding the electron at that location. In areas of high ψ<sup>2</sup> you're more likely to find the electron.
[Edited on 2-9-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Multi-electronic elements: Helium and beyond
So far we’ve only dealt with the simplest of all atoms, hydrogen, which contains only one electron. Helium, the next one up in the Periodic Table,
contains two electrons.
We’ve seen that obtaining the eigenstates (wave functions and energy levels) can be obtained by solving the Schrӧdinger equation:
HΨ=EΨ
Where H is the Hamiltonian operator of the atom (the “total energy” operator, if you will).
An expression for the Helium Hamiltonian can be found here (Eq.9.2 to 9.5):
http://chemwiki.ucdavis.edu/Physical_Chemistry/Quantum_Mecha...
Where V(r<sub>1</sub> and V(r<sub>2</sub> represent the potential energies caused by the electrostatic
attractions between the nucleus and electron 1 and 2.
But note that there’s now an additional term V(r<sub>12</sub> which
represents the potential energy caused by mutual electrostatic repulsion between both electrons 1 and 2. (Note: I believe
the term V(r<sub>12</sub> should carry a positive sign, and not a
negative on as on that page, because it is a repulsion. But the sign matters little for our purposes here).
For atoms with three electrons more potential energy terms need to be added, see Eq.9.7 for the general case with i electrons.
The main problem is that even for the case of helium the resulting Schrӧdinger equation is no longer analytically solvable. No finite steps algorithm
exists to find general expressions for Ψ and E (the eigenstates).
The He SE can be solved only numerically with so-called iteration algorithms (to great precision) but numerical methods do not yield
algebraic expressions for Ψ and E like the ones we obtained for the Pi1DB, the Quantum Harmonic Oscillator and the Hydrogen atom.
In order to solve the problem of electron occupation in multi-electron atoms physicists have resorted to developing a number of rules, often
heuristically, sometimes empirically, sometimes formally, that help determine the electron configuration of atoms from He to beyond.
As an end to this installment I’ll introduce one of the most important of these rules:
The Pauli Exclusion Principle (PEP):
| Quote: | | It is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers (n, ℓ, m<sub>ℓ</sub>
and m<sub>s</sub>. |
Let’s read this kind of in reverse: it indicates that if 2 electrons share three quantum numbers, e.g. n = 1, l = 0, m<sub>l</sub> = 0,
then as long as those two electrons have different quantum spin numbers m<sub>s</sub> then that’s okay? Yes!
Note that n = 1, l = 0, m<sub>l</sub> = 0 is the Ground State of Hydrogen, aka 1s, and that m<sub>s</sub> can only take on two
values: + ½ or – ½.
So the PEP is telling us that the 1s orbital can accommodate 2 electrons, as long as they have different quantum spin numbers.
The ground state of Hydrogen is represented by 1s<sup>1</sup>, the ground state of Helium by 1s<sup>2</sup>. Because electron
spin is often represented by an upward or downward arrow, these ground states are often depicted as:
The box symbolizes the 1s orbital, the arrows the electrons and their quantum spins. Note that for 1s<sup>1</sup> the arrow could also be
pointing down, without violating anything.
But there are more ramifications for electron configurations flowing from the PEP. For instance, could we cram another electron into
1s<sup>2</sup>? The answer is no: the third electron would inevitably share its quantum spin number with either of the two others, thereby
violating the PEP.
In short, 1s<sup>2</sup> is fine but 1s<sup>3</sup> is forbidden, verboten, haram, kaput. We’ll later see
that this principle of electrons in atomic orbitals of forming doublets is general and which other rules are needed to explain the electron
configurations of multi-electron atoms and even explain the Periodic Table itself!
[Edited on 3-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Too late - i looked.
OK, i've come to terms with the fact that i cannot follow the maths, however your clear explanations of what they mean are easy to
follow.
Does that mean that the algebra doesn't work out properly, so the equations have to be tried with real values over and over again to see what comes
out ?
Can i safely assume that basically says that two particles cannot occupy the same space at the same time (they would not fit) ?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
An example of an iteration method for finding the roots of a function f(x), if calculus fails:
https://en.wikipedia.org/wiki/Secant_method#The_method
By repeating the process the iteration values x<sub>1</sub>, x<sub>2</sub>, x<sub>3</sub>,
...,x<sub>i</sub>, converge to a stable, 'true' value of x (the sought root). Of course the SE is a differential equation and
requires a specific iteration approach but the philosophy is the same.
| Quote: | | Can i safely assume that basically says that two particles cannot occupy the same space at the same time (they would not fit) ?
|
Specifically, no 2 electrons can occupy the same state (here: orbital) if they have the same values for their four quantum numbers.
But take an orbital with n = 2, l = 1 and m<sub>l</sub> = 0, which is a p-suborbital. It can contain 2 electrons, provided one is spin up
and one is spin down. That way both electrons occupy the same state, except for their quantum spin state.
[Edited on 2-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So, given that their properties are identical in that n = 2, l = 1 and ml = 0, they must be different in some other way, hence spin Up and spin Down,
introducing another property in which way they can be different.
Starting to sound kinda familar.
|
|
|
Darkstar
Hazard to Others
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
| Quote: Originally posted by aga | | Can i safely assume that basically says that two particles cannot occupy the same space at the same time (they would not fit) ?
|
They'll "fit" alright. With enough pressure, you can fit as many of them little bastards in the same space as you want. Under pressure, the first
particles to go will be the protons and electrons. These will fuse with one another to create a bunch of neutrons, which are far more resistant to
collapse. Now, in the event that the pressure is strong enough to overcome even the degeneracy pressure of those neutrons, they, too, will be forced
to occupy the same space. And after those neutrons go, there will be nothing left to prevent or resist further collapse.
This is how most black holes form, by the way.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Final instalment of Part I by the end of this week. Phew!
Darkstar, can you point to the page that contains that Table of Content you so kindly made? I'll update it myself here, before going to Part II.
Thanks!
aga: please note that Darkstar is correct but to observe the things he describe requires electron pressures many, many orders of magnitude higher than
what can be supplied by the electrostatic attraction between the nucleus and the atom's electrons.
[Edited on 3-9-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
| Quote: Originally posted by blogfast25 | | Darkstar, can you point to the page that contains that Table of Content you so kindly made? I'll update it myself here, before going to Part II.
Thanks! |
Here is the post. Be sure to read the part in red before you add to it, though. I initially copied the link to each post directly out of my
address bar only to end up having to redo them because they have a reference to the page the post is on. Since my posts per page is set to 50, the
page I see a post on may not always be the same page someone else sees it on.
Anyway, just make sure the links have "&goto=search&" between the topic ID and post ID and not "&page=some number." You can get the
correct link by simply right clicking on the "posted on..." link above the target post and selecting "copy link location" (or whatever it is for your
browser). So for example, the link to my table of contents post should look like this:
http://www.sciencemadness.org/talk/viewthread.php?tid=62973&...
and not this:
http://www.sciencemadness.org/talk/viewthread.php?tid=62973&...
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
| Quote: Originally posted by Darkstar | | They'll "fit" alright. With enough pressure, you can fit as many of them little bastards in the same space as you want. |
That doesn't make much intuitive sense.
It would suggest that all the 3-dimensional matter in a black hole was compressed into the same place at the same time, which clearly is mind
boggling.
Would that not be a case where the Pauli Exclusion Principle is violated ?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Not really. The PEP actually applies to a broader class of subatomic particles called fermions (to which electrons belong). But at the
pressure Darkstar is referring to electrons are squeezed into the protons, forming neutrons. Neutrons aren't fermions though, so they don't have to
obey the PEP...
[Edited on 3-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Electrons squashed into protons, now neutrons squashed into other neutrons ...
Is the core of a black hole actually a true singularity ?
Can this even be modelled by anything we have available, including QM ?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga |
Is the core of a black hole actually a true singularity ?
Can this even be modelled by anything we have available, including QM ? |
I'll only answer questions that I feel comfortable with answering and this is not one of these.
But in about an hour (or so) the final instalment of Part I will be published. 
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The Aufbau Principle:
As we’ve seen from the Pauli Exclusion Principle (PEP), a pair of electrons can occupy the same orbital or suborbital (same n, l and
m<sub>l</sub>, as long as the quantum spin numbers of both electrons
are different ([+1/2,-1/2] or [-1/2,+1/2]). So the ground state 1s<sup>2</sup> is allowed but 1s<sup>3</sup> violates the PEP.
So in the case of the third element Li, where does that third electron go? And what about the fourth for Be etc etc?
The so-called ‘Aufbau’ or filling of the atomic orbitals as more electrons are added to non-hydrogenic atoms is governed by a second rule, known
as the Madelung Energy Ordering Rule, often referred to as the diagonal rule:
https://en.wikipedia.org/wiki/Aufbau_principle#Madelung_ener...
Following this rule (follow the right arrows for the filling order), the third Li electron ends up occupying 2s, so Li’s electron configuration
becomes 1s<sup>2</sup>2s<sup>1</sup> and for Be we get 1s<sup>2</sup>2s<sup>2</sup> (where in
accordance with the PEP that fourth Be electron has different spin from that previous third one).
The electron configurations of Li and Be (ground states) thus can be represented as:
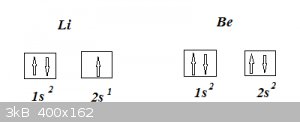
In our arsenal for successful ‘Aufbau’ we need one more element: Hund’s rule(s).
| Quote: | Hund's rule states that:
1. Every orbital in a sublevel is singly occupied before any orbital is doubly occupied.
2. All of the electrons in singly occupied orbitals have the same spin (to maximize total spin). |
The principle is well explained and illustrated here (but I'm not sure the link doesn't render properly here):
http://chemwiki.ucdavis.edu/Inorganic_Chemistry/Electronic_Configurations/Hund's_Rules
With the Pauli Exclusion Principle, the Diagonal Rule and Hund’s Rules we have the tools needed to predict the electron configurations of the
elements of the Periodic Table.
Example: Fe (Z = 26)
Electrons from 1<sup>st</sup> Period: 1s<sup>2</sup>
Electrons from 2<sup>nd</sup> Period: 2s<sup>2</sup> and 2p<sup>6</sup>
Electrons from 3<sup>rd</sup> Period: 3s<sup>2</sup> and 3p<sup>6</sup>
That’s 2 + 8 + 8 = 18 electrons so far.
Fourth period filling starts with 4s<sup>2</sup> but then, following the Diagonal rule continues by filling 3d, with the 6 remaining
electrons, so 3d<sup>6</sup>. The distribution of these 6 electrons over the five 4d-suborbitals is given by Hund’s rules:
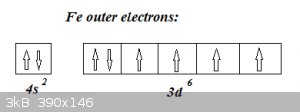
Obviously for high Z this can be a bit of a kerfuffle, so we can apply a shortcut. Take e.g. Te (Z = 52). Find the nearest Group 18 (Noble gases)
element with a Z < 52, that is Kr (Z = 36) which is a Period 4 element. The electron configuration of Te is then that of Kr, with the
added electrons to get to 52 electrons, so:
[Te] = [Kr]5s<sup>2</sup>4d<sup>10</sup>5p<sup>4</sup>
Importance of Outer electrons in Chemical Bonding
Getting near the end well of Part I this is probably a good place to remind readers that chemical bonds (the subject of Part II) only involve the
outermost electrons (the so-called valence electrons) because the inner electrons are far too tightly bound to the nucleus to get involved in
molecular orbitals (or ionic bonds).
A brief explanation of the Periodic Table of the Elements
When Dimitri Mendeleev in 1869 presented his version of the Periodic Table this ‘Eureka!’ moment was also accompanied by much wonderment as to
what really caused this arrangement to be correct. It was only with the advent of QM that the explanation was found to be the way atomic orbitals fill
up.
Using the modern representation of the Periodic Table, like here:
http://sciencenotes.org/printable-periodic-table/
... we can distinguish different areas, aka ‘blocks’ which are the direct consequence of atomic orbital filling (‘Aufbau’) in accordance with
the laws and rules of QM.
Groups 1 and 2 (formerly IA and IIA) as known as the s-block because the outer (valence) electrons of the atoms of the elements in that group are
assigned to s-orbitals.
Groups 13 through to 18 (formerly IIIA to VIIIA) are called the p-block because the outer valence orbital have been filled up with (three) p-orbitals.
Groups 3 through to 12 are called d-block elements. From Period 4 something interesting happens: when calcium’s outer orbital 4s is full
(4s<sup>2</sup> the diagonal rule tells us that the orbital filling now
continues at 3d (and not 4p as might otherwise be expected). There are five d-suborbitals, each accommodating 2 electrons, so the d-block is 10 groups
wide. The same effect repeats at periods 5,6 and 7 where orbital filling is respectively via 4d, 5d and 6d.
But in periods 6 and 7 something similar happens. For elements 57 to 71 (Lanthanides) orbital filling proceeds via 4f, for elements 89 to 103
(Actinides) orbital filling proceeds via 5f. There are seven f-suborbitals, each accommodating 2 electrons, so the f-block is 14 groups wide (together
the Lanthanides and Actinides are the f-block).
[Edited on 4-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Missed the closing square bracket on the starting url bit is all, and put an = in there instead.
How on earth did Mendeleev work out the PT ?
Presumably not QM ?
[Edited on 4-9-2015 by aga]
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by aga |
Missed the closing square bracket on the starting url bit is all, and put an = in there instead.
How on earth did Mendeleev work out the PT ?
Presumably not QM ?
|
Nope. Still doesn't render.
People had been working for a PT type arrangement for a long time with mixed results, as had Mendeleev. It kind of 'came to him', in a moment of
inspiration.
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quick Navigation (updated):
Part I – Basic Wave Mechanics
Additional Contributions
|
|
|
aga
Forum Drunkard
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
http://chemwiki.ucdavis.edu/Inorganic_Chemistry/Electronic_C...
That one gets close enough.
|
|
|
Little_Ghost_again
National Hazard
Posts: 985
Registered: 16-9-2014
Member Is Offline
Mood: Baffled
|
|
I am following but most of it is above my level! I am enjoying it alot though. I just thought I would make you aware I was lurking but trying not to
ask questions that made me sound stupid .
Dont ask me, I only know enough to be dangerous
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Thanks, L_G_A, I appreciate it!
|
|
|
Little_Ghost_again
National Hazard
Posts: 985
Registered: 16-9-2014
Member Is Offline
Mood: Baffled
|
|
I wont disturb this thread but I might have a question in a couple of days.
I have a old book on valence theory, so while following some of this thread I have also read some of the book. In places the book seems to be???
(wrong isnt the right word but close), I am wondering if its more a case that a pretty old book on this is now too out of date to be much use?
I cant formulate a decent question at the moment as I dont understand some of the maths (I am working on it), but as soon as I can identify what I
think the discrepancy is I will post the question.
I know its a science forum but a maths section would be cool! some of us dont have great maths but want to learn
Dont ask me, I only know enough to be dangerous
|
|
|
Darkstar
Hazard to Others
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
| Quote: Originally posted by Little_Ghost_again | I have a old book on valence theory, so while following some of this thread I have also read some of the book. In places the book seems to be???
(wrong isnt the right word but close), I am wondering if its more a case that a pretty old book on this is now too out of date to be much use?
|
What level is the book? I'm guessing it's more of a beginner-level book? It could just be that the explanations given here are just slightly more
advanced than what is written in the book, making the book's explanations seem almost wrong but not quite. This is a common issue in just
about all of the natural sciences, with physics being the most notorious of the bunch. Basically, many times the explanation you're given when first
introduced to a concept is seen as not really being correct from a more advanced level of view. To make matters worse, sometimes even the more
advanced level's view is also considered incorrect once you get even more advanced. It's kind of a pain in the ass, honestly.
For example, as I mentioned in an earlier post, you're initially taught that particles also behave like waves, and exhibit this sort of "wave-particle
duality" where they behave like both waves and particles at the same time. That's all fine and dandy when you're just starting out, as it helps you to
stop thinking about particles in the classical way that you're used to; however, once you start getting more advanced, you learn that the truth of the
matter is that, while a quantum object does sometimes behave like a wave and other times like a particle, the vast majority of the time it behaves
like neither. And when that particle does "behave like a wave," it isn't literally a real, physical wave that propagates through three-dimensional
space, but rather one that exists in an abstract mathematical space called Hilbert space. The problem, however, is that the latter explanation is not
exactly beginner-friendly.
A similar example in chemistry would be how acids are initially taught. At first, you're taught that things like HCl dissolve in water to give a bunch
of free protons in solution. It's only later that you learn it actually protonates the water molecules and produces a bunch of hydronium ions. And
even then, once you get slightly more advanced, you find out that there's still more to it. (Grotthuss mechanism)
To put it simply: you have to crawl before you walk!
|
|
|
annaandherdad
Hazard to Others
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
When I was a student I learned a lot from an old book by Pauling and Wilson, "Introduction to Quantum Mechanics with Applications to Chemistry" or
something like that. It's available as a Dover reprint pretty cheap. I thought it was really well written and easy to understand.
Darkstar---I wouldn't say that the waves are in Hilbert space, but you are right that they are not in real (3-dimensional) space. Rather, the waves
are in configuration space. For example, the wave function for the electrons in helium move in a six-dimensional space (configuration space) with
coordinates (x1,y1,z1,x2,y2,z2), the xyz coordinates of the two electrons.
Hilbert space is an abstract space in which a single point represents an entire wave function.
Also, it would be equally valid to say the wave lives in momentum space. See section 2 of my notes,
http://bohr.physics.berkeley.edu/classes/221/1112/notes/hilb...
Any other SF Bay chemists?
|
|
|
blogfast25
International Hazard
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
| Quote: Originally posted by Little_Ghost_again |
I have a old book on valence theory, so while following some of this thread I have also read some of the book. In places the book seems to be???
(wrong isnt the right word but close), I am wondering if its more a case that a pretty old book on this is now too out of date to be much use?
|
Text books (as opposed to peer reviewed papers) often place too much emphasis on valence theory to explain which compounds can exist and which not.
For a compound to be 'stable' (in itself a relative and subjective term) it's Change of Free Energy of Formation needs to be negative. Although
considerations of AO and MO definitely play a part in this, other factors like entropy changes and lattice energies do to.
That's why simple 'rules' like the Octet Rule often work but have many exceptions. Nature doesn't always comply to our sometimes reductionist
theories.
|
|
|
| Pages:
1
..
7
8
9
10
11
..
33 |
![[*]](images/xpblue/default_icon.gif){kind=icon}
