| Pages:
1
..
6
7
8
9
10
..
33 |
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
THE Hamiltonian operator (total energy of a quantum system) isn't too bad. Quantum operators in their full glory and properties... now that
IS serious stuff!
[Edited on 11-8-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
We’re nearing the last of Part 1, which mainly concerns itself with the QM of the Hydrogen atom. So I bring you another mathematical
(mini-)interlude, as well as the first part of the hydrogen atom’s treatment. Enjoy!
Another math mini-excursion: Cartesian and Spherical Coordinates
Because the hydrogen atom is roughly spherical the Schrodinger equation is ‘easier’ to solve when anchored in a spherical coordinate system than a
Cartesian one.
A Cartesian coordinate system is composed of three perpendicular axis X, Y and Z that intersect at the point of origin O. The position of any point in
space with respect to the Cartesian coordinate system is unequivocally determined by (x,y,z).
Now look a Spherical Coordinate System, here ‘superimposed’ on the Cartesian system:
https://en.wikipedia.org/wiki/Spherical_coordinate_system
The Spherical system uses r, θ and φ to define the point’s position in space:
1) Radial distance r is the distance between the point and the origin O (0,0,0).
2) Polar angle θ is the angle between the projection of the line that connects the point and O onto the XY plane and the X axis.
3) Azimuthal angle φ is the angle between the line that connects the point and O and the Z axis.
So the point’s position in space is now defined unequivocally by (r,θ,φ) (angles are expressed in Radian: 360 degrees is 2π)
The relationships between x, y, z and r, θ, φ are:
x = r sinθ cosφ
y = r sinθ sinφ
z = r cosθ
Using these relationships, any function F(x,y,z) can be transformed into a new function R(r,θ,φ).
And here’s a little teaser on just about how useful this can all be.
The Cartesian coordinate based equation for a sphere with radius R and centre point in O is:
R<sup>2</sup> = x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup>, quite a mouthful, huh?
And in spherical coordinates?
r = R, and that’s it!
You can prove this by plugging the relationships for x, y and z into the previous equation, if you’re that way inclined!
++++++++++++
The Hydrogen Atom’s Schrodinger Equation
In a mono-electronic atom the potential energy function of the electron is determined by the electrostatic attraction exerted by the positively
charged nucleus on the negatively charged electron. It depends only on the distance r between the electron and the nucleus:
U(r) = - e<sup>2</sup>/(4πε<sub>0</sub>r)
U(r) is a radially symmetrical function and ideal for treatment in spherical coordinates.
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydsch.ht...
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydsch.ht...
The transformation of coordinate system (Cartesian to Spherical), with some VERY nifty rearranging, splits the SE into three parts: the Radial
Equation, the Colatitude Equation and the Azimuthal Equation:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydsch.ht...
Quantum numbers
Similarly the hydrogen atom’s wave function itself is transformed into the product of three functions:
Ψ(x,y,x) === > Ψ(r,θ,φ) = R(r) P(θ) F(φ)
With each part (radial, colatitudinal, azimuthal) are associated Quantum Numbers:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydsch.ht...
R(r): the Principal Quantum Number n = 1, 2, 3, 4,…
P(θ): Orbital Quantum Number l = 0, 1, 2, … n - 1
F(φ): Magnetic Quantum Number m<sub>l</sub> = - l, - l + 1, to + l
In addition, electrons have an intrinsic (regardless of physical system they find themselves contained in) Spin Quantum Number,
m<sub>s</sub> = - ½ or + ½.
http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html#c1
[Edited on 14-8-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by blogfast25  | Darkstar:
Would you consider authoring a small segment on the Uncertainty Principle? Perhaps one that relates confinement energy to well size? As we know
confinement energy is more or less inversely proportional to well size. |
Sorry for the delayed response; it's been a busy last couple of weeks for me. I see you went ahead and introduced the uncertainty principle, so that's
good. I may write a brief segment later to specifically address some of the most common misconceptions about the uncertainty principle. For example,
the uncertainty having nothing to do with the measurement instrument itself, or how the uncertainty principle is not about single measurements and/or
single particles, but is instead a statistical statement about subsequent measurements of identically-prepared systems.
Of all the concepts in QM, it seems like HUP is the one students have the most trouble understanding. It is easily one of the most widely
misunderstood concepts in modern physics, and I think a lot of it is due to the way HUP is frequently taught at the undergraduate level, especially in
chemistry and other non-QM courses. I remember briefly covering the uncertainty principle back in General Chemistry I, only it was incorrectly taught
as something more akin to the observer effect. Instead of explaining the uncertainty when attempting to measure conjugate pairs simultaneously as
being an inherent property of matter due to the very nature of the physical universe itself, it was instead explained as though the uncertainty is due
to the actual act of measurement, which alters what is being observed by interacting with it.
And speaking of QM misconceptions, don't even get me started on the biggest one of them all: that wildly popular pre-QM myth known as wave-particle
duality--a non-existent concept that just won't die despite being outdated for nearly 100 years. The truth is that while quantum objects do sometimes
behave like waves and other times like particles, the vast majority of the time they behave like neither. And when a particle does "behave like a
wave," it isn't literally some real, physical wave that actually propagates through three-dimensional space, but rather one that propagates through an
abstract mathematical concept known as Hilbert space. There's a reason you rarely ever see "wave-particle duality" mentioned anywhere in advanced or
highly-technical QM books!
And, yes, the above part, while technically true, was mostly tongue-in-cheek and is intended to be taken with a grain of salt. 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Darkstar  |
And speaking of QM misconceptions, don't even get me started on the biggest one of them all: that wildly popular pre-QM myth known as wave-particle
duality--a non-existent concept that just won't die despite being outdated for nearly 100 years. The truth is that while quantum objects do sometimes
behave like waves and other times like particles, the vast majority of the time they behave like neither. And when a particle does "behave like a
wave," it isn't literally some real, physical wave that actually propagates through three-dimensional space, but rather one that propagates through an
abstract mathematical concept known as Hilbert space. There's a reason you rarely ever see "wave-particle duality" mentioned anywhere in advanced or
highly-technical QM books!
|
My impression, as a perennial (and very modest level) student of QM, is that the original de Broglie hypothesis is viewed in Diracian (Hilbert space)
QM as nothing more than a quaint, antiquated and poor analogy.
It appears that in the Complex space, Classical wave mechanics and Quantum wave mechanics share quite a bit of mathematics but that this is shown to
be almost no more than a ‘coincidence’, when one moves the treatment to matrix mathematics in the Hilbert space.
Re. QM in the Hilbert space I’m still very much of a dilettante, to be completely honest. Having been ‘brought up’ on a diet of matter waves
(electrons) I will find it hard to ‘let go’. Someone will have to detain me in the ‘Hilbert Re-education Boot Camp’, I think! It must be
infuriating for the Youngens to see the Olds still fiddle with their charming but somewhat obsolete ‘waves’.
It's kind of ironic that one of the heroes of QM, Erwin Schrödinger himself, was a great believer in these matter waves, or at least for some time.
I can’t really see Hilbert space mathematics taught in middle schools any time sun though, so very sharply abstract it is.
I guess we need to take a leaf out of Scott Aaronson's book!
What do you think?
[Edited on 18-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
The failure of all models to accurately represent reality is a thing that bothers me a lot, which is my main interest in understanding what is already
known.
Not doing so great in that so far, but am back on the homework waggon.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by Darkstar  | So here's the question: If the alpha particle is initially trapped inside the nucleus and forbidden to escape, similar to how the particle in
the box is trapped and forbidden to escape, how is it that the alpha particle is eventually able to overcome the strong force and leave the potential
well, all without ever actually having enough energy to escape the nucleus in any classical sense? In other words, how might quantum tunneling be used
to explain this?
Hint: Unlike the particle in the box, the potential well the alpha particle is trapped in has finite potential walls. Now recall
wave-particle duality and Heisenberg's uncertainty principle.
|
Best guess is that it leaps the containments walls, uncertainly.
To be honest, the Maths have already slipped beyond my grasp, so i'll go back to page 4 or 5 and start again.
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Can't say I blame you for having trouble letting go. I tend to think that it's actually quite helpful--almost necessary, even--to first understand QM
in terms of "matter waves" before seriously trying to make sense of some of the more modern interpretations. So while the original de Broglie
hypothesis may very well be an outdated concept as far as modern physics is concerned, I honestly can't imagine ever having learned QM without it.
At the end of the day, I try not to get too hung up on all the technicalities. I simply stick to what makes the most sense to me and just acknowledge
that it may not always be entirely correct.
Correct, although "leap" is probably not the best way to describe it. In quantum tunneling, the particle, for lack of a better word, goes
through the barrier not over it, something that is forbidden classically. It would be like a rolling ball somehow making it to the other side
of a hill despite not actually having enough energy to roll up and over it.
In the case of alpha decay, because there's a non-zero probability that the alpha particle will be found outside of the nucleus, given enough time, it
eventually will be. When that happens, if the alpha particle is sufficiently far enough away from the nucleus, the electromagnetic repulsion between
the two will become more significant than the attraction caused by the strong force, allowing the alpha particle to escape.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
My basic problem is that QM is internally inconsistent, in that the Assumptions are not really on-track, Conditions were Lifted to make it (the maths)
work and it's Popular amongst Mathematicians.
Granted : it's good for some things, however does not model Reality accurately.
Damn.
I said it and it's not really Over.
Classical and Quantum are not really at odds at all.
The fundamental problem is that they both offer a View of Reality in mathematical terms, and neither view is actually reality, as Reality is not bound
by our understanding of it.
[Edited on 22-8-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
aga:
I'm hesitating between a time-consuming, all-out, 'high brow' rebuttal of your last post and the futility of such a rebuttal. We seem to have gone
full circle as this is no more than a slightly more polite rehash of your prior statements re. QM (remember? The ones that prompted to organise this
series of basic 'lectures' to begin with?)
On balance I'll keep it short:
Quantum Mechanics as a theory does not rely on aga-like observers for its validity/invalidity. 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Going back to Darkstar's alpha emission problem, think particle in a box with finite potential wall (the potential V here is the Strong nuclear force
that keeps nuclei together, very simply put):
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pbox.html...
Such an alpha particle has limited (but NON-ZERO) probability density outside of the Classically allowed region (x=0, x=L), so that a detector can
(occasionally) pick it up outside of the nucleus (the potential well). It has 'tunnelled'.
[Edited on 22-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
That can't have been me !
Must have been HD using my password in order to tarnish my flawless professionalism and reputation as a clear thinker.
So the tunnelling phenonenon is that with non-infinite bounds, the particle can actually be 'seen' at some point beyond those bounds, albeit rarely.
Is that right ?
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by aga  | My basic problem is that QM is internally inconsistent, in that the Assumptions are not really on-track, Conditions were Lifted to make it (the maths)
work and it's Popular amongst Mathematicians.
Granted : it's good for some things, however does not model Reality accurately. |
I think you're seriously underestimating just how well QM does model reality. Just so it's clear, quantum mechanics is, bar none, THE most
accurate description of nature we have. Nothing else even comes close to modeling reality as accurately as QM/QFT does. Is it perfect? No. While
QM/QFT may accurately explain interactions between the strong force, weak force and electromagnetic force at the scale of atoms and subatomic
particles, it completely fails to explain gravity at distances that small.
So no, QM doesn't model reality 100% correctly, but it's pretty damn close. A theory that literally models reality perfectly would require unifying QM
(strong force, weak force and electromagnetism) and GR (gravity) to produce a Theory of Everything.
| Quote: |
Classical and Quantum are not really at odds at all.The fundamental problem is that they both offer a View of Reality in mathematical terms, and
neither view is actually reality, as Reality is not bound by our understanding of it. |
As I mentioned here and here, the classical world we observe is just an emergent property of the underlying quantum world, caused by a rapid loss of coherence in open
quantum systems via interactions with their environment. At the end of the day, classical mechanics is really nothing more than an approximation to
QM. The universe is ultimately quantum at its core--everything is governed by and can be explained by QM, both at the microscopic and macroscopic
scale. The reason we use classical mechanics for macroscopic systems is because it's equally accurate when it comes to large objects (see the
correspondence principle) only much simpler and easier to use.
What are at odds are QM and GR.
| Quote: |
So the tunnelling phenonenon is that with non-infinite bounds, the particle can actually be 'seen' at some point beyond those bounds, albeit rarely.
Is that right ? |
Correct. But whether or not it's "rarely" found beyond those bounds really just depends on how small the probability of finding it there is. This is
why the half-life of some radioactive elements (in the context of alpha decay) are longer or shorter than others. If the probability is extremely tiny
(i.e. a more stable nucleus), the half-life of the element will be longer and finding the alpha particle outside of a given nucleus would be somewhat
rare. On the other hand, if the probability is relatively high (i.e. a less stable nucleus), the half-life of the element will be much shorter,
meaning each individual atom is much more likely to decay at any given moment.
To kind of visualize what is going on, imagine the alpha particle rattling around inside the nucleus and every so often smashing into the
"containment" wall and then bouncing off. Now imagine that each time the alpha particle hits the wall, there's always a non-zero chance that it will
tunnel out of the nucleus and escape. Thus the higher the probability of that happening, the less time it's likely going to take.
[Edited on 8-24-2015 by Darkstar]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Thankyou for the clarifications - it is actually very helpful to have your input.
Appologies to yourself and blogfast for posting nonsense in such an informative thread that it should be stickied.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Hyperphysics gives a very nice explanation (much better than my finite potential analogy, actually) of alpha decay with QM tunnelling:
http://hyperphysics.phy-astr.gsu.edu/hbase/nuclear/alptun.ht...
Follow the links to see how alpha decay half-lives can be modelled with quantum mechanical tunnelling. Math included!
Quantum mechanics? What is it good for? ABSOLUTELY NOTHING!    
[Edited on 24-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So, to be clear, Classical physics says that the particle can never escape the bounds set, however observations show that it does escape, therefore
the Classical model simply does not work 100%.
QM allows for the escape, via the small, yet Finite Probability that the particle is seen escaping.
OK. If that's a fair precis of Quantum Tunelling, i may well be back on track.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
To put it maybe slightly more subtly, the Classical particle can only escape if it's energy is higher than the barrier potential
V<sub>b</sub>. If its energy (e.g. V<sub>1</sub>) is lower than the
barrier potential V<sub>b</sub>, the Classical particle is strictly confined to [-R,+R].
But for the Quantum particle, even if its energy is only V<sub>1</sub>, it can tunnel through the potential
barrier and has a small but finite and NON-ZERO probability to be found outside the Classical area [-R,+R].
The schematic below is for a one dimensional potential well with a potential energy function V(x) comparable to that of an alpha particle in a
nucleus:
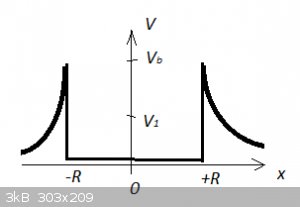
It might also be useful to remind us of the Correspondence Principle. As we make the system larger (larger and larger R) the system starts resembling
Classical mechanics: tunnelling decreases (until it ceases altogether), for instance. But for the alpha decay problem we are at extremely small scale:
femtometers!
[Edited on 25-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I suppose the notion that a Quantum Particle is never motionless is another key difference between classical and quantum theories.
In your diagram (ignoring wavefunctions for the moment) a moving particle with V1 will occasionally bounce off the precise point on the left hand
barrier to clear the right hand barrier, putting it outside the cell.
(right handed thinking)
Edit:
In essence the QM model takes dynamics into account to a degree.
[Edited on 25-8-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
A particle like an electron can be motionless but the particles we're interested in here, for our purposes in this course, are always
bound. Bound by a potential well, the nucleus of an atom or the nuclei of atoms (molecules, see later). And bound
particles have a ground energy that is ALWAYS non-zero. Non-zero ground energy means the particle has kinetic energy and thus that it moves
somehow.
It's tempting to imagine that movement in the 'Classical way' but that doesn't really work. For a particle in a 1D box with potential well (for
instance) we can calculate an expectation value (see quite a bit higher up) < v > for speed and it's zero (note that the expectation value is
only an average). But we know it moves because it has kinetic energy. Weird but true!
[Edited on 25-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Not weird at all in the agaspace model.
Still no maths yet relating to that, so pointless.
Hmm. Funny thing is that a dimentionless Point can't exists in agaspace.
Ignore all that. Back to the proper stuff.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Hydrogen Atom Wave Functions
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hydwf.htm...
Tick the boxes to change n.
The Radial wave functions R<sub>n,l</sub>(r) can also found here, scroll down for graphical representations of R and
R<sup>2</sup> (the probability functions).
http://quantummechanics.ucsd.edu/ph130a/130_notes/node233.ht...
Quantum numbers and Orbital naming
While the mathematical descriptions of hydrogen’s electron waves are referred to as the wave functions, their ‘physical’ manifestations are
called orbitals. Four main types of orbitals can be discerned: s, p, d and f:
n = 1, l = 0 === > 1s orbital
n = 2, l = 0 === > 2s orbital
n = 2, l = 1 === > 2p orbital
n = 3, l = 0 === > 3s orbital
n = 3, l = 1 === > 3p orbital
n = 3, l = 2 === > 3d orbital
n = 4, l = 0 === > 4s orbital
n = 4, l = 1 === > 4p orbital
n = 4, l = 2 === > 4d orbital
n = 4, l = 3 === > 4f orbital
As indicated above, for l > 0, m<sub>l</sub> = - l to + l. p, d and f type orbitals therefore have suborbitals:
p: l = 1, m<sub>l</sub> = - 1, 0, + 1. There are 3 types of p suborbitals.
d: l = 2, m<sub>l</sub> = - 2, - 1, 0, + 1, + 2. There are 5 types of d suborbitals.
f: l = 3, m<sub>l</sub> = - 3, - 2, - 1, 0, + 1, + 2, + 3. There are 7 types of f suborbitals.
To get a good idea of the shapes of these orbitals, I warmly recommend ‘Orbitron’ (a screen shot is attached below):
http://winter.group.shef.ac.uk/orbitron/AOs/1s/index.html
Play around with this to explore and suborbitals, and in the next instalment I will discuss these shapes a little more.
[Edited on 26-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So, Lunch has finished.
Where were we at ?
So far :-
QM model for particle in a 1 dimensional box.
Schrodinger's equation.
Mention of Eigenstates
Wavefunction encapsulates all of a particle's properties.
Quantum Tunelling.
QM used to plot electron orbital probabilities when expanded to 3D.
Is there a reason why the orbitals are not simply named a,b,c,d etc ?
[Edited on 1-9-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Instead of s,p,d and f? The latter letters were once used in spectroscopy to describe certain lines. s stands for "sharp", d for "diffuse", IIRW.
Today they're just symbols.
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Thanks. It's good to have some idea why stuff is labelled how it is.
So the Orbital thing.
Is this a plot of the probability of an electron existing in a space relatively close to the nucleus ?
First off, the s orbital.
I guess the two lobes are due to the +/- thing.
Edit:
I mean a plot of where the QM maths says it probably is if plotted over a very large number of values.
[Edited on 1-9-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
If you at look the shiny surfaces, for example for 2s, here:
http://winter.group.shef.ac.uk/orbitron/AOs/2p/index.html
Then the surface of the shape represents points for which the electron density for that orbital is the same - an isosurface. So in
this case the surface is for a 2s orbital with Ψ<sup>2</sup>(x,y,x) (the probability density, if you recall) set to a certain constant
value. This gives some idea of the shapes of the orbitals.
But orbitals are hard to imagine and are not made of shiny hard surfaces at all.
The "dots" representation is maybe more 'realistic', as it shows the orbital as 'fuzzy' shape, with no clear boundaries:
http://winter.group.shef.ac.uk/orbitron/AOs/2p/e-density-dot...
The colours represent the sign of the lobe and since as both Ψ and - Ψ are BOTH solutions to the SE, you can swap the colours over
and it's still the same orbital! But the sign does matter, as we'll see with Molecular Orbitals.
[Edited on 1-9-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK.
So the Orbital is a plot of the probability of finding an electron at, say n=1 given a number of variables, such as What ? When ?
If so, then the isosurface is an imagined nice smooth surface, imagining a convenient boundary so it can be all nice and shiny for the graphical
representation, whereas the reality is a fuzzy blob occupying approximately that shape.
A bit like a line drawing of a cat, omitting the furry bits.
|
|
|
| Pages:
1
..
6
7
8
9
10
..
33 |
|