| Pages:
1
..
5
6
7
8
9
..
33 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
ok. But never 750 for example, if the particle were pegged to the values that the two wavefunctions predict.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
AAHD:
With all due respect but you are sort of mudding the waters here a bit. We have been specifically keeping everything limited to particles in a
definite, say 'steady state', eigenstate, and not how a particle may transit from one eigenstate to another (e.g. n to m). The math of these
transitions is definitely outside the scope of this little excursion into QM/WM/QC...
Thanks nonetheless.
[Edited on 27-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
@AAND i appreciate your input : it is great to see commentary on stuff i barely grasp.
I suppose teach is right though, gotta see the Way first before walking, and Running is not an option just yet 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quantum physics has become a vast, vast paradigm. On holiday recently I read 'Quantum Mechanics - the theoretical minimum' by Leonard Susskind (&
Art Friedman) and had to study it rather than 'read' it.
To newcomers it must be a bewildering experience!
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | | ok. But never 750 for example, if the particle were pegged to the values that the two wavefunctions predict. |
That's right. One of the postulates of quantum mechanics is that when you measure an observable, the possible outcomes are the eigenvalues of the
corresponding operator. Here we're talking about energy, but the same applies to position, momentum, angular momentum, spin, charge, etc.
Also, quantum mechanics allows you to compute the probabilities of the various outcomes. In general the probabilities are functions of time, but not
when the observable (such as energy in an isolated system) is conserved.
Any other SF Bay chemists?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Woohoo !
Thanks AAHD. It appears as though i almost understood something !
Happy happy day !
I'll have another beer to celebrate.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The last in the series of properties of wave functions and some interim conclusions:
Parity of wave functions
In the case of a particle in a one dimensional box the coordinate system was chosen so that the box existed (U(x) = 0) between x = 0 and x = L. But
had we chosen the coordinate system so that U(x) = 0 for x = - L/2 to x = + L/2, the shapes of the resulting wave functions (and
eigenvalues E) would have been identical.
Note however that with the ‘new’ coordination system a centre of symmetry arises at x = 0 (at half the length of the box): looking to the left or
the right from that point the physical system looks the same. The wave function formula needs to be slightly adjusted to accommodate the new
coordination system, as:
Ψ<sub>n</sub>(x) = √(2/L) sin[nπ(x + L/2)/L]
It can be shown that:
Ψ<sup>*</sup>(x)Ψ(x) = Ψ<sup>*</sup>(-x)Ψ(-x)
Or for Real wave functions:
Ψ<sup>2</sup>(x) = ψ<sup>2</sup>(-x)
Thus the probability functions show symmetry with respect to x = 0, the point of symmetry. This can be generalized to the statement that wave
functions must have a definite parity with respect to symmetry operations in the physical problem, provided the potential energy function U(x)
of the system is also symmetric with respect to the symmetry centre. In math terms a function U(x) symmetrical to x = 0 means U(x) = U(-x).
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pfbox.htm...
An excellent and more mathematical explanation of Quantum parity can be found here:
http://physics.stackexchange.com/questions/13980/definite-pa...
Conclusions so far (particle in a one dimensional box)
• The Schrodinger equation is satisfied by suitable wave functions ψ and assorted eigenvalues E (the combination is also called an
‘Eigenstate’).
• The energies E are quantized and can be characterized by a quantum number n.
• The energy E cannot be exactly zero.
• The square of the wave functions are probability functions.
• The smaller the confinement, the larger the energy required.
• The wave functions are orthogonal.
• The wave functions show definite parity.
[Edited on 28-7-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Quote: Originally posted by aga  | so if a single particle can be described by two (or more) wavefunctions, then it cannot behave according to both functions at the same time ?
i.e. it's energy state will be defined by one wavefunction only, and never both at the same time. |
As AAHD explained, a particle can indeed behave according to more than one wave function at the same time. What you're getting at is essentially
what's called superposition.
For example, let's take the momentum basis. If the particle were in a definite momentum eigenstate, its momentum would be one of the possible
eigenvalues and its wave function would be the corresponding eigenfunction. On the other hand, if the particle were NOT in some definite momentum
eigenstate, then its momentum state is instead expressed as a superposition of all the possible momentum eigenstates. In other words, the
particle is basically in a sort of state where it has all possible momentum simultaneously. This is why you may sometimes hear people claim that
subatomic particles can "be in more than one location at the same time."
Now, if you were to actually attempt to measure/observe that particle's momentum, you would not find it in superposition. Instead, you would find it
in a single, definite eigenstate of momentum, which was selected randomly with some probability from the superposition of possible eigenvalues. This
is called wave function collapse.
Since Professor Blogfast is likely about to blow his top by now, you should probably get back to your main studies. Maybe a little later when he's not
looking we can see how all of this relates to Heisenberg's uncertainty principle! (i.e. the more momentum eigenstates in the superposition, the more
localized the particle's position becomes and the less defined its momentum gets, and vice-versa. thus the position state for a perfectly localized
particle would actually be a superposition of ALL values for momentum, from -∞ to ∞ and everything in between)
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Darkstar---precisely.
Any other SF Bay chemists?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Quote: Originally posted by Darkstar  | | if the particle were NOT in some definite momentum eigenstate, then its momentum state is instead expressed as a superposition of all the
possible momentum eigenstates. |
In effect, the maths are continually 'bent' to fit with observed phenomena.
That tends to suggest that the maths do not work.
I suspect there's a well-established counter argument.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
In effect, the maths are continually 'bent' to fit with observed phenomena.
That tends to suggest that the maths do not work.
I suspect there's a well-established counter argument. |
There would be but you need to be more precise about the 'bent math'.
What AAHD and Darkstar have been talking about hasn't actually been expressed in mathematical form here. What hasn't been rendered explicit
('precise', 'defined', 'unequivocal') yet cannot have been 'bent' yet.
[Edited on 28-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
True and i promised not to, until the end, so i won't.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Erratum – Probability and Probability Density
The functions (for a Pi1DB):
P<sub>n</sub>(x) = Ψ<ub>n</sub><sup>2</sup>(x) = (2/L) sin<sup>2</sup>(nπx/L)
... have previously been described erroneously as ‘probability functions’ when really they should have been described as 'probability
densities’ (also known as 'probability distribution', syn.). The difference is not mere semantics. Like an object can have a mass of 1 kg,
that same object can have a density many times higher than 1 kg/m<sup>3</sup>.
The previous assertion that P<sub>n</sub>(x) is the probability of finding the particle at position x is also wrong.
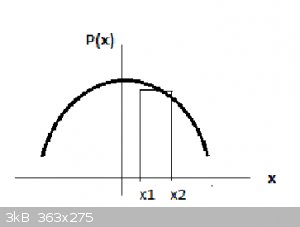
The actual probability of finding the particle can only be determined on an interval of x, for instance Δx = x<sub>2</sub> -
x<sub>1</sub> (see the attached schematic, below) and is then calculated from:
P(x<sub>2</sub> ,x<sub>1</sub> = ʃ
Ψ<sup>2</sup>(x)dx, integrated between x<sub>2</sub> and x<sub>1</sub> (for Real functionsΨ) = ʃ
Ψ<sup>2</sup>(x)dx, integrated between x<sub>2</sub> and x<sub>1</sub> (for Real functionsΨ)
For a relatively narrow interval Δx, P(x<sub>2</sub> ,x<sub>1</sub> is approximately the area of the rectangle in the schematic below, or: is approximately the area of the rectangle in the schematic below, or:
P(x<sub>2</sub>,x<sub>1</sub> ≈
Ψ<sup>2</sup>(x<sub>1,2</sub> ≈
Ψ<sup>2</sup>(x<sub>1,2</sub> Δx (assuming that
Ψ<sup>2</sup>(x<sub>1</sub> Δx (assuming that
Ψ<sup>2</sup>(x<sub>1</sub> ≈
Ψ<sup>2</sup>(x<sub>2</sub> ≈
Ψ<sup>2</sup>(x<sub>2</sub> ) )
For systems involving electrons the probability density is is often referred to as the electron density (we’ll encounter that term
frequently in the future). In areas where the electron density (Ψ<sup>2</sup> is high, the probability of finding electrons is high. is high, the probability of finding electrons is high.
Apologies for the error!
[Edited on 29-7-2015 by blogfast25]
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
If anyone's interested, I made a table of contents to make navigating a little easier. The larger this thread gets, the more scattered the information
will become and the harder it'll be to find specific things. This thread already has over 160 posts, and I imagine (and hope) it will continue to grow
over the years. With a table of contents, readers will be able to quickly locate the topic(s) they are interested in learning more about without
having to sort through page after page to find it. Hopefully this will make the thread slightly less intimidating for newcomers. (as if the material
wasn't already intimidating enough!)
If it's alright with blogfast, maybe a moderator can add this to the first post? We can update it periodically as needed.
*NOTE* - Fixed it so that it works no matter what your "posts per page" is set to. I suggest all future additions be done
this way as well. Don't copy the link to a post out of your actual address bar as it has a reference to the page it is on, which will vary from user
to user depending on their settings. Instead, hover over the "posted on..." link above the target post and just copy that link directly.
Quick Navigation
Part I – Basic Wave Mechanics
Additional Contributions
[Edited on 7-30-2015 by Darkstar]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
That is very useful Darkstar, thank you very much! 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Before we start discussing the hydrogen atom, let’s have a look at another ‘simple’ QS for bound particles.
The Quantum Harmonic Oscillator
The Quantum Harmonic Oscillator (QHO) is an approximation of vibrational modes of a diatomic molecule like H<sub>2</sub> or HCl. Unlike in
the example of a Pi1PD, U(x), the potential energy function, is not zero, but it is symmetric (with respect to x = 0).
General outline:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc.html...
Wave functions and probability densities:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc5.htm...
Note that there is a finite probability that the oscillator will be found outside the "potential well" indicated by the smooth curve. This is
forbidden in Classical physics. It’s a phenomenon called ‘Quantum tunneling’.
Eigenvalues E:
E<sub>n</sub> = (n + ½) ω ћ
(With ћ = h/(2π) (“h bar”) and n the Quantum Number of the QHO)
Note that here n = 0 is allowed because E<sub>0</sub> = ½ ω ћ, that is non-zero.
Ψ<sub>0</sub> is also non-zero and thus a Real solution to the SE.
Application: the Vibration/rotation spectrum of HCl
The absorption spectrum of HCl:
http://hyperphysics.phy-astr.gsu.edu/hbase/molecule/vibrot2....
The central gap is due to the transition n = 0 to n = 1 for the HQO that is HCl. The other equidistant peaks are due to HCl also being a Quantum
Rotator.
[Edited on 1-8-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Operators: Classic and Quantum
(All in one dimension (x))
For Classical systems the system's properties are defined as follows.
Classical:
Position = x
Velocity: v<sub>x</sub> = dx/dt
Momentum: p<sub>x</sub> = mv<sub>x</sub> = m dx/dt
Kinetic energy: E = 1/2 mv<sup>2</sup>
Total energy: E = 1/2 mv<sup>2</sup> + U
Quantum:
Very high up in this course I wrote:
| Quote: | | The wave function ψ contains all measurable information about the particle. |
There exist a number of relationships (which won’t be derived here) that allow to ‘extract’ that measurable information from the wave function.
(Time independent, x dimension)
Velocity: v = p/m = - (iћ/m) δψ(x)/δx
Momentum: p = - iћ δψ(x)/δx
Kinetic energy: - (iћ<sup>2</sup>/2m) δ<sup>2</sup>ψ(x)/δx<sup>2</sup>
Total energy: - (iћ<sup>2</sup>/2m) δ<sup>2</sup>ψ(x)/δx<sup>2</sup> + U(x)ψ(x)
If we define an Operator as a mathematical operation we apply to the wave function, then we can define the following Quantum Operators (operators are
noted in bold and italic here):
Quantum Momentum operator p = - iћ δ/δx
Quantum Velocity operator v = p/m
Hamiltonian operator (total energy) H = - (iћ<sup>2</sup>/2m)
δ<sup>2</sup>/δx<sup>2</sup> + U(x)
The time-independent Schrodinger Equation can thus be re-written as:
Hψ = Eψ
... with ψ an eigenfunction and E an eigenvalue.
For a general Quantum operator Q:
Qψ = qψ
... with ψ an eigenfunction and q an eigenvalue.
So, observable information about the QS can be obtained by applying quantum operators to the wave function ψ.
Expectation Values:
Position expectation value:
The expectation value < x > can be interpreted as the average value of x that we would expect to obtain from a large number of measurements.
Alternatively it could be viewed as the average value of position for a large number of particles which are described by the same wave function.
< x > = ʃ ψ<sup>*</sup>x ψdx, integrated over - ∞ to +∞
For Real wave functions:
< x > = ʃ xψ<sup>2</sup>dx, integrated over - ∞ to +∞
For the Pi1DB (infinite potential well):
< x > = L/2. The average of many position measurements yields L/2.
For momentum, the expectation value is:
< p > = ʃ ψ<sup>*</sup>pψdx, integrated over - ∞ to +∞
With p the Quantum momentum operator.
For Real wave functions:
< p > = ʃ ψpψdx, integrated over - ∞ to +∞
It can be shown that for eigenstates (of bound particles), < p > = 0. And because < p > = m< v >, the expectation value < v >
= 0 also.
Does this mean that the particle is motionless? No, not all. Take the example of a Pi1DB. The particle is analogous to a prisoner in
a cell: the prisoner can move about in the confined space of the cell but he’s not going anywhere. His average velocity is effectively 0. If for the
Pi1DB < v > > 0 then the particle would effectively be escaping, so < v > = 0 is the ‘natural’ result.
[Edited on 3-8-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Woah !
Hang on a sec Blogfast.
Give us at least time to read the blackboard, please !
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Did you perhaps miss the one but last session?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Yep.
(blush)
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
No worries. You'll have plenty of tellyless evenings to figure it all out!  You
know: '999 channels and never anything on' and all that... You
know: '999 channels and never anything on' and all that...
|
|
|
Darkstar
Hazard to Others
  
Posts: 279
Registered: 23-11-2014
Member Is Offline
Mood: Sleepy
|
|
Perhaps he can make up for it by correctly answering the following, which will serve as extra credit. All students are welcome (and encouraged) to
try, of course, so please don't hesitate if you think you know the answer. All I ask is that you don't cheat and look it up! Also, I would appreciate
it if the more knowledgeable readers would remain silent. Let the beginners figure this one out.
Quote: Originally posted by blogfast25  | | Note that there is a finite probability that the oscillator will be found outside the "potential well" indicated by the smooth curve. This is
forbidden in Classical physics. It’s a phenomenon called ‘Quantum tunneling’. |
Consider for a moment how exactly this phenomenon, known as "quantum tunneling," could be applied to chemistry, particularly radioactivity and the
radioactive decay of elements with unstable nuclei. For our purposes, let's consider only the decay process known as alpha decay, a form of cluster
decay where a nucleus emits an alpha particle (two protons and two neutrons--basically a helium nucleus). This decay process is ultimately the result
of a Coulomb repulsion between the alpha particle and the rest of the nucleus, both being positively-charged, that pushes the two away from one
another. The problem, however, is that at the short distances we're dealing with, the attraction caused by the strong force completely overpowers any
electromagnetic repulsion between the alpha particle and the rest of the nucleus. This creates a potential well that effectively traps the alpha
particle.
So here's the question: If the alpha particle is initially trapped inside the nucleus and forbidden to escape, similar to how the particle in
the box is trapped and forbidden to escape, how is it that the alpha particle is eventually able to overcome the strong force and leave the potential
well, all without ever actually having enough energy to escape the nucleus in any classical sense? In other words, how might quantum tunneling be used
to explain this?
Hint: Unlike the particle in the box, the potential well the alpha particle is trapped in has finite potential walls. Now recall
wave-particle duality and Heisenberg's uncertainty principle.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by Darkstar  |
Hint: Unlike the particle in the box, the potential well the alpha particle is trapped in has finite potential walls. Now recall
wave-particle duality and Heisenberg's uncertainty principle.
|
Darkstar:
Would you consider authoring a small segment on the Uncertainty Principle? Perhaps one that relates confinement energy to well size? As we know
confinement energy is more or less inversely proportional to well size.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Last stop before the hydrogen atom. Darkstar should feel free to add other examples of the uncertainty principle.
The Uncertainty Principle
The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. There is a minimum for the product of the
uncertainties of these two measurements. There is likewise a minimum for the product of the uncertainties of the energy and time.
σ<sub>x</sub> σ<sub>p</sub> > ћ/2
σ<sub>t</sub> σ<sub>E</sub> > ћ/2
This is not a statement about the inaccuracy of measurement instruments, nor a reflection on the quality of experimental methods; it arises from the
wave properties inherent in the quantum mechanical description of nature. Even with perfect instruments and technique, the uncertainty is inherent in
the nature of things.
σ<sub>x</sub>, σ<sub>p</sub>, σ<sub>t</sub> and σ<sub>E</sub> are standard deviations. The smaller
σ is, the more accurately the property (x, p, t or E) is known.
Application to a Pi1DB:
Higher up we saw that the confinement energy of a bound particle increases as the size of the box decreases. We can show this to be the direct
consequence of the Uncertainty Principle.
For a particle in a box x = 0 to x = L it can be shown that:
σ<sub>x</sub> = L/√12
(Proof: http://hyperphysics.phy-astr.gsu.edu/hbase/math/stdev.html#c...)
With the uncertainty principle:
σ<sub>p</sub> > ћ/(2 σ<sub>x</sub> = ћ√12/2L = ћ√12/2L
It can also be shown that σ<sub>p</sub><sup>2</sup> = < p<sup>2</sup> >
The minimum kinetic energy (KE) for confinement is thus:
< KE<sub>min</sub> > = < p<sup>2</sup> >/2m
Reworked we get:
< KE<sub>min</sub> > = 3 ћ<sup>2</sup>/(2mL<sup>2</sup>
Or: < KE<sub>min</sub> > = 3 h<sup>2</sup>/(8π<sup>2</sup>mL<sup>2</sup>
E<sub>1</sub> = h<sup>2</sup>/(8mL<sup>2</sup>
This means effectively that E<sub>1</sub> > < KE<sub>min</sub> > ("the ground state energy is larger
than the minimum kinetic energy demanded by the Uncertainty Principle").
So this means that the calculated eigenvalue E<sub>1</sub> (ground state) is in agreement with the Uncertainty Principle. By contrast, a
ground state of E<sub>1</sub> = 0 would be in flagrant violation of it.
Further reading: on the page below the author(s) calculate the ground state of the hydrogen atom using nothing more than the
Uncertainty Principle!
http://quantummechanics.ucsd.edu/ph130a/130_notes/node98.htm...
[Edited on 8-8-2015 by blogfast25]
|
|
|
Dan Vizine
National Hazard
   
Posts: 628
Registered: 4-4-2014
Location: Tonawanda, New York
Member Is Offline
Mood: High Resistance
|
|
I'll be happy if I finally understand Hamiltonian operators....you've got my interest!
"All Your Children Are Poor Unfortunate Victims of Lies You Believe, a Plague Upon Your Ignorance that Keeps the Youth from the Truth They
Deserve"...F. Zappa
|
|
|
| Pages:
1
..
5
6
7
8
9
..
33 |