| Pages:
1
..
4
5
6
7
8
..
33 |
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Hardly likely that there will be another agajunior.
Age, surgery and good sense ensure that.
Aga's Owner, Agaitas and Hounds/beasts in general plus Beer are the main distractants.
Edit:
Apologies for asking a question to which you already explaned the answer to earlier in the thread.
[Edited on 24-7-2015 by aga]
[Edited on 24-7-2015 by aga]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Apologies for asking a question to which you already explaned the answer to earlier in the thread.
|
Try keeping that dementia in check!
Wot was we talking about again? Totally gone... 
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
I think we were looking for a Quantum of Solace, which i found under the sofa along with a fossilised bit of cake.
Cake. Mmm Cake. Cake is nice.
I'll put the kettle on.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
You boil your beer? You only need to do that before fermentation, you know?
Next instalment on the morrow. The cliffhanger continues!
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
QMSMers who have ever dropped a few grains of kitchen salt into a hot flame (or watched their potatoes boil over!) will have seen how that colours the
flame strongly yellow. This is due to emission of photons from excited electrons in the sodium atoms of the NaCl, returning to the ground state. Other
elements emit other colours, see ‘flame tests’. I’ll briefly illustrate how emission spectra work using our particle in a 1D box.
Emission Spectrum of a particle in a one dimensional box (Pi1DB)
When a particle in a one dimensional box is in an excited state (n > 1) it can ‘fall’ back to a lower state, for example from
n<sub>2</sub> to n<sub>1</sub> (with n<sub>2</sub> > n<sub>1</sub> and energy will be emitted: ΔE = E<sub>n1</sub> -
E<sub>n2</sub> < 0. and energy will be emitted: ΔE = E<sub>n1</sub> -
E<sub>n2</sub> < 0.
Quick side note: the mechanics of such transitions (from n<sub>2</sub> to n<sub>1</sub> and their probabilities are described by the Time Dependent Schrodinger Equation and
will not be treated here. and their probabilities are described by the Time Dependent Schrodinger Equation and
will not be treated here.
Assuming the particle is an actual electron, the energy emission is in the form of a photon (electromagnetic radiation like light, X-rays, IR or UV)
with energy E = hf.
Thus hf = ΔE
This schematic should be useful (emission AND absorption):
http://hyperphysics.phy-astr.gsu.edu/hbase/mod5.html#c2
Spectroscopically, the transitions (and corresponding photon emissions), are often organised in ‘series’. Here, somewhat arguably, we can discern
Series 1, 2, 3 etc by setting n<sub>1</sub> to 1, 2, 3 etc.
The frequencies f for a photons emitted in Series 1 then become:
f<sub>1</sub> = h/(8mL<sup>2</sup> -
h/(8mL<sup>2</sup> -
h/(8mL<sup>2</sup> n<sub>2</sub><sup>2</sup> n<sub>2</sub><sup>2</sup>
= h/(8mL<sup>2</sup> [1 -
n<sub>2</sub><sup>2</sup>] [1 -
n<sub>2</sub><sup>2</sup>]
For Series 2:
f<sub>2</sub> = h/(8mL<sup>2</sup> [4 -
n<sub>2</sub><sup>2</sup>] [4 -
n<sub>2</sub><sup>2</sup>]
For Series n:
f<sub>2</sub> = h/(8mL<sup>2</sup> [n<sup>2</sup> - n<sub>2</sub><sup>2</sup>] [n<sup>2</sup> - n<sub>2</sub><sup>2</sup>]
Of course h/(8mL<sup>2</sup> =
E<sub>1</sub>. =
E<sub>1</sub>.
Note also that for emitted photons c = λf (c = speed of light, λ = wavelength of photon, f = frequency of photon), so that f can be converted to λ
easily.
A calculated emission spectrum of a Pi1DB, for a ground state of E<sub>1</sub> = 6.8 eV is shown below.
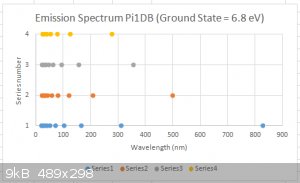
[Edited on 25-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So, let me get that straight ... if you can accurately measure the wavelength of the radiation from a system collapsing from one energy state to
another, you can calculate the E values of all levels ?
How can you determine what the state change is in the first place ?
i.e is it going n5 to n4 or n5 to n1 ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | So, let me get that straight ... if you can accurately measure the wavelength of the radiation from a system collapsing from one energy state to
another, you can calculate the E values of all levels ?
|
You would always need to know (or guess) the form of the energy function, say E<sub>n</sub> =
F(E<sub>1</sub>,n) ("E<sub>n</sub> a function of E<sub>1</sub> and n"), as well as one of the n numbers in:
ΔE = E<sub>n1</sub> - E<sub>n2</sub> (= hf)
The ground state of the hydrogen atom had been determined by spectroscopy, some years before Schrodinger solved the SE for the H atom.
In the case of a Pi1DB, the difference between two adjacent energy levels n and n+1 is always:
ΔE = E<sub>1</sub>(n+1)<sup>2</sup> –E<sub>1</sub>n<sup>2</sup>
= E<sub>1</sub>(n<sup>2</sup> + 2n + 1 – n<sup>2</sup>
= E<sub>1</sub>(2n+1)
This kind of expression can be useful for a spectrocopist to determine E<sub>1</sub> with.
[Edited on 26-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Deduce the working of the universe and the Energy of a particle by maths and the colour ?
That is truly remarkable.
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
The 'magik' of science! 
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Next instalment:
Normalisation of Wave Functions (Pi1DB)
Note that the wave functions discussed above have already been normalised but I want to briefly expand on the so-called Normalisation Requirement
separately.
As we know, ψ(x)<sup>2</sup> represents the probability P(x) of finding the particle in the location x.
We also know that the particle in a one dimensional box is always found inside the box (as it cannot escape from it due to the infinitely high
potential energy) and the boundaries x = 0 and x = L.
In mathematical terms that means that to sum total of all values of P(x) over the interval [x = 0, x = L] must be 1, as this represents the
probability of finding the particle inside the box. In mathematical terms this means:
Σ P(x) = Σ ψ(x)<sup>2</sup> = 1, summation over all values of x.
Because ψ(x), and thus by extension also ψ(x)<sup>2</sup>, is a smooth and continuous function, the summation Σ is replaced by
integration:
∫ψ(x)<sup>2</sup>dx = 1, integrated between x = 0 and x = L.
In the following example:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pbox.html...
… the normalisation requirement is used to determine the factor A (for ‘amplitude’ of the wave function) to be √(2/L). This guarantees that
the resulting wave functions:
Ψ<sub>n</sub>(x) = √(2/L) sin(nπx/L)
… and the resulting probability functions return the correct values.
Note that in the given example, A<sup>2</sup> = 2/L, has two roots:
A<sup>+</sup> = + √(2/L) and A<sup>-</sup> = - √(2/L)
And indeed both +ψ and –ψ both satisfy the SE. Textbooks sometimes note the wave functions as +/- ψ. The
probability functions ψ<sup>2</sup> are not affected by the sign either, of course.
The normalisation ‘procedure’ needs to be applied to all wave functions of bound particles, in all quantum systems. The
mathematics of the procedure depends a lot on the QS in question.
[Edited on 26-7-2015 by blogfast25]
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | So, let me get that straight ... if you can accurately measure the wavelength of the radiation from a system collapsing from one energy state to
another, you can calculate the E values of all levels ?
How can you determine what the state change is in the first place ?
i.e is it going n5 to n4 or n5 to n1 ? |
The wavelength of the spectral line gives the difference in energies between the two states. Different spectral lines correspond to different pairs
of states. For example, there is one spectral line on going from E2 to E1, another from E3 to E1, another from E3 to E2, etc. It's possible to
disentangle this information and to get the energy levels themselves, up to an arbitrary choice for one specific level. For example, if you just
choose E1=0, then you can use the spectral information to find all the other levels. You don't need a formula for the energy levels to do this.
Actually the process can be more complicated, because some transitions between some pairs of levels are very weak, or almost not present. That is,
one must work with partial information.
Before the advent of quantum mechanics spectroscopists had figured out that the frequencies of spectral lines could be expressed as the differences of
a smaller set of frequencies, what we now know are the energy levels (converting energy to frequency by E=hf). The energy levels themselves didn't
seem to follow any simple mathematical pattern, with the exception of hydrogen, where Balmer found the formula f =
k(1/n<sub>1</sub><sup>2</sup> - 1/n<sub>2</sub><sup>2</sup> for the frequencies of the spectral lines, where k is a constant. We now understand this by saying that
E<sub>n</sub> = -k/n<sup>2</sup> are the energy levels of hydrogen. for the frequencies of the spectral lines, where k is a constant. We now understand this by saying that
E<sub>n</sub> = -k/n<sup>2</sup> are the energy levels of hydrogen.
Any other SF Bay chemists?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Incredible !
So if the spectrum emitted by a system (determined experimentally) coincides with the calculated En values with no ouliers), that's kind of
a proof that the assumptions of QM are correct, and that matter does in fact obey those laws ?
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Yes, getting the spectrum right was one of the main objects in the early history of quantum mechanics. The first major triumph in this regard was
Bohr's theory of 1911 (thereabouts) which derived the Balmer formula for hydrogen from some assumptions about quantized classical orbits. Bohr's
method however did not work for helium or any other atom, that required the full quantum mechanics of Schro"dinger and Heisenberg and didn't come
until 1927 (thereabouts). By examining spectroscopic data, theorists discovered electron spin and the exclusion principle, they explained the fine
structure of atomic spectra as relativistic corrections, etc etc.
Any other SF Bay chemists?
|
|
|
Magpie
lab constructor
    
Posts: 5939
Registered: 1-11-2003
Location: USA
Member Is Offline
Mood: Chemistry: the subtle science.
|
|
Can electron spin be described in classical terms? If not, what is it other than -1/2 or +1/2?
The single most important condition for a successful synthesis is good mixing - Nicodem
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
The existence of spin was never suspected before quantum mechanics came along, and it's usually regarded as a fundamentally quantum phenomenon, with
no classical analog. Sometimes it is said that classical mechanics becomes valid when quantum numbers are large, and spin (electron spin, anyway) has
a quantum number that never goes above 1/2. So in that respect you'd have to say that it is purely quantum mechanical.
Nevertheless there are classical models that capture some of the features of quantum spin. A very crude one is to imagine that the electron is a
charged sphere, spinning on an axis. Because the rotation carries the charge around in circles, it creates a magnetic field. It is the electron's
magnetic field that allows spin to be detected and measured. Whatever the model, it is a fact that an electron has both an electric field and a
magnetic field.
Any other SF Bay chemists?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
So if in QM, a particle cannot have an energy state other then 1,2,3 etc, how come it needs to be 'bent' to make a 0.5 state ?
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
I don't know what you mean by "bent", or what a 0.5 state is. Please explain.
Any other SF Bay chemists?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
aga, re, the 'spin' of an electron, it's something that you just kind of have to accept.
| Quote: | | In quantum mechanics, the spin–statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its
intrinsic angular momentum (that is, the contribution to the total angular momentum that is not due to the orbital motion of the particle). All
particles[citation needed] have either integer spin or half-integer spin (in units of the reduced Planck constant ħ). |
https://en.wikipedia.org/wiki/Spin%E2%80%93statistics_theore...
Electrons have an intrinsic (regardless of physical system they find themselves contained in) Spin Quantum Number, m<sub>s</sub> = - ½
or + ½. So simply consider an electron to be a Quantum System with only two allowed Quantum States.
Spin was discovered in the Stern Gerlach Experiment:
https://en.wikipedia.org/wiki/Stern%E2%80%93Gerlach_experime...
[Edited on 27-7-2015 by blogfast25]
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
I hope people don’t mind too much but I want to push on, as there is still a lot of material to cover. With this instalment we’re past about 75 %
of Part 1.
Thank you for reading so far.
Wave function orthogonality
Two mathematical functions f(x) and g(x) are said to be orthogonal on an interval a <= x <= b, if:
∫f(x)g(x)dx = 0 (integrated between x = a and x = b)
Take two wave functions (of the Pi1DB) with differing energy levels:
Ψ<sub>n</sub>(x) = √(2/L) sin(nπx/L)
Ψ<sub>m</sub>(x) = √(2/L) sin(mπx/L)
Provided n is not equal to m (remember that both n and m are positive, non-zero integers!) the energy levels (the eigenvalues
associated with these wave functions) are not the same.
It can be proved that:
∫ √(2/L) sin(nπx/L) √(2/L) sin(mπx/L) dx = 0 (integrated between x = 0 and x = L), because:
∫sin(nπx/L) sin(mπx/L) dx = 0 (integrated between x = 0 and x = L)
(The proof can be found here: http://tutorial.math.lamar.edu/Classes/DE/PeriodicOrthogonal...)
This means that for the particle in a one dimensional box two non-equal wave functions are always orthogonal. It turns out that this
is the case for all wave functions of bound particles. The physical interpretation of this is that the particle can be in the eigenstate associated
with n (having eigenvalue E<sub>n</sub> or with m (having eigenvalue
E<sub>m</sub> or with m (having eigenvalue
E<sub>m</sub> but not in both states at once. Of all the
possible states n = 1, 2, 3,… the system can only be in one eigenstate at a given moment t. but not in both states at once. Of all the
possible states n = 1, 2, 3,… the system can only be in one eigenstate at a given moment t.
And this has also consequences for quantum chemistry, folks!
[Edited on 27-7-2015 by blogfast25]
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
Thank You for posting so far, and not giving up the will to live !
Looking up what Orthogonal means, i'm still a bit confused.
Does this mean that say two particles with differing wave functions cannot occupy the same energy level at the same time ?
... or that a single particle can be described by two different wave functions ?
|
|
|
blogfast25
International Hazard
    
Posts: 10562
Registered: 3-2-2008
Location: Neverland
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  |
Thank You for posting so far, and not giving up the will to live !
Looking up what Orthogonal means, i'm still a bit confused.
... or that a single particle can be described by two different wave functions ? |
The meaning of words depends enormously on context. I don't know what you've been looking up.
A single particle can have a whole bunch of wave functions ψ and assorted eigenvalues E but it can only be in ONE of these eigenstates at once. This
may sound self-evident but the orthogonality property proves this.
Forget about multi-particle systems for now, they'll come out of your ears in Part 2!
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
so if a single particle can be described by two (or more) wavefunctions, then it cannot behave according to both functions at the same time ?
i.e. it's energy state will be defined by one wavefunction only, and never both at the same time.
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | so if a single particle can be described by two (or more) wavefunctions, then it cannot behave according to both functions at the same time ?
i.e. it's energy state will be defined by one wavefunction only, and never both at the same time. |
If a particle is in a state of definite energy, then the energy must be one of the eigenvalues E<sub>n</sub>, and the wave function is the
corresponding eigenfunction psi<sub>n</sub>. In this case the probability of finding the particle in any region of space is constant in
time, and if you measure the energy you always get the value E<sub>n</sub>.
But a particle need not have a definite energy, just as it need not have a definite position or momentum. A particle can be in a linear combination
of two energy eigenstates, for example, its wave function could be c<sub>1</sub> psi<sub>1</sub> + c<sub>2</sub>
psi<sub>2</sub>,
where c<sub>1</sub> and c<sub>2</sub> are two complex numbers whose squares add to 1. In that case the probability of
measuring the energy and finding E<sub>1</sub> is |c<sub>1</sub>|<sup>2</sup>, and that of finding
E<sub>2</sub> is |c<sub>2</sub>|<sup>2</sup>.
These probabilities are independent of time. But the probability of finding the particle in a given region of space is now a function of time.
The most general state of the system is a linear combination of all the energy eigenfunctions. In this way the particle can behave like all the
energy eigenfunctions all at once.
Such states can be created by optical pumping, in which an system in its ground state is lifted into an excited state. While this is going on, the
system is in a linear combination of the ground state and the excited state. The reverse happens when a state decays; during the decay process the
wave function is a linear combination of the excited state and the target state (a state of lower energy).
Another way to do this is to take a system in a definite energy state, and then change the Hamiltonian, for example, by turning on an electric or
magnetic field. The poor system, which was happily in an eigenstate of the old Hamiltonian, suddenly finds that the Hamiltonian and its eigenstates
have changed, so it is no longer in an energy eigenstate of the new Hamiltonian.
Any other SF Bay chemists?
|
|
|
aga
Forum Drunkard
    
Posts: 7030
Registered: 25-3-2014
Member Is Offline
|
|
OK. So if a particle behaves according to two or more wavefunctions, let's say with products En being 10, 100 and 1000 for n=1,2,3
and Em products being 5, 500 and 1500 eV, then all you're saying is that it will never be at 100 and 1500 eV at the same time.
Or something like that. Kinda makes sense.
|
|
|
annaandherdad
Hazard to Others
  
Posts: 387
Registered: 17-9-2011
Member Is Offline
Mood: No Mood
|
|
Quote: Originally posted by aga  | OK. So if a particle behaves according to two or more wavefunctions, let's say with products En being 10, 100 and 1000 for n=1,2,3
and Em products being 5, 500 and 1500 eV, then all you're saying is that it will never be at 100 and 1500 eV at the same time.
|
Not sure what you mean by products. If 100 and 1500 are two energy levels (in some units) then the system can certainly be in a linear combination
of the two corresponding wave functions (that is, energy eigenfunctions). If it were, and you made a measurement of energy, you'd get 100 with some
probability, and 1500 with some other probability.
Any other SF Bay chemists?
|
|
|
| Pages:
1
..
4
5
6
7
8
..
33 |