I decided to bypass full normalisation and replace it with numerical normalisation (integrating the functions y<sup>2</sup> by means of a
spread sheet, used also for the plots).
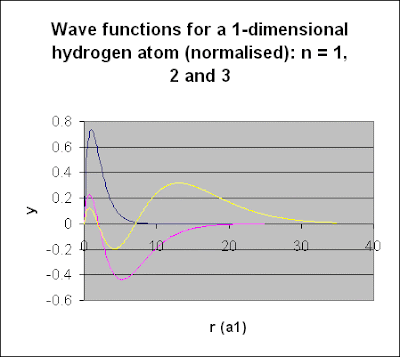
Below are the normalised wave functions obtained that way, with α<sub>1</sub> = ½ (2π
e<sup>2</sup>m/hε<sub>0</sub> <sup>3/2</sup> (e = charge of the electron, m = mass of the electron, h = Planck’s constant, ε<sub>0</sub> = vacuum
permittivity) - ground state and 1st and 2nd excitations: <sup>3/2</sup> (e = charge of the electron, m = mass of the electron, h = Planck’s constant, ε<sub>0</sub> = vacuum
permittivity) - ground state and 1st and 2nd excitations:
The electron densities:
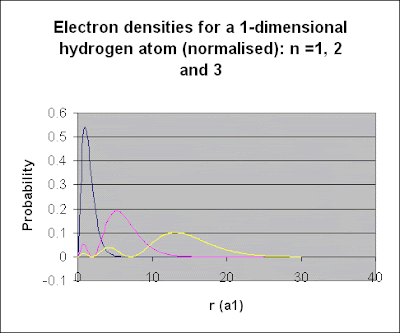
Note how the second and third 'lobes' are always higher than the first one.
[Edited on 18-4-2011 by blogfast25]
|