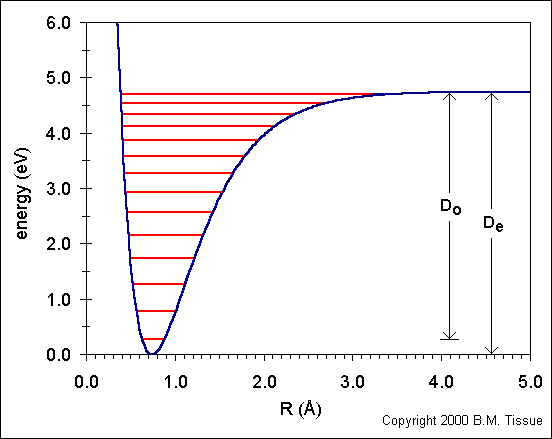
| Both in quantum mechanics and chemical thermodynamics the ZPE is derived from ideal systems in the gas phase, with no interaction between the
particles. There's a type of enthalpy in chemical thermodynamics which is also defined as 0K in the gas phase, but I can't remember which one.
|